Die Physik beschreibt im Allgemeinen Naturphänomene und die statistische Physik ist ein Zweig der Physik, der Methoden und Wahrscheinlichkeitsrechnungen nutzt, um physikalische Systeme zu beschreiben.
Statistische Berechnungen helfen dabei, Phänomene als Ganzes und nicht im Einzelnen zu beschreiben. So geht es beispielsweise nicht um die Bewegung eines einzelnen Teilchens, sondern um das Phänomen der Teilchenbewegung als Ganzes.
In diesem Artikel erklären wir dir, was genau die statistische Physik ist und in welchen Teilbereichen sie wichtig ist.

Was ist statistische Physik?
Als Zweig der physikalischen Disziplin befasst sich die statistische Physik mit den Methoden der Wahrscheinlichkeitstheorie, die zur Beschreibung physikalischer Systeme genutzt werden können. So können Forscher Aussagen über die Eigenschaften und das Verhalten eines großen zusammengesetzten Systems machen.
Grundsätzlich unterscheidet man in der Physik zwischen Makrozustand und Mikrozustand. Der Mikrozustand beschreibt die mikroskopischen Geschehnisse eines Systems, während es im Makrozustand um die Gesamtheit des Systems geht.
Und mit diesen Makrosysteme beschäftigt sich die physikalische Statistik, ohne dass das Verhalten der einzelnen Teile in diesem System eine Rolle spielen. Der Fokus liegt auf dem Makrozustand in einem System und die gewonnenen Theorien liefern Erkenntnisse für das Verhalten eines komplexen zusammengesetzten Systems.
✅ Wettervorhersage: Meteorologen nutzen chaostheoretische und statistische Modelle, um Klimatrends und Unwetter vorherzusagen.
✅ Materialwissenschaft: Die Wärmeleitfähigkeit, elektrische Eigenschaften und mechanische Stabilität von Materialien werden mit statistischen Methoden berechnet.
✅ Wirtschaftsphysik (Ökonophysik): Statistische Modelle helfen, Börsenkurse und Finanzmärkte zu analysieren.
✅ Neurowissenschaften: Die Aktivitätsmuster von Neuronen können mit statistischen Netzwerken beschrieben werden.
✅ Verkehrsfluss-Analysen: Vorhersagen über Staus basieren auf statistischen Mechaniken, ähnlich wie bei Teilchenbewegungen in einem Gas.
Damit eine solche Theorie über das Verhalten mehrerer Teilchen zustande kommt, versucht die statistische Physik auf mathematischer Basis Sätze aus der Wahrscheinlichkeitstheorie auf ein beobachtbares Phänomen anzuwenden.
Statistische Verfahren und Berechnungen werden genutzt, wenn eine beobachtbare Größe in einem System von den Eigenschaften und Verhaltensweisen der Teilsysteme abhängig ist.
Die durch die statistischen Berechnungen getätigten Aussagen haben den Charakter von Wahrscheinlichkeiten, die aber mit steigender Anzahl der Teile des Systems immer mehr zu Gewissheiten werden.
Auch die theoretische Physik bedient sich statistischer Berechnungen.
Die Geschichte der statistischen Physik
Die statistische Physik entwickelte sich aus der Wärmelehre und der kinetischen Gastheorie. Ihre Ursprünge reichen bis ins 17. und 18. Jahrhundert zurück, als Wissenschaftler erstmals versuchten, die thermischen Eigenschaften von Gasen mit mechanischen Gesetzen zu erklären.
1738
Kinetische Gastheorie
Daniel Bernoulli veröffentlicht seine kinetische Gastheorie.
1860
Geschwindigkeitsverteilung der Moleküle
James Clerk Maxwell formuliert die Geschwindigkeitsverteilung der Moleküle.
1872
H-Theorem
Ludwig Boltzmann entwickelt das H-Theorem zur Erklärung des thermodynamischen Gleichgewichts.
1884
Konzept des statistischen Gleichgewichts
Boltzmann definiert das Konzept des statistischen Gleichgewichts.
1900
Strahlungsformel
Max Planck leitet die Strahlungsformel her und legt den Grundstein der Quantenmechanik.
1905
Brownsche Bewegung
Albert Einstein erklärt die Brownsche Bewegung und stärkt die atomistische Theorie.
1920er
Fermi-Dirac- und Bose-Einstein-Statistiken
Fermi-Dirac- und Bose-Einstein-Statistiken werden entwickelt.
1960er-1980er
Einführung numerischer Methoden
Einführung numerischer Methoden wie Monte-Carlo-Simulationen und Molekulardynamik.
Heute
Anwendung
Anwendung statistischer Methoden in Quantenmechanik, Biophysik und Materialwissenschaften.
Besonders im 19. Jahrhundert führten bahnbrechende Entdeckungen dazu, dass statistische Methoden einen festen Platz in der Physik einnahmen. Heute bildet die statistische Physik die Grundlage für viele moderne Forschungsbereiche, von der Thermodynamik über die Quantenmechanik bis hin zur Computerphysik.
Brauchst du online Nachhilfe Physik?
Die Anfänge: Mechanische Theorie der Wärme
Im 17. und 18. Jahrhundert entwickelten Forscher wie Francis Bacon und Robert Boyle erste Ideen zur mechanischen Natur der Wärme. Einen entscheidenden Fortschritt brachte Daniel Bernoulli im Jahr 1738 mit seiner kinetischen Gastheorie. Er stellte fest, dass der Druck eines Gases durch den Impulsübertrag zahlreicher Moleküle auf die Gefäßwände entsteht. Damit legte er den Grundstein für eine mechanische Interpretation der Temperatur als Maß für die durchschnittliche kinetische Energie der Teilchen.
Die kinetische Gastheorie und die Arbeiten von Maxwell und Boltzmann
Trotz Bernoullis Erkenntnisse blieb die kinetische Theorie lange umstritten. Erst im 19. Jahrhundert wurde sie durch die Arbeiten von Rudolf Clausius, James Clerk Maxwell und Ludwig Boltzmann weiterentwickelt.
- Maxwell berechnete 1860 erstmals die Geschwindigkeitsverteilung der Moleküle in einem Gas und führte damit die Verteilungsfunktion ein.
- Boltzmann konnte 1872 mit seinem H-Theorem zeigen, dass sich die Teilchen eines Gases durch zufällige Stöße allmählich einem Gleichgewichtszustand nähern. Dies war eine erste mathematische Formulierung des zweiten Hauptsatzes der Thermodynamik, der die Irreversibilität von Prozessen beschreibt.
- 1884 formulierte Boltzmann seine Theorie zum statistischen Gleichgewicht, die später von Josiah Willard Gibbs weiter ausgebaut wurde.
Kritik und erste Anwendungen in der Quantenmechanik
Obwohl Boltzmanns Ideen die Grundlage der statistischen Mechanik bildeten, wurden sie heftig kritisiert. Ernst Mach und Wilhelm Ostwald gehörten zu den prominenten Gegnern, da die Theorie von der Existenz von Atomen ausging, die damals noch nicht direkt nachweisbar waren.
Doch zu Beginn des 20. Jahrhunderts wurden statistische Methoden auch in anderen physikalischen Bereichen angewandt:
- Max Planck nutzte statistische Konzepte, um seine Strahlungsformel (1900) zu entwickeln, was zur Geburtsstunde der Quantenphysik führte.
- Albert Einstein erklärte 1905 mit Hilfe der Brownschen Bewegung, dass Atome real existieren müssen.
- Gleichzeitig untersuchte Einstein zusammen mit Bose die Quantenstatistik und formulierte die Bose-Einstein-Statistik, die später zur Entdeckung des Bose-Einstein-Kondensats führte.
Was weißt du über die Experimentalphysik?
Moderne Entwicklungen und computergestützte Methoden
In den 1920er Jahren entwickelten Enrico Fermi und Paul Dirac die Fermi-Dirac-Statistik für Fermionen, während Satyendra Nath Bose und Einstein die Bose-Einstein-Statistik für Bosonen beschrieben. Diese Entwicklungen waren entscheidend für das Verständnis von Elektronengasen in Metallen und der Superfluidität.
Albert Einstein Seit die Mathematiker über die Relativitätstheorie hergefallen sind, verstehe ich sie selbst nicht mehr.
Albert Einstein
Mit der Einführung von Computern in der Physik wurden statistische Methoden weiterentwickelt:
- Monte-Carlo-Simulationen ermöglichen es, komplexe Systeme zu analysieren.
- Molekulardynamik-Simulationen helfen, das Verhalten von Flüssigkeiten, Festkörpern und biologischen Systemen vorherzusagen.
Heute ist die statistische Physik ein essenzielles Werkzeug in vielen Wissenschaftsbereichen, von der Materialwissenschaft bis hin zur Kosmologie.
Die Erkenntnisse der technischen Physik gehen auch auf statistische Berechnung zurück.

Womit beschäftigt sich die statistische Physik?
Die statistische Physik ist ein Teilgebiet der Physik, das sich mit der Beschreibung makroskopischer Systeme auf Basis mikroskopischer Gesetzmäßigkeiten beschäftigt. Sie nutzt Methoden der Wahrscheinlichkeitstheorie und der statistischen Mechanik, um das Verhalten von Vielteilchensystemen vorherzusagen. Statt die Bewegung jedes einzelnen Teilchens exakt zu verfolgen, betrachtet sie das System als Ganzes und beschreibt statistische Mittelwerte, die sich aus den Mikrozuständen des Systems ergeben.
❓ Wie entstehen irreversible Prozesse? Die statistische Physik erklärt, warum Entropie in abgeschlossenen Systemen zunimmt, aber noch nicht vollständig, warum sie in manchen Fällen lokal abnehmen kann.
❓ Wie kann man Transportprozesse genau berechnen? Während einige makroskopische Ströme gut verstanden sind, gibt es viele komplexe Systeme (z. B. biologische Prozesse oder Turbulenzen), die schwer vorherzusagen sind.
❓ Wie lässt sich die statistische Physik auf biologische Systeme übertragen? DNA-Faltung, Zellbewegung und Proteininteraktionen sind noch nicht vollständig beschrieben.
Die statistische Physik ist dabei eng mit der mathematischen Physik verknüpft.
Ein einfaches Beispiel: Die Temperatur eines Gases ist nicht die Energie eines einzelnen Moleküls, sondern das statistische Mittel der Bewegungsenergie aller Moleküle im System. Die Temperatur ist also eine makroskopische Größe, die sich aus dem Durchschnitt der mikroskopischen Bewegungsenergien aller Moleküle ergibt.
Die Bedeutung von Ensembles
Um komplexe Systeme zu beschreiben, nutzt die statistische Physik das Konzept der Ensembles. Dabei handelt es sich um eine Sammlung hypothetischer Systeme, die alle möglichen Zustände eines physikalischen Systems repräsentieren. Diese Ensembles ermöglichen die Berechnung von Durchschnittswerten und die Ableitung thermodynamischer Eigenschaften. Die drei wichtigsten sind:
🔹 Mikrokanonisches Ensemble: Wird für isolierte Systeme genutzt, bei denen die Gesamtenergie erhalten bleibt. (z. B. ein abgeschlossener Gasbehälter)
🔹 Kanonisches Ensemble: Beschreibt ein System, das mit seiner Umgebung Wärme austauschen kann, aber nicht seine Teilchenzahl verändert. (z. B. ein Glas Wasser, das Raumtemperatur annimmt)
🔹 Großkanonisches Ensemble: Wird für Systeme genutzt, die sowohl Wärme als auch Teilchen mit der Umgebung austauschen. (z. B. eine chemische Reaktion in einer offenen Umgebung)
Diese Ensembles helfen Physikern, makroskopische Zustandsgrößen wie Temperatur, Druck und Entropie zu berechnen.
Thermodynamik und statistische Physik
Die statistische Physik liefert eine mikroskopische Erklärung für viele thermodynamische Gesetze. Besonders wichtig ist das Boltzmann-Prinzip, das den Zusammenhang zwischen Entropie und der Anzahl möglicher Mikrozustände beschreibt:
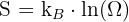
Hierbei ist S die Entropie, kB die Boltzmann-Konstante, und Ω die Anzahl der möglichen Mikrozustände. Dieses Prinzip erklärt, warum sich abgeschlossene Systeme immer einem Zustand maximaler Entropie nähern – also dem thermodynamischen Gleichgewicht.
Verbindung zur Quantenmechanik
Die klassische statistische Physik reicht nicht aus, um das Verhalten von Systemen auf kleinster Skala korrekt zu beschreiben. Deshalb wurde die Quantenstatistik entwickelt, die sich in zwei Hauptklassen unterteilt:
Bose-Einstein-Statistik: Gilt für Bosonen, also Teilchen mit ganzzahligem Spin (z. B. Photonen, Helium-4-Atome). Sie ermöglicht Phänomene wie Supraleitung oder das Bose-Einstein-Kondensat.
Fermi-Dirac-Statistik: Gilt für Fermionen (z. B. Elektronen), die dem Pauli-Prinzip unterliegen. Sie erklärt das Verhalten von Metallen, Halbleitern und den Aufbau von Atomen.
Ohne die statistische Physik wäre unser Verständnis vieler moderner technologischer Entwicklungen, darunter Quantencomputer und Nanotechnologie, nicht möglich.
Kann man statistische Physik studieren?
Da die Statistik in der Physik eine enorm große Rolle spielt, kommt sie in jedem Lehrplan an der Uni im Fach Physik vor. Aber ein eigenes Studium für statistische Physik gibt es nicht.
Stattdessen kannst du dir überlegen, ein verwandte Fach zu studieren. Es gibt einige Optionen: Physik, Mathematik, Medizinische Physik, Technik, Geophysik, Biophysik oder Technische und angewandte Physik.
Naheliegend wäre ein Studium der Physik. Hier gibt es zahlreiche Universitäten, die diesen Studiengang im Bachelor oder Master anbieten: In großen Hochschulstädten wie München findest du außerdem Angebote für physik nachhilfe münchen.
- Uni Saale
- Uni Duisburg-Essen (auch Master of Science)
- Uni Gießen (auch Master of Science)
- RWTH Aachen (auch Master of Science)
- TU Berlin (auch Master of Science)
- Uni Bonn (auch Master of Science)
- Uni Bremen (auch Master of Science)
- Uni Greifswald (auch Master of Science)
- Uni Hamburg (auch Master of Science)
- Uni Heidelberg (auch Master of Science)
- Uni Jena (auch Master of Science)
- KIT Karlsruhe (auch Master of Science)
- Uni Köln (auch Master of Science)
- Uni Konstanz (auch Master of Science)
- Uni Leipzig (auch Master of Science)
Bei Schwierigkeiten kann dir Physik Nachhilfe privat helfen.
Nach dem Studium kann man entweder einen Physik-Master nachschieben oder man wählt einen speziellen Master wie Mathematische Physik oder Technische Physik. In all diesen Studiengängen spielt die Statistik eine große Rolle.
Auch in der Computerphysik spielen statistische Verfahren eine Rolle.
Diese Lehrbücher helfen beim Verständnis
Um die Inhalte der Statistik in der physikalischen Welt zu verstehen, lohnt es sich, einen Blick in die Lehrbücher zu werfen. Wir stellen dir einige vor. Wenn du statt Selbststudium lieber Nachhilfe bevorzugst, findest du in Städten wie Berlin Angebote für physik nachhilfe.

- Statistische Physik: Lehrbuch zur Theoretischen Physik: Dieses Buch von Thorsten Fließbach behandelt die statistischen Grundlagen der Wärmelehre und die konkrete Anwendung statistischer Methoden und Verfahren. Das Buch umfasst eine Einführung in die mathematische Statistik, die Grundlagen der Statistischen Physik sowie der Thermodynamik mit ihren Zustandsgrößen, Statistische Ensembles, Phasenübergänge und viele weitere Themen.
- Theoretische Physik 4 | Thermodynamik und Statistische Physik: Dieses Lehrbuch von Matthias Bartelmann, Björn Feuerbacher, Timm Krüger, Dieter Lüst, Anton Rebhan und Andreas Wipf ermöglicht es interessierten, übersichtliche Erklärungen, Hilfreiche Übungsaufgaben mit Lösungen und Definitionen zu verschiedenen Themen durchzuarbeiten. Der Fokus liegt auf den Themen der statistischen Begründung der Thermodynamik, einfachen thermodynamischen Anwendungen, Ensembles und Zustandssummen sowie der Quantenstatistik.
- Mechanik: Lehrbuch zur Theoretischen Physik I: auch in diesem Lehrbuch von Thorsten Fließbach finden die Leser hilfreiche Erklärungen zur Newtonschen Mechanik mit grundlegenden Konzepten wie Massenpunkt, Bahnkurve oder Bezugssystem.
- Statistische Physik beruhend auf Quantentheorie. Eine Einführung: in diesem Buch von Hermann Schulz wird die Statistische Physik als Anwendungsbereich der Quantentheorie verstanden. Von der relativistischen Feldtheorie bis hin zu Strahlungsfeld-Quantisierung, behandelt dieses Lehrbuch die Grundlagen der Statistik. Dazu bietet es 138 Übungen mit kurzen Lösungen, ausführlichen Rechnungen und guten Erklärungen.
- Statistische Physik. Gleichgewichtstheorie und Kinetik: das Buch von Hartmut Haug eignet sich als Begleitung neben dem Studium und erklärt die Grundlagen der Thermodynamik, sowie zahlreicher weiterer physikalischer Prozesse, bei denen viele Teilchen beteiligt sind.
Die verschiedenen Methoden der Physik sind alle eng miteinander verknüpft und liefern immer wieder Erkenntnisse, die in anderen Bereichen genutzt werden.
Mit KI zusammenfassen:















