Schriftliches Rechnen ist eine fundamentale Fähigkeit in der Mathematik, die Schüler bereits in der Grundschule erlernen und die für Schüler jeder Klasse wichtig ist. Es handelt sich um eine Methode, die es ermöglicht, mathematische Aufgaben schriftlich zu lösen, sei es Addition, Subtraktion, Multiplikation oder Division.
Im Grunde beherrsche ich in Mathe nur diese 4 Grundrehenarten: Addition, Subtraktion, Frustration, Kapitulation
Anonym
Das schriftliche Rechnen ist mehr als nur ein technischer Prozess; es fördert das logische Denken und die Problemlösungsfähigkeiten. Dieser Artikel wird nicht nur die verschiedenen Techniken des schriftlichen Rechnens – Addieren, Subtrahieren, Multiplizieren und Dividieren – detailliert erläutern, sondern auch praktische Tipps und Tricks bereitstellen, die den Umgang mit diesen Rechenarten erleichtern.
Ob es um das Addieren mit Übertrag geht, die Subtraktion mit dem Ergänzungsverfahren, das Multiplizieren großer Ziffern oder das Dividieren mit Rest – mit diesem Artikel lernst du die Methoden, um jede dieser Aufgaben zu bewältigen.

Schriftlich Addieren
Die schriftliche Addition sollte zum Allgemeinwissen in Mathematik dazugehören. Sie ist der Prozess, bei dem zwei oder mehr Zahlen zusammengezählt werden, indem man sie untereinander schreibt und von rechts nach links, also von den Einern zu den höheren Stellen, addiert. Die Summe wird dann unter den Strich an die gleiche Position geschrieben. So kann man einfach und Schritt für Schritt auch große Zahlen miteinander addieren.
Schriftlich Addieren mit Übertrag
Was passiert nun aber, wenn die Zahl, die ich unter den Schrich schreiben muss mehr als eine Stelle hat? Wenn die Summe der Ziffern größer als neun ist, muss ein Übertrag zur nächsten Stelle links hinzugefügt werden. Zum Beispiel, bei der Addition von 467 und 589: Man addiert zuerst die Einer (7+9=16), schreibt die 6 unter die Einer und trägt die 1 zu den Zehnern über, wo dann 6, 8, und die übertragene 1 addiert werden (15), und so weiter.
Schriftliche Addition mit Komma / Dezimalzahl
Bei der Addition von Dezimalzahlen ist es wichtig, die Kommas exakt untereinander zu positionieren. Zum Beispiel: 47,5 + 3,75. Richte die Zahlen so aus, dass die Dezimalstellen übereinstimmen, und addiere wie üblich, wobei du das Komma direkt unter das Komma in der Summe setzt.
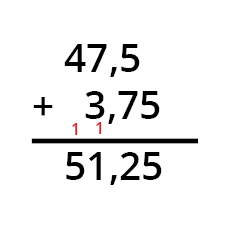
Zum Beispiel: 47,5 + 3,75. Richte die Zahlen so aus, dass die Dezimalstellen übereinstimmen, und addiere wie üblich, wobei du das Komma direkt unter das Komma in der Summe setzt.Rechne also, von rechts nach links 0+5=5, 7+5=12 (also 2 hinschreiben und die 1 übertragen), dann kommt das Komma, 7+3+1=11 (wieder 1 anschreiben und 1 übertragen) und 4+1=5. Das Ergebnis aus 47,5+3,75=51,25.
Mit ein paar Übungen und Textaufgaben wird dir die schriftliche Addition, ob mit Komma, Übertrag oder großen Zahlen schon bald ganz leicht fallen.
Schriftlich Subtrahieren
Die schriftliche Subtraktion ist eine grundlegende mathematische Fähigkeit, die es ermöglicht, eine Ziffer von einer anderen abzuziehen, indem man sie untereinander schreibt und stellengerecht voneinander abzieht. Dies wird in der Grundschule eingeführt und ist essentiell für das Verständnis weiterführender mathematischer Konzepte.
Ähnlich wie bei der Addition gehst du hier von rechts nach links vor nd ziehst die untere Zahl von der jeweils darüberstehenden ab. bei 1785-562 gehst du also so vor: 5-2=3, 8-6=2, 7-5=2, 1-0=1. 1785-562=1223.
Schriftliches Subtrahieren mit Übertrag
Die Subtraktion mit Übertrag tritt auf, wenn die Ziffer der subtrahierenden Zahl (Subtrahend) an einem Punkt größer ist als die entsprechende Ziffer der zu subtrahierenden Zahl (Minuend). Um diese Situation zu lösen, „borgt“ man sich eine Zehner-Einheit von der nächsthöheren Nummer des Minuenden. Diese Zehner-Einheit wird zum Minuenden der niedrigeren Stelle hinzugefügt, und der Minuend der höheren Stelle wird um eins verringert.
Verbessere deine Skills mit Mathe Nachhilfe Frankfurt.
Addition: Summand+Summand=Summe
Subtraktion: Minuend-Subtrahend=Differenz
Multiplikation: Faktor x Faktor=Produkt
Division: Dividend/Divisor=Quotient
Nehmen wir als Beispiel die Subtraktion 705 - 387. Beginnend mit den Einern: 5 ist kleiner als 7. Deshalb borgt man sich eine Zehn von den Zehnern (0), was diese Nummer zu -1 macht. Um diese zu kompensieren, fügt man 10 zu den Einern hinzu, wodurch aus 5 eine 15 wird. Jetzt kann man 7 von 15 abziehen, was 8 ergibt.
Bei den Zehnern hat man nun -1, wodurch man sich eine weitere Zehner-Einheit von den Hundertern (7) borgt. Das vermindert die 7 zu 6, und der Zehner wird zu 9. Subtrahiere nun 8 von 9, was 1 ergibt. Bei den Hundertern subtrahiert man einfach 3 von 6, was 3 ergibt. Das Endergebnis ist 318.
Schriftliche Subtraktion mit Kommazahlen
Beim der Subtraktion von Dezimalzahlen, auch Kommazahlen genannt, ist es genau wie bei der Addition wichtig, die Kommata genau untereinander zu positionieren, um die korrekte Ausrichtung der Dezimalstellen zu gewährleisten.
Wie wäre es mit Mathe Nachhilfe Stuttgart?
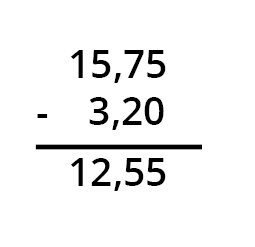
Beispielsweise: 15,75 - 3,2 wird zu 15,75 - 3,20 angeglichen, bevor man die Subtraktion durchführt.
Beginne bei der Subtraktion von rechts nach links, wobei das Komma in der Lösung genau unter den anderen Kommata steht.
Schriftliches Subtrahieren: Abziehverfahren / Ergänzungsverfahren
Beim klassischen Abziehverfahren wird jede Stelle der unteren Ziffer von der entsprechenden Stelle der oberen abgezogen. Wenn eine Zahl kleiner ist als die darunter, ist ein Übertrag notwendig. Beim Ergänzungsverfahren hingegen ermittelt man, welcher Wert zu der unteren Zahl addiert werden muss, um die obere zu erreichen. Dies kann die Aufgabe vereinfachen und ist besonders nützlich bei komplexeren Zahlen.
Schriftlich Dividieren
Das schriftliche Dividieren ist eine wesentliche mathematische Fähigkeit, die es ermöglicht, eine Zahl durch eine andere zu teilen, um ein Ergebnis und gegebenenfalls einen Rest zu ermitteln. Diese Fähigkeit wird auch gerne in Mathe-Tests in Sachaufgaben. Bei der schriftlichen Division geht man in drei Schritten vor.
- Erste Ziffer von links der Linken Zahl (Dividend) durch rechte Zahl (Divisor) teilen.
- Teilergebnis mit Divisor multiplizieren, mit einem Minus-Zeichen unter die linke Zahl schreiben
- Schriftliche Subtraktion

Haben wir zum Beispiel die Aufgabe 853:4, so beginnen wir mit Schritt 1 und rechnen 8:4=2. 2 ist also unser erstes Teilergebnis, welches wir hinter das = schreiben. Nun machen wir weiter mit Schritt 2 und rechnen unser Teilergebnis geteilt durch den Devisor, also 2*4=8. Die 8 schreiben wir nun mit einem Minus unter die erste Zahl von Links unseres Dividenden und dann sind wir schon bei Schritt 3, der Subtraktion. 8-8=0.
Nun nehmen wir uns die nächste Ziffer unseres Dividenen (also die 5) und fangen wieder von vorne an.
Zunächst schreiben wir die 5 neben das Ergebnis unserer Subtraktion von eben, also neben die 0. Dann beginnen wir wieder mit Schritt 1: 5 geteilt durch 4 ist 1, da die 4 nur 1 mal in die 5 passt.
Brauchst Du Mathe Nachhilfe Aachen?
1 ist also unser nächstes Teilerbenis und kommt neben die 2 von eben. 1*4=4 und so schreiben wir die 4 mit einem Minus unter die 5 und machen weiter mit der Subtraktion. 5-4=1 und wir schreiben die 1 unten hin und ziehen die letzte Ziffer unseres Dividenden (3) mit nach unten.
Da wir nun schon bei der letzten Ziffer des Dividenden angekommen sind, müssen wir nun mit allem rechnen, was unter dem Strich steht. Also mit 13. 13:4=3, die 3 ist also unser letztes Teilergebnis. 3*4=12, die 12 schreiben wir mit einem Minus unter die 13 und so bleiben 1 übrig. Das ist unser Rest. Den schreiben wir einfach mit deinem R davor hinter unser Ergebnis. So ergibt die Lösung aus 853:4=213R1.
Schriftliches Dividieren mit Komma / Dezimalzahlen
Beim Dividieren von Dezimalzahlen positioniert man das Komma im Quotienten direkt über dem Komma im Dividenden, sobald der Dividende vollständig aufgeteilt ist. Falls notwendig, kann der Dividend durch Hinzufügen von Nullen erweitert werden, um die Division zu vervollständigen. Beispiel: 12,4 geteilt durch 2 ergibt 6,2.
Schriftliches dividieren mit großen Zahlen
Die Division großer Ziffern folgt demselben Verfahren, erfordert jedoch mehr Schritte und Genauigkeit. Dabei ist es hilfreich, die Zahlen in kleinere, handhabbare Segmente aufzuteilen und den Divisor schrittweise vom größten Stellenwert des Dividenden abzuziehen.
Schriftliche Multiplikation
Schriftliches Multiplizieren ist eine grundlegende Methode in der Mathematik, die es Schülern ermöglicht, große Ziffern miteinander zu multiplizieren, indem sie sie schrittweise miteinander verrechnen. Diese Fähigkeit ist zum Beispiel beim Umrechnen von Maßeinheiten von großer Bedeutung.
Schriftlich multiplizieren
Um schriftlich zu multiplizieren, schreibst du zunächst die Rechnung auf. Die linke Zahl ist der Multiplikator und die rechte der Multiplikand. Du beginnst damit den Multiplikator mit der vorderen Zahl des Multiplikanden zu multiplizieren. Du ziehst einen Strich unter die gesamte Aufgaben und dieses Teilergebnis schreibst du darunter. So machst du weiter mit den anderen Ziffern des Multiplikanden. Schließlich addierst du alle einzelnen Ergebnisse zusammen, um das finale Ergebnis zu erhalten.
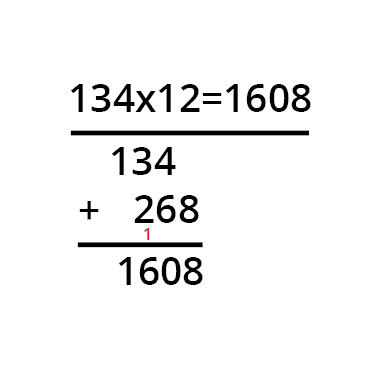
Wenn du nun also 134*12 rechnen möchtest, rechnest du zunächst 1*134. Das ergibt 134. Du ziehst einen Strich unter die Aufgabe und schreibst dieses Teilergebnis so auf, dass die letzte Ziffer (also die 4) genau unter der ersten Ziffer des Multiplikanden steht. Dann machst du weiter und rechnest 134*2=268. Die 268 schreibst du nun um eine Stelle nach rechts versetzt unter das Teilergebnis von eben (134). Dann addierst du schriftlich und kommst auf 1608. 134*12=1608.
Schriftliche Multiplikation mit Komma
Beim Multiplizieren von Dezimalzahlen musst du zunächst so viele Stellen nach rechts verschieben, dass keine Kommas mehr in den Ziffern vorhanden sind. Nachdem du die Multiplikation wie oben beschrieben durchgeführt hast, setzt du das Komma im Ergebnis so, dass die Anzahl der Dezimalstellen der Summe der Dezimalstellen der beiden ursprünglichen Zahlen entspricht. Zum Beispiel: 12,3 multipliziert mit 3,4 ergibt 41,82 da beide Zahlen zusammen zwei Dezimalstellen haben.
Mit KI zusammenfassen:















