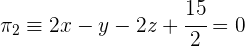Kapitel
Abstand Punkt-Gerade
Der Abstand zwischen einem Punkt 
und einer Geraden 
ist die kürzeste Strecke zwischen Punkt und Gerade.
Dieser Abstand entspricht der Senkrechten, die zwischen dem Punkt und der Geraden gezogen wird.
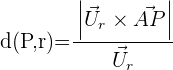
Beispiele
1 Bestimme den Abstand vom Punkt 
zur Geraden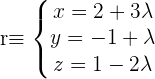 
.
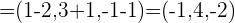
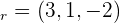
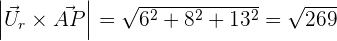
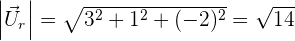
2 Bestimme den Abstand vom Punkt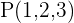 
zur Geraden r
.
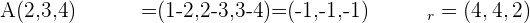
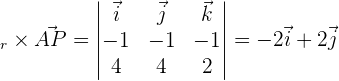
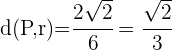
Abstand paralleler Geraden
Der Abstand einer Geraden von einer anderen Parallelen 
ist die Entfernung von einem beliebigen Punkt auf zu .
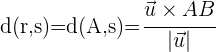
Abstand sich schneidender Geraden
Der Abstand zweier sich schneidender Geraden wird anhand der gemeinsamen Senkrechten gemessen.
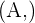und 
sind die linearen Determinanten der Geraden und .
Die Vektoren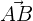 
, 
und 
bestimmen einen Quader, dessen Höhe der Abstand zwischen den zwei Geraden ist.
Das Volumen eines Quaders ist 
.
Wenn man bedenkt, dass das Volumen der Absolutwert des Produkts der drei Vektoren ist und die Fläche der Grundfläche das Vektorprodukt der Richtungsvektoren der Geraden ist, ist die Höhe, d.h. der Abstand zwischen den beiden Punkten:
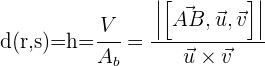
Beispiel:
Bestimme den kürzesten Abstand der Geraden:
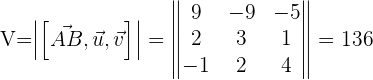
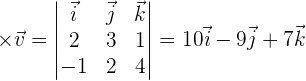
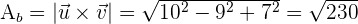
Abstand Punkt-Ebene
Der Abstand zwischen einem Punkt und einer Ebene 
ist die kürzeste Entfernung zwischen dem Punkt und den unendlich vielen Punkten der Ebene.
Diese Entfernung entspricht der Senkrechten, die vom Punkt zur Ebene gezogen wird.
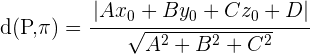
Beispiele
1 Bestimme den Abstand zwischen dem Punkt 
und den Ebenen 
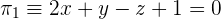und 
.
2 Bestimme den Abstand zwischen dem Punkt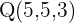 
und der Ebene 
.
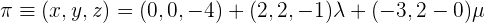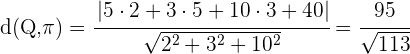
Abstand paralleler Ebenen
Um den Abstand zweier paralleler Ebenen zu berechnen, wird der Abstand zwischen einem beliebigen Punkt auf der einen und der anderen Ebene ermittelt.
Wir können auch wie folgt berechnen:
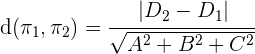
Beispiel
Berechne den Abstand der Ebenen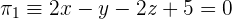 
und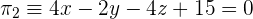 
.
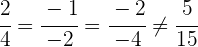
Die beiden Ebenen sind parallel.
Wir wandeln die Gleichung der zweiten Ebene um, sodass die beiden Ebenen denselben Normalenvektor haben.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
