
Brüche mit gleichem Nenner
Die Zähler werden addiert oder subtrahiert, der Nenner bleibt unverändert.
Beispiele:
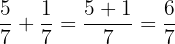

Brüche mit unterschiedlichem Nenner
Um die Addition oder Subtraktion von Brüchen mit unterschiedlichen Nennern zu berechnen, reduzieren wir den Fall auf den oben genannten, d. h. wir erhalten äquivalente Brüche mit demselben Nenner und addieren oder subtrahieren nur die Zähler der erhaltenen Brüche.
Ein möglicher gemeinsamer Nenner ist das kleinste gemeinsame Vielfache der Nenner.
Beispiel:

Das kleinste gemeinsame Vielfache der Nenner  und
und  ist
ist  .
.
Um die entsprechenden Brüche zu erhalten, gehen wir wie folgt vor:
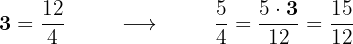

Zum Schluss addieren wir:
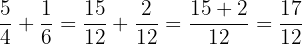
Weiteres Beispiel:
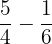
Da die Nenner die gleichen sind wie im vorherigen Beispiel, verwenden wir die bereits bekannten Informationen.
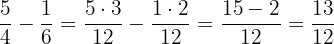
Regeln für die Addition
1 Intern
Das Ergebnis der Addition zweier rationaler Zahlen ist eine weitere rationale Zahl.
Wenn 
Beispiel:

Die Addition zweier rationaler Zahlen  und
und  ergibt
ergibt  , was auch eine rationale Zahl ist.
, was auch eine rationale Zahl ist.
2 Assoziativ
Die Art und Weise, wie die Summanden angeordnet werden, hat keinen Einfluss auf das Ergebnis.

Beispiel:

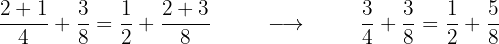
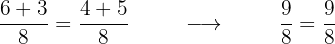
3 Kommutativ
Die Reihenfolge der Summanden ändert nichts an der Summe.

Beispiel:
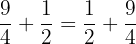
4 Neutrales Element
Die 0 ist das neutrale Element der Addition, da jede Zahl, die mit ihr addiert wird, dieselbe Zahl ergibt.
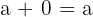
Beispiel:

5 Gegenelement
Zwei Zahlen sind entgegengesetzt, wenn ihre Summe null ergibt.
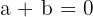
Das Gegenteil einer Zahl  in der Summe wird mit
in der Summe wird mit  angegeben.
angegeben.
Beispiel:

Das Gegenteil des Gegenteils einer Zahl ist gleich dieser Zahl.

Beispiel:
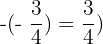
Aufgrund dieser Eigenschaften wird die Differenz zweier rationaler Zahlen als die Summe aus dem Minuenden und dem Gegenteil des Subtrahenden definiert.
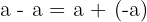
Beispiel:
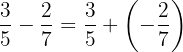
Mit KI zusammenfassen:












