Echte Brüche
Echte Brüche sind Brüche, deren Zähler kleiner als der Nenner ist. Ihr Wert liegt zwischen 0 und 1.
Beispiel:
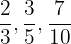
Unechte Brüche
Unechte Brüche sind Brüche, deren Zähler größer als der Nenner ist. Ihr Wert ist größer als 1.
Beispiel:
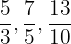
Gemischte Zahl
Eine gemischte Zahl oder ein gemischter Bruch besteht aus einem ganzen Teil und einem Bruchteil.
Eine gemischte Zahl in einen unechten Bruch umwandeln:
1 Der Nenner bleibt gleich
2 Der Zähler ergibt sich aus der Summe des Produkts der ganzen Zahl mit dem Nenner und dem Zähler der gemischten Zahl.
Beispiel:
Einen unechten Bruch in eine gemischte Zahl umwandeln:
1 Der Zähler wird durch den Nenner dividiert.
2 Der Quotient ist der ganzzahlige Teil der gemischten Zahl.
3 Der Rest ist der Zähler des Bruchs.
4 Der Nenner ist der gleiche wie der des unechten Bruchs.
Beispiel:
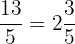
Dezimalbrüche
Dezimalbrüche haben als Nenner eine Potenz von 10.
Beispiel:
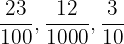
Gleichwertige Brüche
Zwei Brüche sind gleichwertig, wenn gilt:
Beispiel:
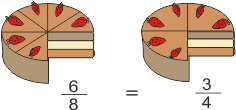
Berechne, ob die Brüche 
und 
gleichwertig sind.
, somit sind sie gleichwertig.
Wenn man den Zähler und Nenner eines Bruchs mit einer ganzen Zahl ungleich 0 multipliziert oder dividiert, erhält man einen anderen Bruch, der dem gegebenen Bruch entspricht.
Dieses Vorgehnen nennt man "erweitern".
Beispiel:
Brüche vereinfachen
Einen Bruch zu vereinfachen bedeutet, ihn in einen einfacheren gleichwertigen Bruch umzuwandeln.
1 Um einen Bruch zu vereinfachen, dividieren wir Zähler und Nenner durch dieselbe Zahl.
2 Wir beginnen mit der Vereinfachung, indem wir die ersten Primzahlen ausprobieren: 2, 3, 5, 7, ... Das heißt, wir versuchen, Zähler und Nenner durch 2 zu teilen, solange dies möglich ist, dann gehen wir zu 3 über und so weiter.
3 Der Vorgang wird wiederholt, bis keine gemeinsamen Teiler mehr vorhanden sind.
4 Wenn die Terme des Bruchs auf Nullen enden, beginnen wir damit, die gemeinsamen Nullen am Ende des Zählers und Nenners zu entfernen, was einer Division von Zähler und Nenner durch dieselbe Potenz von 10 entspricht.
5 Wenn die Zahl, durch die wir dividieren, der größte gemeinsame Teiler von Zähler und Nenner ist, erhalten wir einen nicht kürzbaren Bruch, der dem ursprünglichen Bruch entspricht.
Beispiel:
Nicht kürzbare Brüche
Nicht kürzbare Brüche sind Brüche, die nicht vereinfacht werden können. Dies ist der Fall, wenn Zähler und Nenner teilerfremd sind, d. h. wenn der größte gemeinsame Teiler beider Zahlen 1 ist.
Beispiel:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
