Kapitel

Dezimalzahlen in Brüche umwandeln
Um Dezimalzahlen in Brüche umzurechnen, müssen wir 3 wichtige Dinge beachten:
- Wenn die Dezimalzahl nicht periodisch ist, dividieren wir durch
1, 10, 100, ..., je nachdem - Wenn die Dezimalzahlen periodisch sind, dividieren wir durch
9,99,999,.., je nachdem - Bei Dezimalzahlen, bei denen nur ein Teil periodisch ist, stehen 9,90,900,… im Nenner, je nachdem
Als Beispiel nehmen wir die folgenden 3 Zahlen
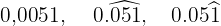
Der erste Fall ist recht einfach, es handelt sich um eine Zahl mit 4 Dezimalzahlen, von denen keine periodisch ist. Um sie in einen Bruch umzuwandeln, genügt es, 51 als Zähler zu schreiben und in den Nenner eine 1 mit vier Nullen zu setzen, da es 4 Dezimalstellen gibt. Also haben wir:
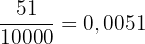
Im zweiten Fall haben wir eine Zahl mit 3 Dezimalstellen und die 3 Ziffern sind periodisch. Dann nehmen wir als Zähler die Zahl 51 und als Nenner setzen wir drei Neunen, da sie 3 periodische Ziffern sind. Somit haben wir:

Im dritten Fall haben wir eine Zahl mit drei Dezimalstellen, aber nur eine ist periodisch. Also nehmen wir als Zähler die Zahl 51 und ziehen 5 Einheiten ab, da die Zahl 5, die in den Dezimalstellen steht, nicht periodisch ist, und als Nenner setzen wir die Zahl 9 mit zwei Nullen.
Denke daran, dass wir die 9 besetzen, weil es eine periodische Zahl gibt und wir fügen zwei Nullen hinzu, weil es 2 nichtperiodische Dezimalstellen gibt. Somit haben wir:

Im Anschluss vereinfachen wir, wenn möglich, die Brüche
Wandle die folgenden Dezimalzahlen in Brüche um
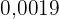
Es handelt sich um eine Zahl mit 4 Dezimalstellen, von denen keine periodisch ist. Um sie in einen Bruch umzuwandeln, genügt es, 19 als Zähler zu schreiben und in den Nenner eine 1 mit vier Nullen zu setzen, da es 4 Dezimalstellen gibt. Wir erhalten:
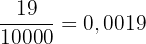
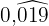
Im Zähler schreiben wir die Zahl ohne Komma und im Nenner 3 Neunen, weil es 3 periodische Ziffern gibt.
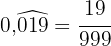
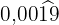
Im Zähler schreiben wir die Zahl ohne Komma und im Nenner stehen zwei Neunen und zwei Nullen, weil wir eine periodische Ziffer haben und es zwei Dezimalstellen gibt
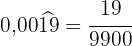
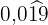
Im Zähler schreiben wir die Zahl ohne Komma und im Nenner stehen zwei Neunen und eine Null, weil wir zwei periodische Ziffern haben und es eine Dezimalstelle gibt
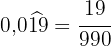
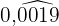
Im Zähler schreiben wir die Zahl ohne Komma und im Nenner stehen vier Neunen
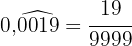
Führe die folgenden Rechenoperationen mit Potenzen durch
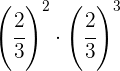
Um Potenzen mit derselben Basis zu multiplizieren, werden die Exponenten addiert
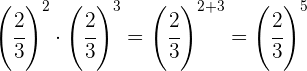
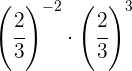
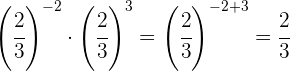
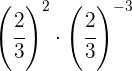
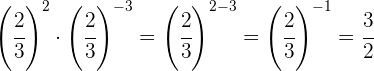
Um das negative Vorzeichen aus dem Exponenten zu entfernen, müssen wir den Kehrwert schreiben
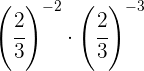
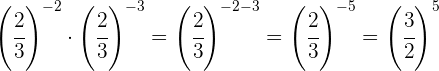
Wir entfernen das negative Vorzeichen aus dem Exponenten und nehmen den Kehrwert
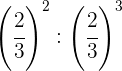
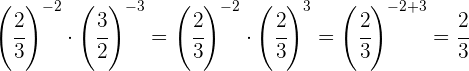
Da sie nicht die gleiche Basis haben, nehmen wir den Kehrwert der zweiten Potenz, da sein Exponent negativ ist
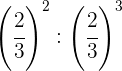
Um Potenzen mit der gleichen Basis zu dividieren, subtrahieren wir die Exponenten
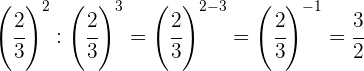
Wir nehmen den Kehrwert, d.h. wir ändern das Vorzeichen des Exponenten
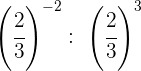
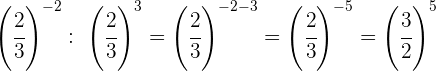
Wir ändern das Vorzeichen des Exponenten, indem wir den Kehrwert nehmen
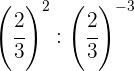
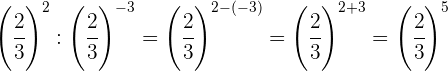
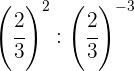
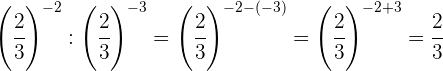
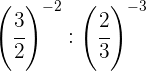
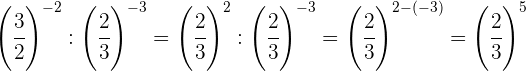
Wir nehmen den Kehrwert der ersten Potenz, um das Vorzeichen des Exponenten zu ändern
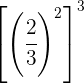
Um Potenzen mit der gleichen Basis zu multiplizieren, multipliziert man die Exponenten
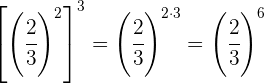
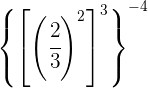
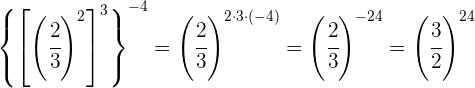
Wir nehmen den Kehrwert, um das Vorzeichen des Exponenten zu ändern
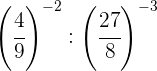
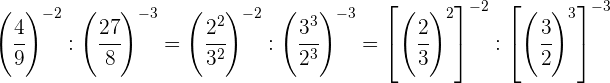
Wir zerlegen die Zahlen in Faktoren, innerhalb jeder Klammer dividieren wir Potenzen mit demselben Exponenten, also dividieren wir die Basen und lassen denselben Exponenten
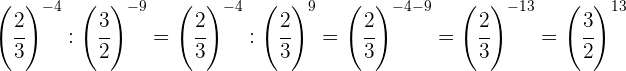
Wir nehmen den Kehrwert der ersten Potenz, um das Vorzeichen des Exponenten zu ändern, und machen dasselbe mit dem Ergebnis
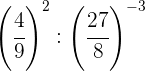
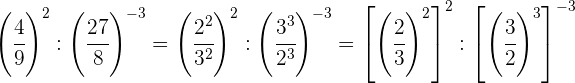
Wir zerlegen die Zahlen in Faktoren, innerhalb jeder Klammer dividieren wir Potenzen mit demselben Exponenten, also dividieren wir die Basen und lassen denselben Exponenten
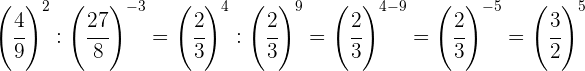
Wir nehmen den Kehrwert der ersten Potenz, um das Vorzeichen des Exponenten zu ändern, und machen dasselbe mit dem Ergebnis
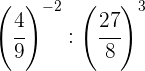
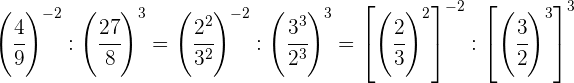
Wir zerlegen die Zahlen in Faktoren, innerhalb jeder Klammer dividieren wir Potenzen mit demselben Exponenten, also dividieren wir die Basen und lassen denselben Exponenten
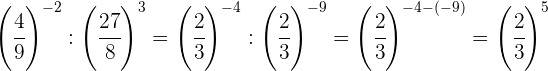
Wir nehmen den Kehrwert der ersten Potenz, um das Vorzeichen des Exponenten zu ändern, und machen dasselbe mit dem Ergebnis
Führe folgende Berechnungen durch
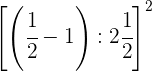
Wir wanden den Bruch in eine gemischte Zahl um 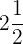 .
.
Wir lassen den Nenner (2) gleich und der Zähler ist die Summe aus der Multiplikation der ganzen Zahl (2) mit dem Nenner (2) plus dem Zähler der gemischten Zahl (1).
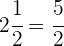
Wir bringen die Brüche auf ihren gemeinsamen Nenner.
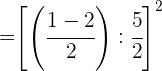
Wir führen die Operationen mit den Zählern durch
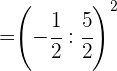
Wir dividieren
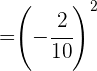
Wir vereinfachen und rechnen mit der Potenz
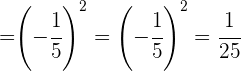
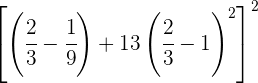
Wir bringen die Brüche auf ihren gemeinsamen Nenner.
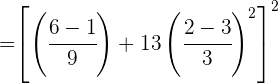
Wir führen die Rechenoperationen im Zähler durch
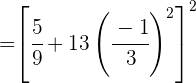
Wir berechnen die Potenz
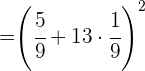
Wir multiplizieren
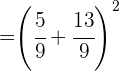
Wir addieren und berechnen die Potenz
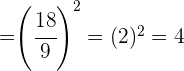
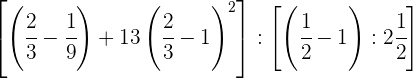
Wir wandeln den Bruch in eine gemischte Zahl um 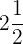 .
.
Wir lassen den Nenner (2) gleich und der Zähler ist die Summe aus der Multiplikation der ganzen Zahl (2) mit dem Nenner (2) plus dem Zähler der gemischten Zahl (1).
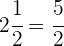
Wir bringen die Brüche in jeder Klammer auf ihren gemeinsamen Nenner.
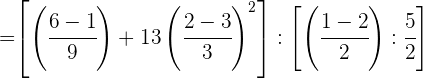
Wir führen die Rechenoperationen in den Zählern durch
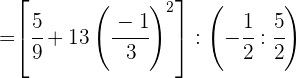
Wir berechnen die Potenz
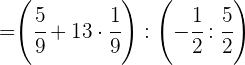
Wir multiplizieren in der ersten Klammer und dividieren in der zweiten Klammer
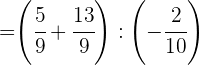
Wir addieren in der ersten Klammer und vereinfachen in der zweiten Klammer
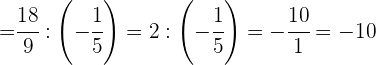
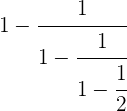
Zunächst führen wir den letzten Teil des Nenners aus
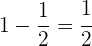
Wir gehen wie folgt vor
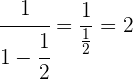
Wir subtrahieren
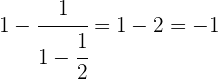
Und somit
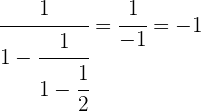
Wir subtrahieren
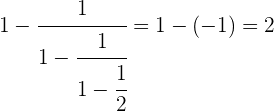
Wenn man die Schritte nacheinander durchführt, erhält man
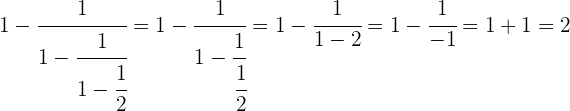
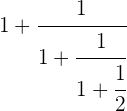
Zunächst führen wir den letzten Teil des Nenners aus
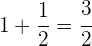
Wir machen es umgekehrt
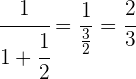
Wir addieren
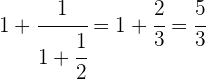
Wir machen es umgekehrt
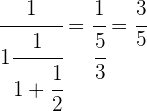
Wir addieren
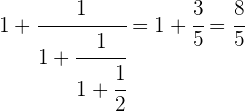
Wenn man die Schritte nacheinander durchführt, erhält man
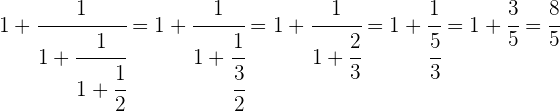
Berechne, welcher Bruchteil einer Einheit entspricht
Die Hälfte der Hälfte
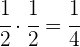
Die Hälfte eines Drittels
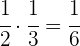
Ein Drittel der Hälfte
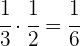
Die Hälfte eines Viertels
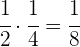
Die Hälfte von einem Viertel von einem Drittel
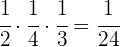
Anwendungen
Elena geht mit 180 € einkaufen. Sie gibt 3/5 dieses Betrags aus. Wie viel hat sie noch übrig?
Um 3/5 von 180 zu ermitteln, müssen wir mit 3 multiplizieren und durch 5 dividieren.
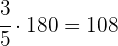 €
€
Ihr bleibt der ursprüngliche Betrag (180) abzüglich der ausgegebenen 3/5 (108).
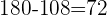 €
€
Zwei Autos A und B fahren die gleiche Strecke von 572 km. Auto A hat 5/11 der Strecke zurückgelegt, während Auto B 6/13 der Strecke zurückgelegt hat. Welches Auto ist zuerst da? Wie viele Kilometer hat jedes Auto zurückgelegt?
Wir vergleichen die Strecken von A und B. Dazu bringen wir die Brüche auf einen gemeinsamen Nenner, derjenige mit dem größten Zähler ist der mit der längsten Strecke
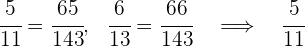
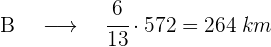
Vor ein paar Jahren war Peter 24 Jahre alt, also 2/3 seines heutigen Alters. Wie alt ist Peter?
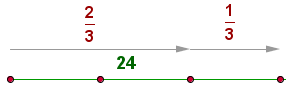
24 entspricht zwei Teilen des Alters. Also berechnen wir, wie viel ein Teil wert ist (24:2), und das Ergebnis wird mit der Gesamtzahl der Teile (3) multipliziert.
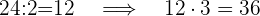 Jahre
Jahre
Bei den Kommunalwahlen in einem Dorf entfielen 3/11 der Stimmen auf Partei A, 3/10 auf Partei B, 5/14 auf Partei C und der Rest auf Partei D. Die Gesamtzahl der Stimmen betrug 15.400. Berechne:
1 Die Anzahl der von jeder Partei erhaltenen Stimmen.
2 Die Zahl der Stimmenthaltungen entspricht 5/8 des Wählerverzeichnisses.
Wir berechnen die Stimmen für jede der Parteien
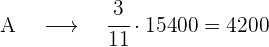 Stimmen
Stimmen
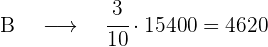 Stimmen
Stimmen
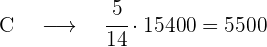 Stimmen
Stimmen
D erhält die Gesamtstimmen abzüglich der von den anderen Parteien erhaltenen Stimmen
Die Gesamtzahl der Wähler:innen ist 8/8, d.h. 1.
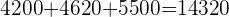
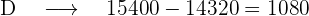
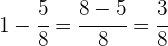
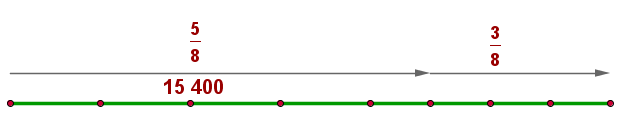
Die Gerade ist in 8 gleiche Teile unterteilt. Um den Betrag zu ermitteln, den jeder Teil darstellt, müssen wir berücksichtigen, dass die ersten 5 Teile (die Stimmen) 15 400 ergeben, also ist ein Teil 15 400 geteilt durch 5, was 3080 ergibt. Die anderen drei Teile (die Stimmenthaltungen) erhält man, indem man 3 mit 3080 multipliziert.
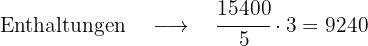
Ein Vater teilt 1800 € unter seinen Kindern auf. Er gibt 4/9 dieses Betrags an das älteste, 1/3 an das mittlere und den Rest an das jüngste Kind. Welchen Betrag hat jedes von ihnen erhalten, und welchen Bruchteil des Geldes hat das dritte Kind erhalten?
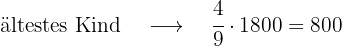
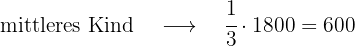
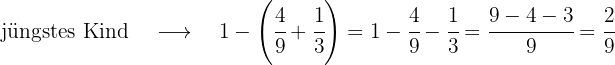
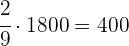
Mit KI zusammenfassen:












