Ein Scheinwerfer leuchtet alle  Sekunden, ein anderer alle 18 Sekunen und ein dritter Scheinwerfer leuchtet jede Minute. Um
Sekunden, ein anderer alle 18 Sekunen und ein dritter Scheinwerfer leuchtet jede Minute. Um  Uhr leuchten alle drei Scheinwerfer gleichzeitig. Ermittle, wie oft sie in den nächsten fünf Minuten gleichzeitig leuchten werden.
Uhr leuchten alle drei Scheinwerfer gleichzeitig. Ermittle, wie oft sie in den nächsten fünf Minuten gleichzeitig leuchten werden.
Ein Scheinwerfer leuchtet alle  Sekunden, ein anderer alle 18 Sekunen und ein dritter Scheinwerfer leuchtet jede Minute. Um
Sekunden, ein anderer alle 18 Sekunen und ein dritter Scheinwerfer leuchtet jede Minute. Um  Uhr leuchten alle drei Scheinwerfer gleichzeitig. Ermittle, wie oft sie in den nächsten fünf Minuten gleichzeitig leuchten werden.Wir müssen alle Zeitangaben in der gleichen Einheit angeben, zum Beispiel in Sekunden.
Uhr leuchten alle drei Scheinwerfer gleichzeitig. Ermittle, wie oft sie in den nächsten fünf Minuten gleichzeitig leuchten werden.Wir müssen alle Zeitangaben in der gleichen Einheit angeben, zum Beispiel in Sekunden.
Der erste Scheinwerfer leuchtet in Sekunde  , in Sekunde
, in Sekunde  , in Sekunde
, in Sekunde  , in Sekunde
, in Sekunde  , in Sekunde
, in Sekunde  ... Dies sind jeweils Vielfache von
... Dies sind jeweils Vielfache von 
Der zweite Scheinwerfer leuchtet in Sekunde  , in Sekunde
, in Sekunde  , in Sekunde
, in Sekunde  , in Sekunde
, in Sekunde  , in Sekunde
, in Sekunde  ... Dies sind jeweils Vielfache von
... Dies sind jeweils Vielfache von 
Der dritte Scheinwerfer leuchtet in Sekunde  , in Sekunde
, in Sekunde  , in Sekunde
, in Sekunde 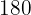 , in Sekunde
, in Sekunde  , in Sekunde
, in Sekunde  ... Dies sind jeweils Vielfache von
... Dies sind jeweils Vielfache von 
Die Sekunde, in der alle drei Scheinwerfer leuchten, ist die kleinste Zahl, die sich durch  und
und  teilen lässt.
teilen lässt.
Deshalb müssen wir das  berechnen
berechnen
Zunächst zerlegen wir die Zahlen in Primfaktoren






Wir nehmen die Faktoren, die in mindestens einer der Zerlegungen vorkommen und den jeweils größeren der Ausgangsexponenten

Sie treffen das erste Mal nach 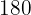 Sekunden zusammen
Sekunden zusammen
 , sie treffen alle
, sie treffen alle  Minuten zusammen, weshalb sie innerhalb von
Minuten zusammen, weshalb sie innerhalb von  Minuten nur einmal zusammentreffen.
Minuten nur einmal zusammentreffen.
Die drei Scheinwerfer leuchten gleichzeitig um 18:33 Uhr.
Ein Mann reist alle  Tage nach Barcelona und ein anderer alle
Tage nach Barcelona und ein anderer alle  Tage. Heute sind beide in Barcelona. In wie vielen Tagen werden sie wieder beide gleichzeitig in Barcelona sein?
Tage. Heute sind beide in Barcelona. In wie vielen Tagen werden sie wieder beide gleichzeitig in Barcelona sein?
Ein Mann reist alle  Tage nach Barcelona und ein anderer alle
Tage nach Barcelona und ein anderer alle  Tage. Heute sind beide in Barcelona. In wie vielen Tagen werden sie wieder beide gleichzeitig in Barcelona sein?Der erste Mann reist an Tag
Tage. Heute sind beide in Barcelona. In wie vielen Tagen werden sie wieder beide gleichzeitig in Barcelona sein?Der erste Mann reist an Tag  , Tag
, Tag  , Tag
, Tag  , Tag
, Tag  , Tag
, Tag  ... Dies sind jeweils Vielfache von
... Dies sind jeweils Vielfache von 
Der zweite Mann reist an Tag  , Tag
, Tag  , Tag
, Tag  , Tag
, Tag  , Tag
, Tag  ... Dies sind jeweils Vielfache von
... Dies sind jeweils Vielfache von 
Die beiden treffen zusammen, wenn sie am selben Tag reisen, d. h. wenn sie an einem Tag reisen, der ein Vielfaches von  und
und  ist. Der erste Tag, an dem sie zusammentreffen, ist die kleinste Zahl, die durch
ist. Der erste Tag, an dem sie zusammentreffen, ist die kleinste Zahl, die durch  und
und  geteilt werden kann.
geteilt werden kann.
Deshalb müssen wir das  berechnen
berechnen
Zunächst zerlegen wir die Zahlen in Primfaktoren




Wir nehmen die Faktoren, die in mindestens einer der Zerlegungen vorkommen und den jeweils größeren der Ausgangsexponenten

Innerhalb von 72 Tagen
Wie lautet die kleinste Zahl, die bei getrennter Division durch  und
und  jeweils
jeweils  als Rest ergibt?
als Rest ergibt?
Wie lautet die kleinste Zahl, die bei getrennter Division durch  und
und  jeweils
jeweils  als Rest ergibt?Die kleinste Zahl, die durch
als Rest ergibt?Die kleinste Zahl, die durch  und
und  dividiert werden kann, ist das kgV, zu dem wir
dividiert werden kann, ist das kgV, zu dem wir  addieren, sodass die Division des kgV durch eine der vier Zahlen einen Rest von
addieren, sodass die Division des kgV durch eine der vier Zahlen einen Rest von  ergibt
ergibt
Zunächst zerlegen wir die Zahlen in Primfaktoren








Wir nehmen die Faktoren, die in mindestens einer der Zerlegungen vorkommen und den jeweils größeren der Ausgangsexponenten

 729
729
In einem Weinkeller lagern  Weinfässer mit folgenden Fasssungsvermögen:
Weinfässer mit folgenden Fasssungsvermögen: 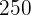 l,
l,  l und
l und 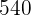 l. Der Inhalt soll in eine bestimmte Anzahl von gleich großen Karaffen abgefüllt werden. Berechne das maximale Fassungsvermögen dieser Karaffen, so dass der in jedem der Fässer enthaltene Wein in sie gefüllt werden kann sowie die Anzahl der benötigten Karaffen.
l. Der Inhalt soll in eine bestimmte Anzahl von gleich großen Karaffen abgefüllt werden. Berechne das maximale Fassungsvermögen dieser Karaffen, so dass der in jedem der Fässer enthaltene Wein in sie gefüllt werden kann sowie die Anzahl der benötigten Karaffen.
In einem Weinkeller lagern  Weinfässer mit folgenden Fasssungsvermögen:
Weinfässer mit folgenden Fasssungsvermögen: 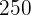 l,
l,  l und
l und 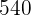 l. Der Inhalt soll in eine bestimmte Anzahl von gleich großen Karaffen abgefüllt werden. Berechne das maximale Fassungsvermögen dieser Karaffen, so dass der in jedem der Fässer enthaltene Wein in sie gefüllt werden kann sowie die Anzahl der benötigten Karaffen.Um die
l. Der Inhalt soll in eine bestimmte Anzahl von gleich großen Karaffen abgefüllt werden. Berechne das maximale Fassungsvermögen dieser Karaffen, so dass der in jedem der Fässer enthaltene Wein in sie gefüllt werden kann sowie die Anzahl der benötigten Karaffen.Um die 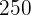 l in Karaffen zu füllen, müssen wir eine Zahl wählen, die ein Teiler von
l in Karaffen zu füllen, müssen wir eine Zahl wählen, die ein Teiler von 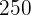 ist
ist
Um die  l in Karaffen zu füllen, müssen wir eine Zahl wählen, die ein Teiler von
l in Karaffen zu füllen, müssen wir eine Zahl wählen, die ein Teiler von  ist
ist
Um die 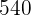 l in Karaffen zu füllen, müssen wir eine Zahl wählen, die ein Teiler von
l in Karaffen zu füllen, müssen wir eine Zahl wählen, die ein Teiler von 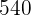 ist
ist
Da der Inhalt der Karaffen so groß wie möglich sein muss, müssen wir den  berechnen
berechnen
Zunächst zerlegen wir die Zahlen in Primfaktoren






Wir nehmen die gemeinsamen Faktoren mit dem niedrigsten Exponenten

Fassungsvermögen der Karaffen  l
l
Anzahl der Karaffen für 
Anzahl der Karaffen für 
Anzahl der Karaffen für 
Anzahl der Karaffen:  115 Karaffen.
115 Karaffen.
Der Boden eines Raumes soll gefliest werden. Der Raum ist  m lang und
m lang und  m breit.
m breit.
Berechne die Seite der Fliese und die Anzahl der Fliesen so, dass die Anzahl der zu verlegenden Fliesen so gering wie möglich gehalten wird und keine Fliesen geschnitten werden müssen.
Der Boden eines Raumes soll gefliest werden. Der Raum ist  m lang und
m lang und  m breit. Berechne die Seite der Fliese und die Anzahl der Fliesen so, dass die Anzahl der zu verlegenden Fliesen so gering wie möglich gehalten wird und keine Fliesen geschnitten werden müssen.Um die Anzahl der Fliesen so gering wie möglich zu halten, müssen die Fliesen eine möglichst große Fläche haben
m breit. Berechne die Seite der Fliese und die Anzahl der Fliesen so, dass die Anzahl der zu verlegenden Fliesen so gering wie möglich gehalten wird und keine Fliesen geschnitten werden müssen.Um die Anzahl der Fliesen so gering wie möglich zu halten, müssen die Fliesen eine möglichst große Fläche haben
Wir müssen deshalb den größten gemeinsamen Teiler bestimmen
Da Fliesen normalerweise in Zentimetern gemessen werden, rechnen wir alles in Zentimeter um.



Wir zerlegen die Zahlen in Primfaktoren




Wir nehmen die gemeinsamen Faktoren mit dem niedrigsten Exponenten
 Seitenlänge
Seitenlänge
Wir berechnen die Fläche einer Fliese

Wir berechnen die Anzahl der Fliesen, indem wir die Gesamtfläche durch die Fläche einer Fliese teilen.
 15 Fliesen
15 Fliesen
Ein Händler möchte  Äpfel und
Äpfel und  Orangen in Kisten packen. Und zwar so, dass jede Kiste dieselbe Anzahl an Äpfel oder Orangen enthält und so viele Früchte wie möglich sich darin befinden. Bestimme die Anzahl der Orangen in jeder Kiste und die Anzahl der benötigten Kisten.
Orangen in Kisten packen. Und zwar so, dass jede Kiste dieselbe Anzahl an Äpfel oder Orangen enthält und so viele Früchte wie möglich sich darin befinden. Bestimme die Anzahl der Orangen in jeder Kiste und die Anzahl der benötigten Kisten.
Ein Händler möchte  Äpfel und
Äpfel und  Orangen in Kisten packen. Und zwar so, dass jede Kiste dieselbe Anzahl an Äpfel oder Orangen enthält und so viele Früchte wie möglich sich darin befinden. Bestimme die Anzahl der Orangen in jeder Kiste und die Anzahl der benötigten Kisten.Um
Orangen in Kisten packen. Und zwar so, dass jede Kiste dieselbe Anzahl an Äpfel oder Orangen enthält und so viele Früchte wie möglich sich darin befinden. Bestimme die Anzahl der Orangen in jeder Kiste und die Anzahl der benötigten Kisten.Um  Äpfel in kleinere Kisten mit der gleichen Anzahl von Äpfeln zu packen, muss man eine Zahl wählen, die ein Teiler von
Äpfel in kleinere Kisten mit der gleichen Anzahl von Äpfeln zu packen, muss man eine Zahl wählen, die ein Teiler von  ist.
ist.
Für die Orangen benötigen wir einen Teiler von 
Da jede Kiste die größtmögliche Stückzahl enthalten muss, müssen wir den  ermitteln
ermitteln
Wir zerlegen die Zahlen in Primfaktoren




Wir nehmen die gemeinsamen Faktoren mit dem niedrigsten Exponenten

 Stück in jeder Kiste
Stück in jeder Kiste
Kisten mit Orangen 
Kisten mit Äpfeln 
Benötigte Kisten  200
200
Wie groß ist die größte quadratische Fliese, die genau eine Anzahl von Malen in einen Raum mit einer Länge von  m und einer Breite von
m und einer Breite von  m passt? Und wie viele Fliesen werden benötigt?
m passt? Und wie viele Fliesen werden benötigt?
Wie groß ist die größte quadratische Fliese, die genau eine Anzahl von Malen in einen Raum mit einer Länge von  m und einer Breite von
m und einer Breite von  m passt? Und wie viele Fliesen werden benötigt?Um die Anzahl der Fliesen so gering wie möglich zu halten, müssen die Fliesen eine möglichst große Oberfläche haben
m passt? Und wie viele Fliesen werden benötigt?Um die Anzahl der Fliesen so gering wie möglich zu halten, müssen die Fliesen eine möglichst große Oberfläche haben
Daher müssen wir den größten gemeinsamen Teiler finden
Da Fliesen normalerweise in Zentimetern gemessen werden, rechnen wir alles in Zentimeter um.


Fläche 
Wir zerlegen die Zahlen in Primfaktoren




 Seitenlänge
Seitenlänge
Wir berechnen die Fläche einer Fliese

Wir berechnen die Anzahl der Fliesen, indem wir die Gesamtfläche durch die Fläche einer Fliese teilen
 20 Fliesen
20 Fliesen
Mit KI zusammenfassen:



