Aufgaben mit Quadratwurzeln

Berechne die Quadratwurzel aus: 264

Lösung:

Wir teilen die Zahlen in Zweiergruppen auf, beginnend von rechts

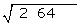
Mit der ersten Ziffer (2) berechnen wir die Zahl, die dem Quadrat der Ziffer am nächsten kommt; sie darf nicht größer sein als die Ziffer

1² < 2 < 2², also nehmen wir 1

Diese Zahl (1) schreiben wir in das Kästchen. Sie ist die 1. Ziffer der Wurzel

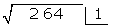
Das Quadrat der erhaltenen Zahl (1²) wird von der ersten Ziffer subtrahiert

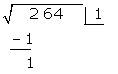
Hinter den Rest schreiben wir die nächste Zifferngruppe des Radikanden (64). Wir trennen die erste Ziffer rechts (4) von der gebildeten Zahl ab und teilen den Rest (16) durch das Doppelte der Zahl im Kästchen, also durch 2 · 1=2

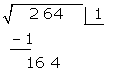
16 : 2 = 8

Unter das Kästchen setzen wir ein weiteres Kästchen mit dem erhaltenen Doppelten (2), gefolgt vom Quotienten der Division (8), und die gebildete Zahl wird mit dem erhaltenen Quotienten (8) multipliziert

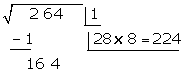
Da diese Zahl größer ist als der Rest (164), müssen wir mit kleineren Zahlen probieren, bis das Produkt kleiner ist als der Rest

27 · 7 = 189

26 · 6 = 156

Bei 6 ist das Ergebnis kleiner als der Rest, also schreiben wir 6 als zweite Ziffer der Wurzel

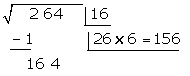
Wir subtrahieren das erhaltene Produkt (156) vom Rest (164)

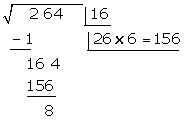
Das bedeutet, dass 16 die Wurzel und 8 der Rest ist.

Das Verfahren liefert ganzzahlige Lösungen, d. h. es findet das Quadrat, das am nächsten links von der Zahl 264 liegt, also 16², und ermittelt den Betrag, der benötigt wird, um die betreffende Zahl 8 zu erreichen.

Es ist möglich, Dezimalwerte zu ermitteln, falls erforderlich.

Wir überprüfen das Ergebnis, indem wir den Test durchführen:

16² + 8 = 256 + 8 = 264

Berechne die Wurzel aus: 6256Lösung:
Wir teilen die Zahlen in Zweiergruppen auf, beginnend von rechts

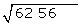
Mit der ersten Ziffer (64) berechnen wir die Zahl, die dem Quadrat der Ziffer am nächsten kommt; sie darf nicht größer sein als die Ziffer

7² < 62 < 8², also nehmen wir 7

Diese Zahl (7) schreiben wir in das Kästchen. Sie ist die 1. Ziffer der Wurzel

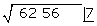
Das Quadrat der erhaltenen Zahl (7²) wird von der ersten Ziffer subtrahiert

Hinter den Rest schreiben wir die nächste Zifferngruppe des Radikanden (56). Wir trennen die erste Ziffer rechts (6) von der gebildeten Zahl ab und teilen den Rest (135) durch das Doppelte der Zahl im Kästchen, also durch 2 · 7=14

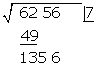
135 : 14 = 9,6     Wir probieren mit 9

Unter das Kästchen setzen wir ein weiteres Kästchen mit dem erhaltenen Doppelten (14), gefolgt vom Quotienten der Division (9), und die gebildete Zahl wird mit dem erhaltenen Quotienten (9) multipliziert

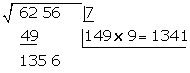
Wir subtrahieren das erhaltene Produkt (1341) vom Rest (1356). Der Rest ist 15

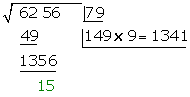
Das bedeutet, dass 79 die Wurzel und 15 der Rest ist.

Wir überprüfen das Ergebnis, indem wir den Test durchführen:

79² + 15 = 6241 + 15 = 6256

Berechne die Quadratwurzel aus: 7 26 75

Lösung:

 Wir teilen die Zahlen in Zweiergruppen auf, beginnend von rechts

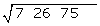
Mit der ersten Ziffer (7) berechnen wir die Zahl, die dem Quadrat der Ziffer am nächsten kommt; sie darf nicht größer sein als die Ziffer

2² < 2 < 3², also nehmen wir 2

Diese Zahl (2) schreiben wir in das Kästchen. Sie ist die 1. Ziffer der Wurzel

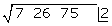
Das Quadrat der erhaltenen Zahl (2²) wird von der ersten Ziffer subtrahiert

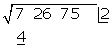
Hinter den Rest schreiben wir die nächste Zifferngruppe des Radikanden (26). Wir trennen die erste Ziffer rechts (6) von der gebildeten Zahl ab und teilen den Rest (32) durch das Doppelte der Zahl im Kästchen, also durch 2 · 2=4

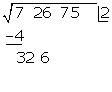
32 : 4 = 8

Unter das Kästchen setzen wir ein weiteres Kästchen mit dem erhaltenen Doppelten (2), gefolgt vom Quotienten der Division (8), und die gebildete Zahl wird mit dem erhaltenen Quotienten (8) multipliziert

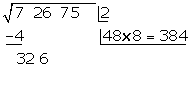
Da diese Zahl größer ist als der Rest (326), müssen wir mit kleineren Zahlen probieren, bis das Produkt kleiner ist als der Rest

47 · 7 = 329

46 · 6 = 276

Bei 6 ist das Ergebnis kleiner als der Rest, also schreiben wir die 6 als zweite Ziffer der Wurzel

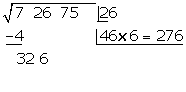
Wir subtrahieren das erhaltene Produkt (276) vom Rest (326)

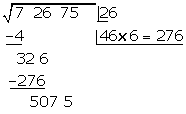
Hinter den Rest schreiben wir die nächste Zifferngruppe des Radikanden (75). Wir trennen die erste Ziffer rechts (5) von der gebildeten Zahl ab und teilen den Rest (507) durch das Doppelte der Zahl im Kästchen, also durch 2 · 26=52

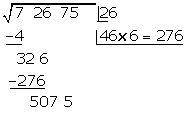
507 : 52 = 9,75    Wir probieren mit 9

Unter das Kästchen setzen wir ein weiteres Kästchen mit dem erhaltenen Doppelten (52), gefolgt vom Quotienten der Division (9), und die gebildete Zahl wird mit dem erhaltenen Quotienten (9) multipliziert

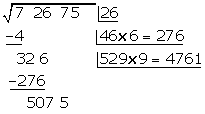
Mit 9 ist das Ergebnis kleiner als der Rest, also schreiben wir 9 als dritte Ziffer der Wurzel

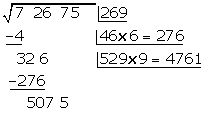
Wir subtrahieren das erhaltene Produkt (4761) vom Rest (5075)

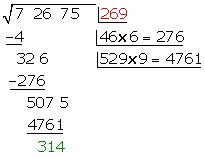
Somit ist 269 die Wurzel und 314 der Rest.

Wir überprüfen das Ergebnis, indem wir den Test durchführen:

269² + 314 = 72 361 + 314 = 72675

Berechne die Quadratwurzel aus: 

264.315

Lösung:

Berechne die Quadratwurzel aus:

72675,687

Lösung:
Wir befolgen die gleichen Schritte wie in den vorherigen Übungen.