Die statistische Inferenz ist die Gesamtheit der Methoden und Techniken, die es ermöglichen, aus den empirischen Informationen einer Stichprobe auf das Verhalten einer bestimmten Grundgesamtheit mit einem messbaren Fehlerrisiko in Bezug auf die Wahrscheinlichkeit zu schließen.
Einige Beispiele für die Verwendung der Inferenzstatistik finden sich in folgenden Bereichen
- Umfragen zum Wahltrend
- Marktanalyse
- Epidemiologie in der Medizin
- Klimaforschung
Stichprobe
Eine bestimmte Kette von Einkaufszentren beschäftigt 150 Mitarbeiter in der Personalabteilung, 450 in der Verkaufsabteilung, 200 in der Buchhaltung und 100 im Kundendienst. Für die Durchführung einer Mitarbeiterbefragung muss eine Stichprobe von 180 Arbeitnehmern ausgewählt werden.
Welche Art von Stichprobe sollten wir für die Auswahl der Stichprobe verwenden, wenn wir möchten, dass sie Beschäftigte aus den vier oben genannten Abteilungen umfasst?
Wie viele Mitarbeiter sollten wir proportional in jeder Abteilung auswählen?
1 Welche Art von Stichprobe sollten wir für die Auswahl der Stichprobe verwenden, wenn wir möchten, dass sie Beschäftigte aus den vier oben genannten Abteilungen umfasst?Wir werden eine geschichtete Zufallsstichprobe verwenden. Da wir Vertreter aus jeder Abteilung haben wollen, nehmen wir eine aussagekräftige Stichprobe, die den Anteil der Mitarbeiter in jeder Abteilung repräsentiert.
2 Wie viele Mitarbeiter sollten wir proportional in jeder Abteilung auswählen?
Um eine proportionale Anzahl aus jeder Abteilung zu wählen, müssen wir zunächst den Anteil kennen, den die Stichprobengröße im Verhältnis zur Gesamtzahl der Arbeitnehmer haben wird. Das heißt:
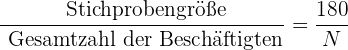
wobei
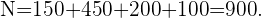
Nun muss die Anzahl der aus jeder Abteilung auszuwählenden Beschäftigten das von uns berechnete Verhältnis einhalten, d.h. die Anzahl  der Beschäftigten in jeder Abteilung muss stimmen:
der Beschäftigten in jeder Abteilung muss stimmen:
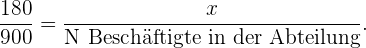
Wir berechnen

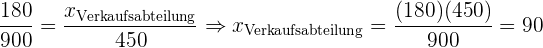
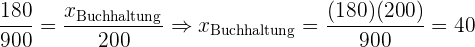

Wir überprüfen:
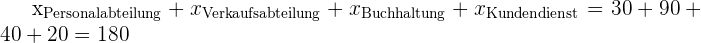 ,
,
was exakt dem Umfang der Stichprobe entspricht.
Stichprobe
In einem bestimmten Viertel soll eine Studie durchgeführt werden, um mehr über die Art der Freizeitaktivitäten zu erfahren, die die Bewohner am liebsten mögen. Zu diesem Zweck werden 100 zufällig ausgewählte Personen befragt.
Erkläre, welches Auswahlverfahren besser geeignet wäre: Zufallsstichprobe mit oder ohne Zurücklegen. Weshalb?
Da sich die Präferenzen mit dem Alter ändern und bekannt ist, dass in der Nachbarschaft 2.500 Kinder, 7.000 Erwachsene und 500 ältere Menschen leben, wird beschlossen, die oben genannte Stichprobe anhand einer geschichteten Stichprobe mit proportionaler Verteilung auszuwählen. Bestimme den Stichprobenumfang für jede Schicht.
1 Erkläre, welches Auswahlverfahren besser geeignet wäre: Zufallsstichprobe mit oder ohne Zurücklegen. Weshalb?Da die Grundgesamtheit endlich ist, können wir die Formeln, die wir untersucht haben, für die Zufallsstichprobe mit Zurücklegen verwenden.
Eine Stichprobe ohne Zurücklegen ist jedoch möglich, mit dem einzigen Nachteil, dass die Berechnungen etwas komplizierter sind.
2 Da sich die Präferenzen mit dem Alter ändern und bekannt ist, dass in der Nachbarschaft 2.500 Kinder, 7.000 Erwachsene und 500 ältere Menschen leben, wird beschlossen, die oben genannte Stichprobe anhand einer geschichteten Stichprobe mit proportionaler Verteilung auszuwählen. Bestimme den Stichprobenumfang für jede Schicht.
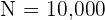 ist die Größe der Grundgesamtheit und
ist die Größe der Grundgesamtheit und 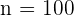 die Größe der Stichprobe. Wir bezeichnen
die Größe der Stichprobe. Wir bezeichnen 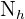 die Größe der Schicht
die Größe der Schicht  und
und  als Größe der Stichprobe, die wir aus
als Größe der Stichprobe, die wir aus  nehmen. Bei der geschichteten Stichprobe mit proportionaler Zuordnung gilt, dass
nehmen. Bei der geschichteten Stichprobe mit proportionaler Zuordnung gilt, dass
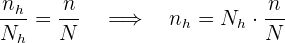
Deshalb müssen wir die Werte  für jede Schicht bestimmen. Die Größen jeder Schicht sind:
für jede Schicht bestimmen. Die Größen jeder Schicht sind: 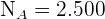 (Kinder),
(Kinder),  (Erwachsene) und
(Erwachsene) und 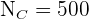 (ältere Menschen).
(ältere Menschen).
Die Stichprobengröße der Kinder ist:
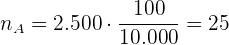
Die Stichprobengröße der Erwachsenen ist:
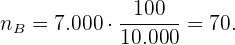
Die Stichprobengröße der älteren Menschen ist:
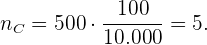
Wir stellen fest, dass die Stichprobengrößen ingesamt 100 ergeben:
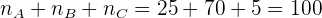
Konfidenzintervall
Die Hämoglobinmenge im Blut des Menschen folgt einer Normalverteilung mit einer Standardabweichung von 2 g/dl. Berechne das Konfidenzniveau für eine Stichprobe von 12 Blutentnahmen, die darauf hinweist, dass der mittlere Hämoglobinwert der Bevölkerung zwischen 13 und 15 g/dl liegt.
Wir müssen das Konfidenzniveau für den mittleren Hämoglobinwert im Blut zwischen 13 und 15 g/dl ermitteln. Um dies festzustellen, müssen wir das Signifikanzniveau kennen. Dieses kann durch die Formel für den Standardfehler ermittelt werden, die lautet es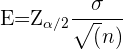 .
.  ist hierbei die Standardabweichung,
ist hierbei die Standardabweichung,  ist die Größe der Stichprobe und
ist die Größe der Stichprobe und  ist der Wert Z einer Standardnormalverteilung
ist der Wert Z einer Standardnormalverteilung 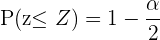 . Da wir wissen wollen, wie zuverlässig der Mittelwert zwischen 13 und 15 g/dl liegt, nehmen wir dieses Intervall als Schätzwert für den Standardfehler und setzen die Werte in die folgende Formel ein und erhalten
. Da wir wissen wollen, wie zuverlässig der Mittelwert zwischen 13 und 15 g/dl liegt, nehmen wir dieses Intervall als Schätzwert für den Standardfehler und setzen die Werte in die folgende Formel ein und erhalten 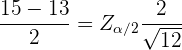
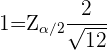 wir bestimmen
wir bestimmen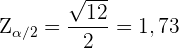 . Da wir den Wert für
. Da wir den Wert für  bereits kennen, können wir die entsprechende Wahrscheinlichkeit berechnen. Früher wurden dafür Tabellen verwendet, heute gibt es einfachere Werkzeuge. Die Wahrscheinlichkeit beträgt also
bereits kennen, können wir die entsprechende Wahrscheinlichkeit berechnen. Früher wurden dafür Tabellen verwendet, heute gibt es einfachere Werkzeuge. Die Wahrscheinlichkeit beträgt also 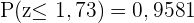 . Nachdem wir
. Nachdem wir  berechnet haben, müssen wir die Wahrscheinlichkeit vom linken Extremwert der Normalverteilung subtrahieren:
berechnet haben, müssen wir die Wahrscheinlichkeit vom linken Extremwert der Normalverteilung subtrahieren: 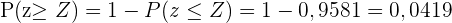 und somit
und somit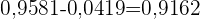 , Daher beträgt das Konfidenzniveau, dass der mittlere Hämoglobinwert zwischen 15 und 13 g/dl liegt, bei einer Stichprobe von 12 Blutentnahmen 91,62 %.
, Daher beträgt das Konfidenzniveau, dass der mittlere Hämoglobinwert zwischen 15 und 13 g/dl liegt, bei einer Stichprobe von 12 Blutentnahmen 91,62 %.
Der monatliche Umsatz eines Haushaltswarengeschäfts folgt einer Normalverteilung mit einer Standardabweichung von 900 €. In einer statistischen Erhebung über die Verkäufe der letzten neun Monate wurde ein Konfidenzintervall für den monatlichen Durchschnittsumsatz ermittelt, dessen Extremwerte bei 4.663 € und 5.839 € liegen. Wie hoch war der durchschnittliche Umsatz in diesen neun Monaten?
Wie lautet das Konfidenzniveau für dieses Intervall?
1 Wie hoch war der durchschnittliche Umsatz in diesen neun Monaten?Bei der Berechnung des Konfidenzintervalls für den Mittelwert einer Normalverteilung liegt der Mittelwert immer in der Mitte des Intervalls. Der Mittelwert ist daher
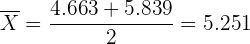
Der Mittelwert lag also bei 5.251 €.
2 Wie lautet das Konfidenzniveau für dieses Intevall?
Es gilt, dass  ,
, 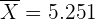 und
und 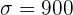 . Daraus folgt, dass die Untergrenze mit Hilfe folgender Formel berechnet wird
. Daraus folgt, dass die Untergrenze mit Hilfe folgender Formel berechnet wird
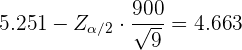
Das heißt:
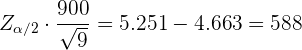
Deshalb:
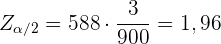
Daraus ergibt sich, dass 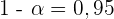 . Das Konfidenzniveau lag also bei 95%.
. Das Konfidenzniveau lag also bei 95%.
Die Zeit, die die Mitarbeiter an der Kasse in einem Supermarkt benötigen, um die Zahlung abzuwickeln, folgt einer Normalverteilung mit unbekanntem Mittelwert und einer Standardabweichung von 0,5 Minuten. Bei einer Stichprobe von 25 Kunden wurde eine durchschnittliche Zeit von 5,2 Minuten ermittelt.
Berechne das Konfidenzintervall auf dem Niveau von 95 % für die durchschnittliche Zeit, die benötigt wird, um die Zahlungen der Kunden abzuwickeln. Gib die Stichprobengröße an, die erforderlich ist, um diese durchschnittliche Zeit mit einem Fehler von 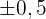 und einem Konfidenzniveau von 95 % zu schätzen.
und einem Konfidenzniveau von 95 % zu schätzen.
1 Berechne das Konfidenzintervall auf dem Niveau von 95 % für die durchschnittliche Zeit, die benötigt wird, um die Zahlungen der Kunden abzuwickeln.Da die Stichprobe aus 25 Kunden besteht, wird zur Berechnung des Konfidenzintervalls die folgende Formel verwendet:
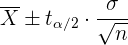
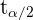 ist hierbei der kritische Wert und
ist hierbei der kritische Wert und 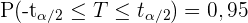 , wobei
, wobei  eine Zufallsvariable ist, die einer studentischen t-Verteilung mit einem Freiheitsgrad von 24 folgt.
eine Zufallsvariable ist, die einer studentischen t-Verteilung mit einem Freiheitsgrad von 24 folgt.
Den Wert für 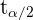 können wir einer t-Verteilungstabelle entnehmen oder eine entsprechende Software nutzen. Das Ergebnis ist
können wir einer t-Verteilungstabelle entnehmen oder eine entsprechende Software nutzen. Das Ergebnis ist 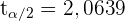
Somit ist das Konfidenzintervall
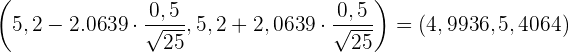
2 Gib die Stichprobengröße an, die erforderlich ist, um diese durchschnittliche Zeit mit einem Fehler von 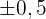 und einem Konfidenzniveau von 95 % zu schätzen.
und einem Konfidenzniveau von 95 % zu schätzen.
Um die Stichprobengröße zu ermitteln, ersetzen wir 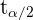 durch
durch  , die einer Standardnormalverteilung entstammt. Da der Fehler
, die einer Standardnormalverteilung entstammt. Da der Fehler 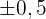 sein muss, gilt
sein muss, gilt
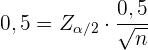 ,
,
wobei 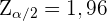 . Wenn wir
. Wenn wir  bestimmen, erhalten wir somit
bestimmen, erhalten wir somit
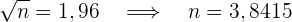
Das heißt, dass die Stichprobengröße mindestens  sein muss.
sein muss.
Hypothesentest mit zwei Schwellenwerten
Ein Hersteller von Lampen testet ein neues Produktionsverfahren, das als akzeptabel gilt, wenn die nach diesem Verfahren hergestellten Lampen eine normale Grundgesamtheit mit einer durchschnittlichen Lebensdauer von 2400 Stunden und einer Standardabweichung von 300 Stunden ergeben. Eine Stichprobe von 100 Lampen, die mit diesem Verfahren hergestellt wurden, hat eine durchschnittliche Lebensdauer von 2320 Stunden. Kann die Hypothese der Eignung des neuen Herstellungsverfahrens mit einem Risiko von 5 % oder weniger akzeptiert werden?
In dieser Aufgabe müssen wir einen Hypothesentest durchführen. Ziel ist es, herauszufinden, ob die entnommene Stichprobe ausreicht, um festzustellen, dass das neue Produktionsverfahren zu Lampen mit einer mittleren Lebensdauer von 2400 Stunden und einer Standardabweichung von 300 Stunden führt, die mit einer Wahrscheinlichkeit von 5 % (oder weniger) diese Eigenschaft nicht erfüllen. Der erste Schritt besteht darin, die Nullhypothese ( ) und die Alternativhypothese (
) und die Alternativhypothese ( ) aufzustellen, wobei das Ergebnis in der Regel dazu führt, dass die Nullhypothese abgelehnt oder nicht abgelehnt wird.
) aufzustellen, wobei das Ergebnis in der Regel dazu führt, dass die Nullhypothese abgelehnt oder nicht abgelehnt wird. 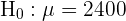
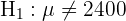
Um den Hypothesentest durchzuführen, müssen wir unsere Statistik berechnen; Da wir davon ausgehen, dass die Lebensdauer gemäß einer Normalverteilung verteilt ist und der Stichprobenumfang gleich 100 ist, nutzen wir die Z-Statistik (Zufallsvariable einer Standardnormalverteilung). Das heißt: 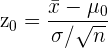 , wobei
, wobei  der Stichprobenmittelwert,
der Stichprobenmittelwert, 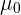 der Mittelwert von
der Mittelwert von  ,
,  die Standardabweichung und
die Standardabweichung und  der Stichprobenumfang ist. Setzt man die Werte ein, so erhält man
der Stichprobenumfang ist. Setzt man die Werte ein, so erhält man 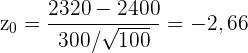 .
.
Nun berechnen wir den p-Wert für 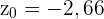 . Da die Alternativhypothese das Gegenteil (
. Da die Alternativhypothese das Gegenteil ( ) besagt, handelt es sich um eine Analyse von zwei Schwellenwerten, für die der p-Wert wie folgt berechnet wird:
) besagt, handelt es sich um eine Analyse von zwei Schwellenwerten, für die der p-Wert wie folgt berechnet wird:
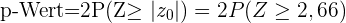
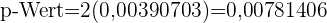
Die Irrtumswahrscheinlichkeit beträgt 5 %, was bedeutet, dass das Signifikanzniveau 0,05 beträgt und wir einen p-Wert von 0,0078 haben; die Nullhypothese wird abgelehnt, wenn der p-Wert kleiner als der Signifikanzwert ist, was hier der Fall ist 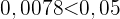 . Daher gibt es genügend Beweise, um die Hypothese abzulehnen, dass die neue Produktionsmethode zu Lampen mit einer mittleren Lebensdauer von 2400 Stunden und einer Standardabweichung von 300 Stunden führen wird, wobei die Wahrscheinlichkeit, dass sie falsch ist, 5 % beträgt.
. Daher gibt es genügend Beweise, um die Hypothese abzulehnen, dass die neue Produktionsmethode zu Lampen mit einer mittleren Lebensdauer von 2400 Stunden und einer Standardabweichung von 300 Stunden führen wird, wobei die Wahrscheinlichkeit, dass sie falsch ist, 5 % beträgt.
Die Qualitätskontrolle einer Akkufabrik hat den Verdacht, dass bei der Produktion eines Akkumodells für Mobiltelefone Fehler aufgetreten sind, die die Laufzeit des Akkus verkürzen. Bislang folgte die Laufzeit einer Normalverteilung mit einem Mittelwert von 300 Gesprächsminuten und einer Standardabweichung von 30 Minuten. Die Prüfung der letzten produzierten Charge vor der Auslieferung ergab jedoch, dass bei einer Stichprobe von 60 Akkus die durchschnittliche Gesprächszeit 290 Minuten betrug. Angenommen, diese Zeit bleibt normal mit der gleichen Standardabweichung: Kann man bei einem Signifikanzniveau von 1 % davon ausgehen, dass der Verdacht der Qualitätskontrolle zutrifft?
Bei dieser Aufgabe müssen wir einen Hypothesentest durchführen. Ziel ist es, herauszufinden, ob die entnommene Stichprobe ausreicht, um mit einer Irrtumswahrscheinlichkeit von 1 % zu bestätigen, dass der Verdacht des Qualitätskontrollteams in Bezug auf die Verschlechterung der Qualität der Akkus zutrifft. Der erste Schritt besteht darin, die Nullhypothese ( ) und die Alternativhypothese (
) und die Alternativhypothese ( ), aufzustellen, wobei das Ergebnis in der Regel dazu führt, dass die Nullhypothese widerlegt oder nicht widerlegt wird.
), aufzustellen, wobei das Ergebnis in der Regel dazu führt, dass die Nullhypothese widerlegt oder nicht widerlegt wird.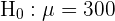
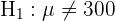
Um den Hypothesentest durchzuführen, müssen wir unsere Statistik berechnen. Da wir davon ausgehen, dass die Laufzeit gemäß einer Normalverteilung verteilt ist und der Stichprobenumfang gleich 60 ist, werden wir die Z-Statistik (Zufallsvariable einer Standardnormalverteilung) anwenden: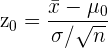
 ist der Mittelwert der Stichprobe,
ist der Mittelwert der Stichprobe, 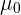 der Mittelwert von
der Mittelwert von  ,
,  die Standardabweichung und
die Standardabweichung und  der Stichprobenumfang. Wir setzen die Werte ein und erhalten
der Stichprobenumfang. Wir setzen die Werte ein und erhalten 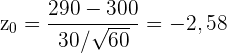 Nun berechnen wir den p-Wert für
Nun berechnen wir den p-Wert für 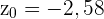 .
.
Da die Alternativhypothese das Gegenteil ( ) besagt, handelt es sich um eine Analyse von zwei Schwellenwerten, für die der p-Wert wie folgt berechnet wird
) besagt, handelt es sich um eine Analyse von zwei Schwellenwerten, für die der p-Wert wie folgt berechnet wird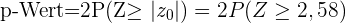
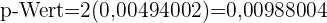
Die Irrtumswahrscheinlichkeit beträgt 1 %, was bedeutet, dass das Signifikanzniveau bei 0,01 liegt und der p-Wert 0,0098 beträgt;die Nullhypothese wird abgelehnt, wenn der p-Wert kleiner als der Signifikanzwert ist, was hier der Fall ist 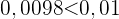
Daher gibt es genügend Beweise, um die Hypothese, dass die durchschnittliche Akkulaufzeit 300 Minuten mit einer Standardabweichung von 30 Minuten beträgt, mit einer Wahrscheinlichkeit von 1 % bei einer Stichprobengröße von 60 abzulehnen. Wir kommen also zu dem Schluss, dass die Vermutungen der Qualitätskontrolle zutreffen.
Man geht davon aus, dass der mittlere Prothrombin-Spiegel bei einer Bevölkerung bei 20 mg/100 ml Plasma liegt, mit einer Standardabweichung von 4 Milligramm/100 ml. Um dies zu überprüfen, wird eine Probe von 40 Personen genommen, bei der der Mittelwert 18,5 mg/100 ml beträgt. Kann die Hypothese mit einem Signifikanzniveau von 5 % akzeptiert werden?
Bei dieser Aufgabe müssen wir einen Hypothesentest durchführen. Ziel ist es, herauszufinden, ob die Stichprobe ausreicht, um mit einer Irrtumswahrscheinlichkeit von 5 % zu behaupten, dass der mittlere Prothrombinspiegel 20 mg/100 ml Plasma mit einer Standardabweichung von 4 mg/100 ml beträgt. Der erste Schritt besteht darin, die Nullhypothese ( ) und die Alternativhypothese (
) und die Alternativhypothese ( ) aufzustellen, wobei das Ergebnis in der Regel dazu führt, dass die Nullhypothese abgelehnt oder nicht abgelehnt wird.
) aufzustellen, wobei das Ergebnis in der Regel dazu führt, dass die Nullhypothese abgelehnt oder nicht abgelehnt wird.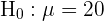
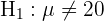
Um den Hypothesentest durchzuführen, müssen wir unsere Statistik berechnen. Da wir davon ausgehen, dass die Prothrombin-Konzentration gemäß einer Normalverteilung verteilt ist und der Stichprobenumfang gleich 40 ist, verwenden wir die Z-Statistik (Zufallsvariable einer Standardnormalverteilung), die wie folgt lautet: 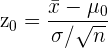 .
.
 ist der Mittelwert der Stichprobe,
ist der Mittelwert der Stichprobe, 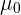 der Mittelwert von
der Mittelwert von  ,
,  die Standardabweichung und
die Standardabweichung und  ist der Stichprobenumfang. Wir setzen die Werte ein und erhalten
ist der Stichprobenumfang. Wir setzen die Werte ein und erhalten 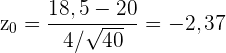 .
.
Nun berechnen wir den p-Wert für 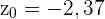 . Da die Alternativhypothese das Gegenteil (
. Da die Alternativhypothese das Gegenteil ( ) besagt, handelt es sich um eine Analyse von zwei Schwellenwerten, für die der p-Wert wie folgt berechnet wird:
) besagt, handelt es sich um eine Analyse von zwei Schwellenwerten, für die der p-Wert wie folgt berechnet wird: 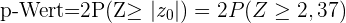
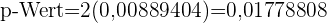
Die Irrtumswahrscheinlichkeit beträgt 5 %, d. h. das Signifikanzniveau liegt bei 0,05 und der p-Wert bei 0,0177; die Nullhypothese wird abgelehnt, wenn der p-Wert unter dem Signifikanzwert liegt, was hier der Fall ist.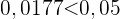
Daher gibt es genügend Beweise, um die Hypothese abzulehnen, dass der mittlere Prothrombin-Spiegel 20 mg/100 ml Plasma mit einer Standardabweichung von 4 mg/100 ml beträgt, bei einem Signifikanzniveau von 5 % und einem Stichprobenumfang von 40.
Mit KI zusammenfassen:



