Die Berechnung der Quadratwurzel von Zahlen kann eine entmutigende Aufgabe sein, wenn man hiefür nicht die richtigen Werkzeuge hat. Zum Glück gibt es verschiedene Methoden, die dir helfen können, die Quadratwurzel von Zahlen zu berechnen, damit du genaue Ergebnisse erhältst. In diesem Artikel erfährst du, wie du die Quadratwurzel von Zahlen mit diesen verschiedenen Methoden berechnen kannst, damit du die für dich beste Methode auswählen kannst.

Schritte zur Berechnung der Quadratwurzel
Um eine Quadratwurzel zu lösen, befolgen wir die Schritte im folgenden Beispiel:
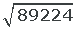
1 Wenn der Radikand aus mehr als zwei Zahlen besteht, werden die Zahlen in Zweiergruppen aufgeteilt, beginnend von rechts.

2 Wir berechnen die ganzzahlige oder exakte Quadratwurzel aus der ersten Zahlengruppe von links, in diesem Fall (8)

Wir stellen uns die Frage: Welche Zahl zum Quadrat ergibt 8?
Wir sehen, dass 8 kein vollständiges Quadrat ist, sondern zwischen zwei vollständigen Quadraten liegt: 4 und 9
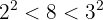
dann nehmen wir die Quadratwurzel des vollständigen Quadrats, das kleiner ist als (8), d.h. die Quadratwurzel von 4, wobei 2 übrig bleibt, und setzen sie in das entsprechende Kästchen.
3 Das Quadrat der erhaltenen Wurzel 2 (d. h. 4) wird von der ersten Zahlengruppe des Radikanden (8) subtrahiert.
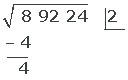
In anderen Worten: Das Quadrat von 2 ist 4. Wir subtrahieren von 8 und erhalten 4.
4 Wir schreiben die zweite Zahlengruppe des Radikanden unter den Strich, trennen die erste Zahl von rechts (2) von der gebildeten Zahl (492) und dividieren den Rest durch das Doppelte der Wurzel 2, also 2(2)=4.

Anders gesagt:
- Wir stellen 92 nach unten und erhalten eine Zahl, mit der wir rechnen können: 492.
- Wir trennen die 1. Zahl von rechts (2) und es bleibt 49.
- Wir dividieren 49 durch das Doppelte der vorher erhaltenen Wurzel 2 · 2 = 4
- Da das Ergebnis von 49 : 4 größer als 9 ist, nehmen wir 9 als Ergebnis
Hinweis: Wir nehmen 9, wenn das Ergebnis der Division (49:4) größer als 9 ist
5 In einer weiteren Zeile unter der Wurzel platzieren wir das Doppelte dieser Wurzel (4) sowie den Quotienten, den wir erhalten (9). Schließlich multiplizieren wir die erhaltene Zahl (49) mit dem Quotienten (9). Danach subtrahieren wir (441) von der Zahl (492) des Radikanden.

- In eine weitere Zeile schreiben wir das Doppelte der Wurzel, was in diesem Fall 4 ist.
- Wir schreiben den erhaltenen Quotienten (9) hinter die 4 und erhalten so die Zahl 49.
- Wir multiplizieren 49 mit 9 und erhalten 441.
- Wir subtrahieren 441 von 492.
Hinweis: Wenn wir einen Wert erhalten hätten, der größer als die berechenbare Menge des Radikanden ist, hätten wir es mit 8, mit 7... versucht, bis wir einen niedrigeren Wert gefunden hätten.
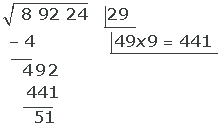
Hinweis: Wenn das Ergebnis von 49 · 9 größer als 492 gewesen wäre, hätten wir 49 · 8, 49 · 7,... gerechnet.
6 Der erhaltene Quotient (9) ist die zweite Zahl unter der Wurzel; der Rest ist (29).
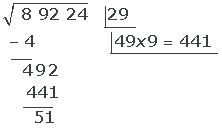
7 Wir holen das darauffolgende Zahlenpaar nach unten und wiederholen die vorhergehenden Schritte.
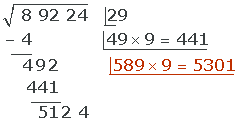
Da 5301 > 5124, probieren wir es mit der Zahl 8.
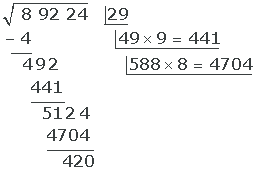
Somit:
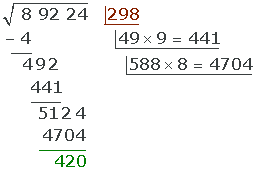
und damit beenden wir unsere Berechnung.
8 Quadratwurzel-Probe. Damit das Ergebnis richtig ist, muss folgende Bedingung erfüllt sein:

Die erhaltenen Werte erfüllen die Bedingung:
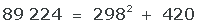
Beispiele mit Quadratwurzeln
Berechne die Quadratwurzeln von:
1 Berechnen
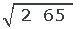
Wir wenden die vorherigen Schritte an und erhalten:

Wir beenden die Berechnung.
2 Berechnen
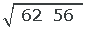
Wir berechnen:
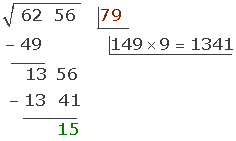
3 Berechnen

Wir berechnen:













