Kapitel
Um einen Bruch zu potenzieren, spielen sowohl der Nenner als auch der Zähler eine Rolle.
,
immer wenn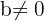 
Beispiel: Berechne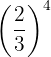 
Potenzierte Brüche mit negativem Exponenten
Eine Potenz eines Bruchs mit negativem Exponenten ist gleich einer anderen Potenz, deren Basis der Kehrwert des ursprünglichen Bruchs ist und die einen positiven Exponenten hat
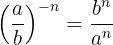
Beispiel: Berechne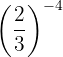 
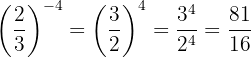
Rechengesetze zu Potenzen von Brüchen
1Jeder Bruch hoch 0 ist gleich 1.
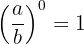
2Jeder Bruch hoch 1 ist gleich demselben Bruch.
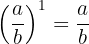
3Das Produkt von Potenzen mit der gleichen Basis ist eine weitere Potenz mit der gleichen Basis, deren Exponent gleich der Summe der Exponenten ist.
4Die Division von Potenzen mit der gleichen Basis ist eine weitere Potenz mit der gleichen Basis, deren Exponent gleich der Differenz der Exponenten ist.
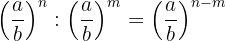
5Die Potenz einer Potenz ist eine andere Potenz mit der gleichen Basis und ihr Exponent ist gleich dem Produkt der Exponenten.
6Das Produkt von Potenzen mit demselben Exponenten ist eine weitere Potenz mit demselben Exponenten, und ihre Basis ist gleich dem Produkt der Basen.
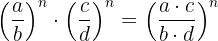
7Der Quotient von Potenzen mit demselben Exponenten ist eine weitere Potenz mit demselben Exponenten, deren Basis gleich dem Quotienten der Basen ist.
Aufgaben mit Lösungen
Vereinfache folgende Rechenoperationen mit Potenzen:
Die Potenzen haben die gleiche Basis, so dass nach Gesetz 3 die Basis die gleiche ist und die Exponenten addiert werden.
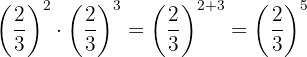
Die Potenzen haben die gleiche Basis, so dass nach Gesetz 3 die Basis die gleiche ist und die Exponenten addiert werden.
Nach Gesetz 2 ist jeder Bruch, der mit 1 potenziert wird, gleich demselben Bruch.
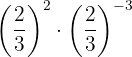
Die Potenzen haben die gleiche Basis, so dass nach Gesetz 3 die Basis die gleiche ist und die Exponenten addiert werden.
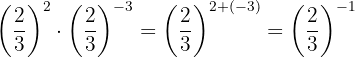
Um das negative Vorzeichen aus dem Exponenten zu entfernen, müssen wir den Kehrbruch schreiben und dann das 2. Gesetz anwenden, das besagt, dass jeder Bruch, der mit 1 potenziert wird, demselben Bruch entspricht.
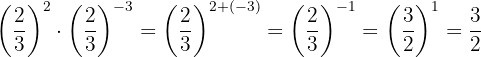
Die Potenzen haben die gleiche Basis, so dass nach Gesetz 3 die Basis die gleiche ist und die Exponenten addiert werden.
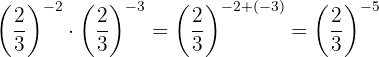
Um das negative Vorzeichen aus dem Exponenten zu entfernen, müssen wir den Kehrbruch schreiben
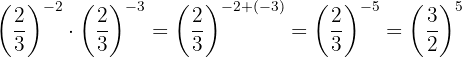
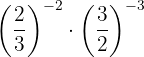
Da die Potenzen nicht die gleiche Basis haben, nehmen wir den Kehrbruch der zweiten Potenz, um einen positiven Exponenten zu erhalten.
Nach Gesetz 2 ist jeder Bruch, der mit 1 potenziert ist, gleich demselben Bruch.
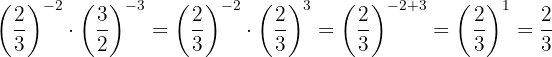
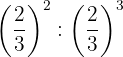
Die Potenzen haben die gleiche Basis, so dass nach Gesetz 4 die Basis die gleiche ist und die Exponenten subtrahiert werden
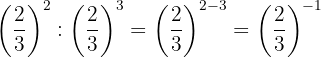
Um das negative Vorzeichen aus dem Exponenten zu entfernen, müssen wir den Kehrbruch schreiben; dann ist nach Gesetz 2 jeder Bruch, der mit 1 potenziert wird, gleich demselben Bruch
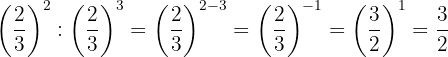
Die Potenzen haben die gleiche Basis, so dass nach Gesetz 4 die Basis die gleiche ist und die Exponenten subtrahiert werden
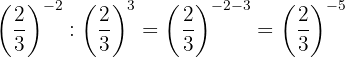
Um das negative Vorzeichen aus dem Exponenten zu entfernen, müssen wir den Kehrbruch schreiben
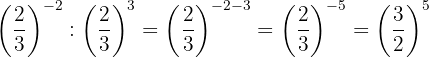
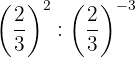
Die Potenzen haben die gleiche Basis, so dass nach Gesetz 4 die Basis die gleiche ist und die Exponenten subtrahiert werden
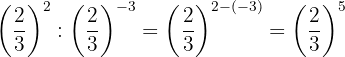
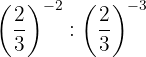
Die Potenzen haben die gleiche Basis, so dass nach Gesetz 4 die Basis die gleiche ist und die Exponenten subtrahiert werden
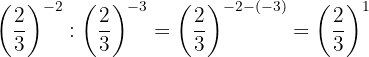
Nach Gesetz 2 ist jeder Bruch, der mit 1 potenziert wird, gleich demselben Bruch
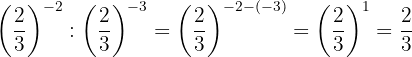
Wir nehmen den Kehrwert der ersten Potenz, um das Vorzeichen des Exponenten zu ändern
Die Potenzen haben die gleiche Basis, so dass nach Gesetz 4 die Basis die gleiche ist und die Exponenten subtrahiert werden
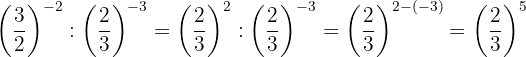
Dies ist die Potenz einer Potenz, so dass durch Gesetz 5 die Basis die gleiche ist und die Exponenten multipliziert werden
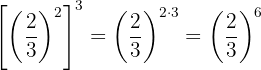
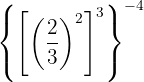
Dies ist die Potenz einer Potenz, so dass durch Gesetz 5 die Basis die gleiche ist und die Exponenten multipliziert werden
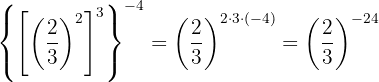
Um das negative Vorzeichen aus dem Exponenten zu entfernen, müssen wir den Kehrbruch schreiben
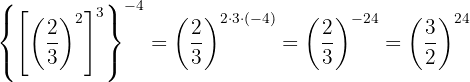
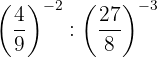
Wir zerlegen die Zahlen in Faktoren und wenden Gesetz 5 der Potenz einer Potenz an
Wir nehmen den Kehrwert der ersten Potenz, um das Vorzeichen des Exponenten zu ändern, und wenden Gesetz 4 des Quotienten von Potenzen an
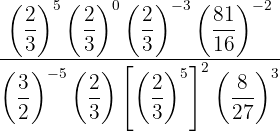
Wir werden versuchen, alle Brüche mit demselben Zähler und Nenner zu bilden, indem wir die Zahlen, die keine Primzahlen sind, in Faktoren zerlegen
Wir haben Elemente, die Potenzen von Potenzen sind, also wenden wir Gesetz 5 an, um sie als eine einzige Potenz zu schreiben
Für die Potenzen mit der Basis 
und negativen Exponenten nehmen wir den Kehrbruch mit positivem Exponenten
Sowohl im Zähler als auch im Nenner multiplizieren wir die Potenzen mit der gleichen Basis unter Verwendung von Gesetz 3 und dividieren die Ergebnisse unter Verwendung von Gesetz 4. Schließlich bilden wir den Kehrbruch mit positivem Exponenten
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
