
Schritte zur Berechnung des gemeinsamen Nenners
Mehrere Brüche auf einen gemeinsamen Nenner zu bringen bedeutet, sie in andere äquivalente Brüche mit dem gleichen Nenner umzuwandeln.
1 Die Nenner werden genommen und in Primzahlen zerlegt.
2 Der gemeinsame Nenner wird bestimmt, der das kleinste gemeinsame Vielfache der Nenner ist.
3 Dieser gemeinsame Nenner wird durch jeden der Nenner dividiert.
4 Der erhaltene Quotient wird in einen Bruch umgewandelt, der gleich 1 ist: 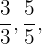 etc.
etc.
5 Wir multiplizieren jeden Bruch mit dem entsprechenden Stammbruch, um den gleichen Nenner zu erhalten.
Beispiele für die Berechnung von Brüchen
1 Finde den kleinsten gemeinsamen Nenner der folgenden Brüche:
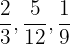
Wir zerlegen jeden der Nenner in Primzahlen:
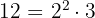

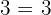
Wir nehmen die Zahlenkombination so, dass keine Zahl fehlt.
In diesem Fall setzt sich das kgV wie folgt zusammen:
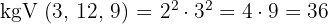
Wir dividieren den gemeinsamen Nenner durch den Nenner jedes Bruchs, um den entsprechenden Stammbruch zu finden:
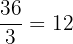
Der Stammbruch, mit dem wir  multiplizieren, ist
multiplizieren, ist 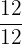 .
.

Der Stammbruch, mit dem wir 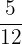 multiplizieren, ist
multiplizieren, ist  .
.

Der Stammbruch, mit dem wir  multiplizieren, ist
multiplizieren, ist 
Wir erhalten:
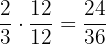
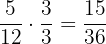
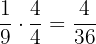
Wenn man alle Brüche auf denselben Nenner bringt, lassen sich Additionen und Subtraktionen leichter durchführen.
2 Finde den kleinsten gemeinsamen Nenner der folgenden Brüche: 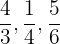 y sumar.
y sumar.
Wir zerlegen jeden der Nenner in Primzahlen:
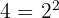
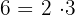
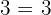
Wir nehmen die Zahlenkombination so, dass keine Zahl fehlt.
In diesem Fall setzt sich das kgV wie folgt zusammen:
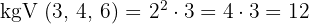
Wenn man alle Brüche auf denselben Nenner bringt, lassen sich Additionen und Subtraktionen leichter durchführen.
Um die Summe der drei Brüche zu berechnen, bringen wir sie zunächst auf den gleichen Nenner  , indem wir jeden einzelnen mit dem entsprechenden Stammbruch multiplizieren:
, indem wir jeden einzelnen mit dem entsprechenden Stammbruch multiplizieren:
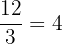
Der Stammbruch, mit dem wir  multiplizieren, ist
multiplizieren, ist 
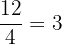
Der Stammbruch, mit dem wir  multiplizieren, ist
multiplizieren, ist 
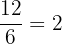
Der Stammbruch, mit dem wir  multiplizieren, ist
multiplizieren, ist 
Wir berechnen:


Mit KI zusammenfassen:












