Kapitel

Grundlegenden Definitionen
Gemischte Zahl
Um eine gemischte Zahl in einen unechten Bruch umzuwandeln, bleibt der Nenner gleich und der Zähler ist die Summe des Produkts aus der ganzen Zahl und dem Nenner plus dem Zähler der gemischten Zahl.
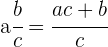
Gleichwertige Brüche
Zwei Brüche sind gleichwertig, wenn Folgendes gilt:
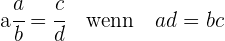
Brüche gleichnamig machen
1 Wir ermitteln den gemeinsamen Nenner determina el denominador común, der das kleinste gemeinsame Vielfache der Nenner ist.
2 Dieser gemeinsame Nenner wird durch jeden der Nenner geteilt und der erhaltene Quotient mit dem entsprechenden Zähler multipliziert.
Addition und Subtraktion von Brüchen
Brüche mit gleichem Nenner
Die Zähler werden addiert oder subtrahiert, der Nenner bleibt unverändert.


Brüche mit unterschiedlichem Nenner
Zunächst werden die Nenner auf einen gemeinsamen Nenner gebracht und die Zähler der erhaltenen gleichwertigen Brüche addiert oder subtrahiert. 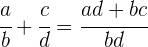
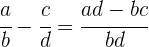
Multiplikation von Brüchen
Das Produkt zweier Brüche ist ein weiterer Bruch mit:
Der Zähler ist das Produkt der Zähler.
Der Nenner ist das Produkt der beiden Nenner.
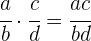
Division von Brüchen
Der Quotient aus zwei Brüchen ist ein weiterer Bruch mit:
Der Zähler ist das Produkt aus Zähler und Nenner.
Der Nenner ist das Produkt aus Nenner und Zähler.

Potenz von Brüchen
Im Folgenden sehen wir, wie sich Brüche zur Potenz verhalten.
Erstens: Die Potenz eines Bruchs ist der Bruch zwischen der Potenz des Zählers und der Potenz des Nenners: 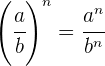
Dies gilt auch für negative Potenzen, wobei jedoch die Reihenfolge von Zähler und Nenner geändert wird: 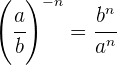
Wenn 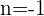 , gilt
, gilt 
Eigenschaften
Im Folgenden sehen wir, wie sich Potenzen von Brüchen bei grundlegenden Rechenoperationen verhalten.
Erstens: Da die Potenz eines Bruchs nur der Bruch der Potenz des Zählers geteilt durch die Potenz des Nenners ist, ergibt der Bruch hoch null 1: 
Ein Bruch zur Potenz  ergibt den gleichen Bruch
ergibt den gleichen Bruch 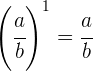
Die Potenzierung und Multiplikation von Brüchen verhält sich genauso wie bei ganzen Zahlen: 
Die Potenzierung und Division von Brüchen verhält sich genauso wie bei ganzen Zahlen: 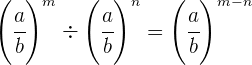
Wenn wir einen Bruch auf eine Potenz und dann auf eine andere Potenz erhöhen, ergibt dies den Bruch, der auf das Produkt der Potenzen erhöht wird: 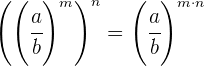
Wenn wir die gleiche Potenz für zwei Brüche haben und dann eine Multiplikation oder Division durchführen, müssen wir die Reihenfolge der Rechenoperationen beachten und zuerst die Potenzierung und dann die entsprechende Operation durchführen.
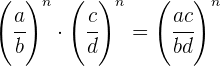
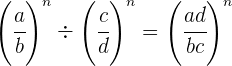
Dezimalbruch
Dezimalzahl in einen Bruch umwandeln
Wenn der Bruch eine Dezimalzahl ist, ist der Zähler des Bruchs die angegebene Zahl ohne Komma und der Nenner die Einheit, gefolgt von so vielen Nullen, wie er Dezimalstellen hat. Einige Beispiele:
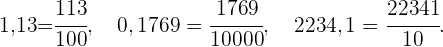
Periodische Zahl in Dezimalbruch umwandeln
Ist der Bruch eine rein periodische Zahl, so hat der resultierende Bruch als Zähler die angegebene Zahl ohne Komma, abzüglich des ganzzahligen Teils, und als Nenner eine Zahl, die aus so vielen Neunen gebildet wird, wie Ziffern in der Periode vorhanden sind. Einige Beispiele:
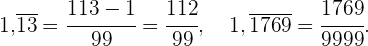
Gemischt periodische Zahl in Dezimalbruch umwandeln
Handelt es sich um eine gemischt periodische Zahl, so hat der resultierende Bruch als Zähler die angegebene Zahl ohne Komma, abzüglich des ganzzahligen Teils, gefolgt von den nichtperiodischen Dezimalziffern, und als Nenner eine Zahl, die aus so vielen Neunen gebildet wird, wie Ziffern in der Periode vorhanden sind, gefolgt von so vielen Nullen, wie Ziffern im nichtperiodischen Dezimalteil vorhanden sind. Hier ein Beispiel
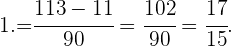
Mit KI zusammenfassen:












