Kapitel

Grundlegende Rechenoperationen mit Brüchen
Drücke jeden der folgenden Brüche in Minuten aus:
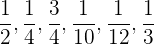
Wir beachten, dass  Stunde
Stunde 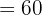 Minuten sind. Daher kann ein einfacher Dreisatz verwendet werden, um jeden Bruch in Minuten umzurechnen.
Minuten sind. Daher kann ein einfacher Dreisatz verwendet werden, um jeden Bruch in Minuten umzurechnen.
1 Umrechnung von  Stunde in Minuten:
Stunde in Minuten:
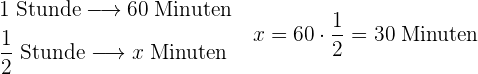
2 Umrechnung von  Stunde in Minuten:
Stunde in Minuten:
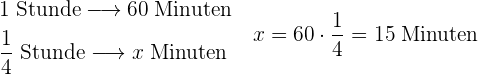
3 Umrechnung von  Stunde in Minuten:
Stunde in Minuten:
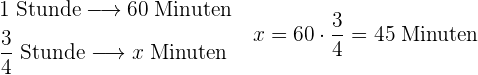
4 Umrechnung von  Stunde in Minuten:
Stunde in Minuten:
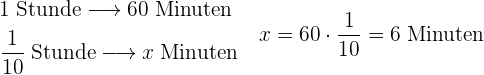
5 Umrechnung von 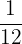 Stunde in Minuten:
Stunde in Minuten:
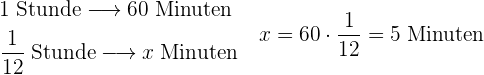
6 Umrechnung von 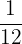 Stunde in Minuten:
Stunde in Minuten:
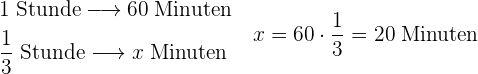
Finde die Paare von gleichwertigen Brüchen und stelle sie in Paaren auf:
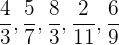
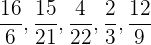
Um diese Aufgabe zu lösen, werden wir aus praktischen Gründen das Kürzen von Brüchen anwenden. Für die Brüche gilt also Folgendes:
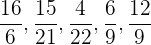 können gekürzt werden.
können gekürzt werden.
1 Wir kürzen den Bruch 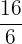 :
:
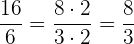
Das entsprechende Paar des Bruchs 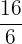 ist
ist  .
.
2 Wir kürzen den Bruch 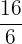 :
:
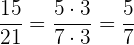
Das entsprechende Paar des Bruchs 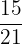 ist
ist  .
.
3 Wir kürzen den Bruch 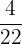 :
:
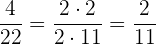
Das entsprechende Paar des Bruchs 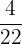 ist
ist 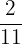 .
.
4 Wir kürzen den Bruch  :
:
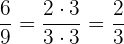
Das entsprechende Paar des Bruchs  ist
ist  .
.
5 Wir kürzen den Bruch 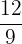 :
:
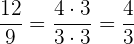
Das entsprechende Paar des Bruchs 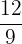 ist
ist  .
.
Schreibe die Kehrwerte von:
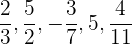
Zunächst ist zu beachten, dass eine Zahl und ihr Kehrwert die Bedingung erfüllen, dass ihr Produkt gleich 1 ist.
1 Für den Kehrwert  von
von  muss gelten, dass
muss gelten, dass 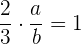 , daher
, daher 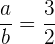 .
.
2 Für den Kehrwert  von
von  debe satisfacer que
debe satisfacer que 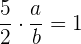 , daher
, daher 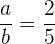 .
.
3 Für den Kehrwert  von
von 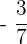 muss gelten, dass
muss gelten, dass 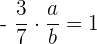 , daher
, daher 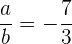 .
.
4 Für den Kehrwert  von
von 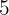 muss gelten, dass
muss gelten, dass 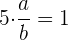 , daher
, daher 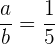 .
.
5 Für den Kehrwert  von
von  muss gelten, dass
muss gelten, dass 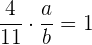 , daher
, daher 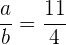 .
.
Vergleiche die gegebenen Brüche und füge entsprechend das Zeichen > oder < ein.
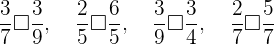
Um diese Aufgabe zu lösen, verwenden wir die folgenden beiden Ergebnisse:
Bei zwei Brüchen mit gleichem Zähler ist derjenige mit dem größeren Nenner kleiner.
Bei zwei Brüchen mit gleichem Nenner ist derjenige mit dem kleineren Zähler kleiner.
Daraus ergibt sich:
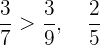
Vergleiche folgende Brüche:
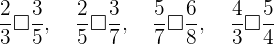
Um diese Aufgabe zu lösen, müssen wir den gemeinsamen Nenner der beiden zu vergleichenden Brüche berechnen. Beachte, daß der Bruch mit dem kleineren Zähler auch der kleinere Bruch ist. Wir erhalten also Folgendes:
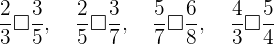
Wenn wir einen gemeinsamen Nenner für jeden der Fälle berechnen, erhalten wir Folgendes:
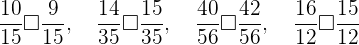
Daher sind die folgenden Ungleichungen erfüllt:
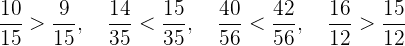
Das heißt:
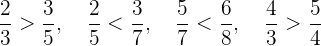
Reihenfolge vom kleinsten zum größten Bruch:
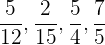
Um die Brüche auf einen gemeinsamen Nenner zu bringen, müssen wir zunächst das kleine Vielfache der Nenner berechnen; derjenige mit dem kleineren Zähler ist kleiner.
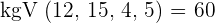
Das kleinste gemeinsame Vielfache 60 sagt uns, dass es sich um eine Zahl handelt, die jeden der Nenner teilt. Wir schreiben jeden der Brüche so um, dass wir einen Bruch erhalten, der den ursprünglichen Brüchen entspricht, aber den Nenner 60 hat:
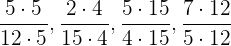
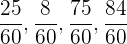
 \begin{equation*}\frac{8}{60}< \frac{25}{60}< \frac{75}{60}< \frac{84}{60}\end{equation*}[/latex]
\begin{equation*}\frac{8}{60}< \frac{25}{60}< \frac{75}{60}< \frac{84}{60}\end{equation*}[/latex]
 \begin{equation*}\frac{2}{15}< \frac{5}{12}< \frac{5}{4}<\frac{7}{5}\end{equation*}[/latex]
\begin{equation*}\frac{2}{15}< \frac{5}{12}< \frac{5}{4}<\frac{7}{5}\end{equation*}[/latex]
Zeige zwei verschiedene Rechenwege auf:
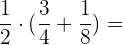
Wir wenden das Distributivgesetz an: 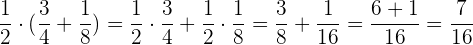 2 Summe:
2 Summe: 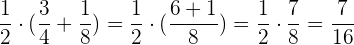
Berechne das Ergebnis jeder der Additionen, indem du die Faktorisierung des gemeinsamen Faktors anwendest.
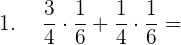
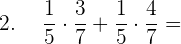
Die Faktorisierung ist die Umkehrung des Distributivgesetzes, d.h. wir können die Addition in ein Produkt umwandeln, indem wir den Faktor ausklammern:
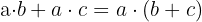
1 Um 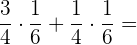 zu berechnen, faktorisieren wir
zu berechnen, faktorisieren wir  und lösen im Anschluss:
und lösen im Anschluss:
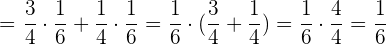
2 Um 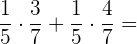 zu berechnen, faktorisiern wir
zu berechnen, faktorisiern wir  und lösen im Anschluss:
und lösen im Anschluss: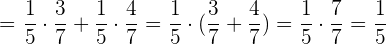
Teile folgende Brüche in echte und unechte Brüche ein: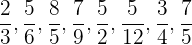
Hierfür müssen wir beachten:
Bei echten Brüchen ist der Nenner größer als der Zähler.
Bei unechten Brüchen ist der Nenner kleiner als der Zähler.
1 Echte Brüche:
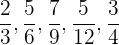
2 Unechte Brüche: 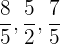
Berechne die Summe der folgenden Brüche:
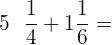
Wir schreiben um und addieren: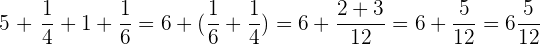
Dezimalausdruck in Bruch umwandeln
Wandle die folgenden Dezimalausdrücke in Brüche um: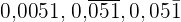
1 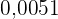 in einen Bruch umwandeln:Da es sich um eine exakte Dezimalzahl handelt, schreiben wir im Zähler die Zahl ohne Komma und im Nenner die Einheit, gefolgt von 4 Nullen, da es 4 Dezimalstellen gibt:
in einen Bruch umwandeln:Da es sich um eine exakte Dezimalzahl handelt, schreiben wir im Zähler die Zahl ohne Komma und im Nenner die Einheit, gefolgt von 4 Nullen, da es 4 Dezimalstellen gibt: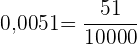
2 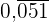 in einen Bruch umwandeln:
in einen Bruch umwandeln:
Da es sich um eine reine periodische Zahl handelt, schreiben wir im Zähler die Zahl ohne Komma und im Nenner 3 Neunen, da es 3 periodische Ziffern gibt: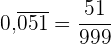 .
.
3 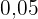 in einen Bruch umwandeln:
in einen Bruch umwandeln:
Da es sich um eine gemischte periodische Zahl handelt, schreiben wir im Zähler die Zahl ohne Komma und subtrahieren den Teil, der außerhalb der Periode steht. Im Nenner stehen eine Neun und zwei Nullen, weil wir eine Ziffer in der Periode haben und es zwei Nachkommastellen gibt: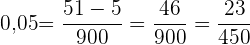
Wandle folgende Dezimalzahlen in Brüche um:
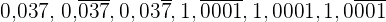
1 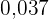 in einen Bruch umwandeln:
in einen Bruch umwandeln:
Da es sich um eine exakte Dezimalzahl handelt, schreiben wir im Zähler die Zahl ohne Komma und im Nenner die Einheit, gefolgt von 3 Nullen, da es 3 Dezimalstellen gibt: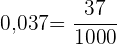
2 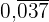 in einen Bruch umwandeln:
in einen Bruch umwandeln:
Da es sich um eine reine periodische Zahl handelt, schreiben wir im Zähler die Zahl ohne Komma und im Nenner 3 Neunen, da es 3 periodische Ziffern gibt.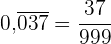
3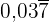 in einen Bruch umwandeln:
in einen Bruch umwandeln:
Da es sich um eine gemischte periodische Zahl handelt, schreiben wir in den Zähler die Zahl ohne Komma minus die Zahlen, die außerhalb der Periode stehen. Im Nenner stehen eine Neun und zwei Nullen, weil wir eine Ziffer im Punkt haben und es zwei Nachkommastellen gibt.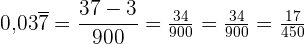
4 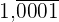 in einen Bruch umwandeln:
in einen Bruch umwandeln:
Da es sich um eine rein periodische Zahl handelt, schreiben wir im Zähler die Zahl ohne Komma abzüglich des Teils, der außerhalb der Periode liegt. Im Nenner stehen 4 Neunen, weil es 4 periodische Ziffern gibt.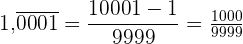
5 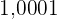 in einen Bruch umwandeln:
in einen Bruch umwandeln:
Da es sich um eine exakte Dezimalzahl handelt, schreiben wir im Zähler die Zahl ohne Komma und im Nenner die Einheit, gefolgt von 4 Nullen, da es 4 Dezimalstellen gibt.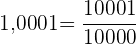
6 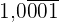 in einen Bruch umwandeln:
in einen Bruch umwandeln:
Da es sich um eine gemischt periodische Zahl handelt, schreiben wir im Zähler die Zahl ohne Komma minus den Teil außerhalb der Periode. Im Nenner stehen 3 Neunen und eine Null, weil wir drei Ziffern in der Periode haben und es eine Nachkommastelle gibt.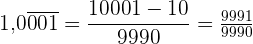
Rechnen mit Brüchen und periodischen Dezimalzahlen
Führe folgende Berechnungen durch:
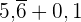
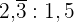
1 Addiere 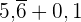 .
.
Zunächst wandeln wir beide Dezimalausdrücke in Brüche um und addieren:
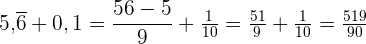
2 Wir berechnen 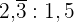
Zunächst wandeln wir beide Dezimalausdrücke in Brüche um und berechnen wie folgt: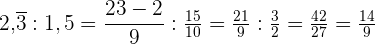
Führe folgende Berechnungen mit Brüchen durch: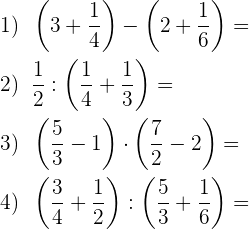
Löse:
1 Wir lösen 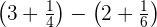 :
:
Wir lösen die Klammern auf. Vor der 2. Klammer steht ein Minuszeichen, wodurch aus dem Plus in der Klammer ein Minus wird.
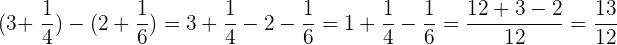
2 Wir lösen 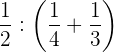
Zuerst addieren wir die Terme innerhalb der Klammer, dann dividieren wir die Brüche und schließlich vereinfachen wir.
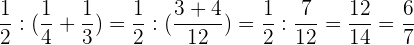
3 Wir lösen 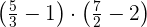
Wir führen folgende Rechenschritte durch und vereinfachen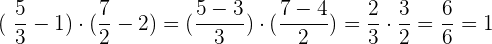
4 Wir lösen 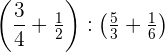 :
:
Wir führen die Rechenschritte innerhalb der Klammern durch, dividieren die Ergebnisse und vereinfachen.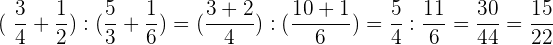
Führe folgende Divisionen durch:
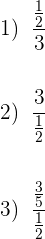
Um jede der Divisionen durchzuführen, denken wir daran, dass die Extremwerte (oben und unten) multipliziert werden. Das Produkt ist der Zähler, während das Produkt der inneren Werte den Nenner bildet. So erhalten wir folgende Ergebnisse:
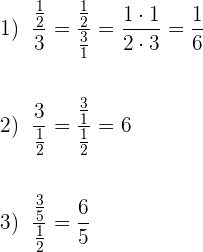
Führe die entsprechenden Rechenschritte durch:
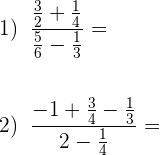
1 Um die Summe 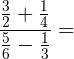 zu berechnen, müssen wir:Die entsprechenden Rechenschritte im Zähler und Nenner durchführen.
zu berechnen, müssen wir:Die entsprechenden Rechenschritte im Zähler und Nenner durchführen.
Den resultierenden Bruch als Division zweier Brüche schreiben, vereinfachen, dividieren und wieder vereinfachen.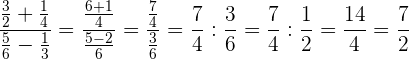
2 Wir addieren 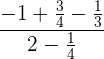 :Wir gehen wie in der vorherigen Aufgabe vor:
:Wir gehen wie in der vorherigen Aufgabe vor: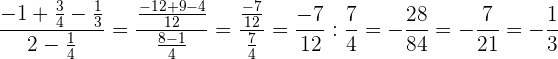 .
.
Führe diese Berechnung durch:
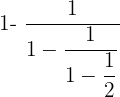
Zunächst berechnen wir 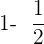
Wir nehmen den Kehrwert von 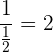 , und erhalten Folgendes:
, und erhalten Folgendes:
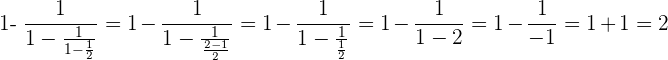
Führe folgende Berechnungen mit Potenzen durch: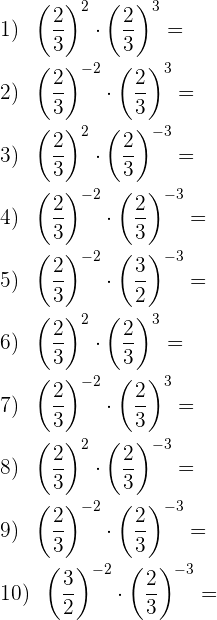
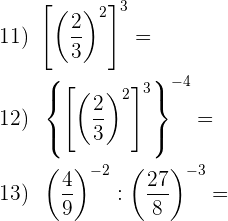
1Für Aufgabe 1) gilt: Wir haben die gleiche Basis und addieren die Potenzen:
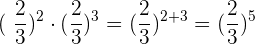
2Für Aufgabe 2) gilt: Wir haben die gleiche Basis und subtrahieren die Potenzen:
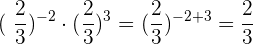
3Für Aufgabe 3) gilt: Wir haben die gleiche Basis und subtrahieren die Potenzen:
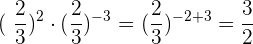
4Für Aufgabe 4) gilt: Wir haben die gleiche Basis und subtrahieren die Potenzen:
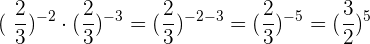
5Bei Aufgabe 5) gehen wir wie folgt vor:
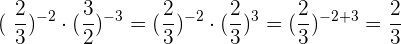
6Bei Aufgabe 6) müssen wir Potenzen mit der gleichen Basis dividieren und subtrahieren die Exponenten:
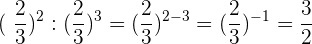
7Bei Aufgabe 7) gehen wir ähnlich wie im vorherigen Beispiel vor:
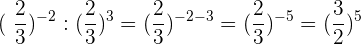
8Bei Aufgabe 8):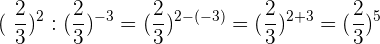
9Bei Aufgabe 9):
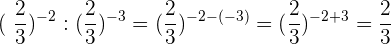
10Bei Aufgabe 10):
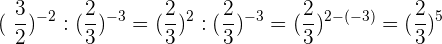
11Bei Aufgabe 11) denken wir daran, dass man zur Multiplikation von Potenzen mit der gleichen Basis die Exponenten multipliziert:
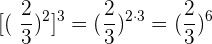
12Bei Aufgabe 12) wenden wir ein ähnliches Verfahren wie in der vorherigen Aufgabe an, wobei wir am Ende den Kehrbruch berücksichtigen, um das Vorzeichen des Exponenten des Bruchs in positiv zu ändern:
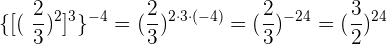
13Bei Aufgabe 13) zerlegen wir die Zahlen in Faktoren, innerhalb jeder Klammer dividieren wir Potenzen mit gleichem Exponenten. Also teilen wir die Basen und lassen den Exponenten gleich:
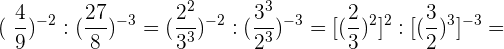
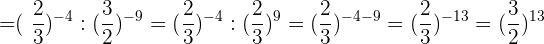
Berechne:
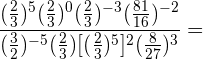
Wir werden versuchen, alle Brüche mit gleichem Zähler und gleichem Nenner zu bilden, indem wir die Zahlen, die keine Primzahlen sind, in Faktoren zerlegen.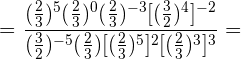
Um von einer Potenz mit negativem Exponenten zu einem positiven Exponenten zu wechseln, müssen wir den Bruch umkehren 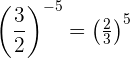 :
: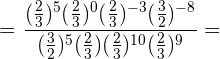
Kehrbruch mit positivem Exponenten: 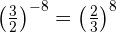 :
: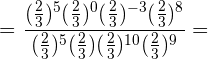
Sowohl im Zähler als auch im Nenner werden die Potenzen mit der gleichen Basis multipliziert und die Ergebnisse dividiert: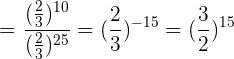
Führe folgende Berechnung durch:
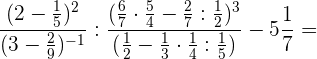
Wir führen die in den Klammern angegebenen Rechenschritte durch und in der Klammer des zweiten Nenners müssen wir zuerst multiplizieren und im nächsten Schritt dividieren. $5 \frac{1}{7}$ ist eine gemischte Zahl, also belassen wir denselben Nenner (7) und der Zähler ist die Summe aus der Multiplikation der ganzen Zahl (5) mit dem Nenner (7) plus dem Zähler der gemischten Zahl (1).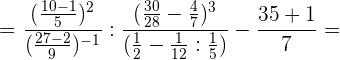
Wir führen die angegebenen Rechenschritte durch und vereinfachen $\frac{30}{28}$: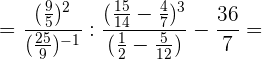
Wir führen die angegebenen Rechenschritte durch und bringen auf einen gemeinsamen Nenner: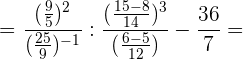
Wir führen beim 2. Bruch die nötigen Rechenschritte durch und vereinfachen: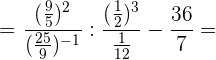
Wir berechnen die Potenzen und bedenken, dass wir bei einem Bruch, der auf eine negative Zahl erhöht wird, den Zähler in den Nenner umwandeln und dann auf den Exponenten erhöhen müssen: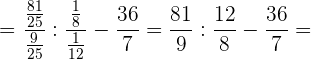
Wir vereinfachen und berechnen: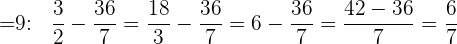
Löse:
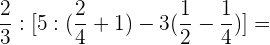
Wir führen in den zwei Klammern die entsprechenden Rechenschritte durch: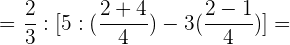
Wir entfernen die eckige Klammer und erhalten: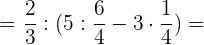
Wir führen die Division und Multiplikation der Klammern durch und vereinfachen die Ergebnisse: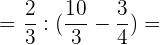
Wir dividieren 2/3 durch das Ergebnis der Klammer und vereinfachen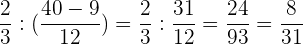
Berechne:
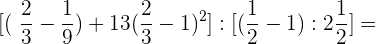
Wir wandeln die gemischte Zahl in einen Bruch um $2 \frac{1}{2}$. Wir belassen den gleichen Nenner (2) und der Zähler ist ist die Summe der Multiplikation des Ganzen (2) mit dem Nenner (2) plus dem Zähler der gemischten Zahl (1). Wir bringen die Brüche jeder Klammer auf einen gemeinsamen Nenner.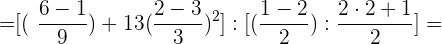
Wir führen die entsprechenden Rechenschritte in den Zählern durch. Innerhalb der 2. eckigen Klammer lösen wir die Klammer auf und aus der eckigen Klammer wird eine runde Klammer: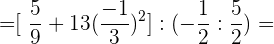
Wir berechnen den Wert der Potenz, und da in der ersten eckigen Klammer keine Klammern mehr vorhanden sind, ersetzen wir sie durch eine Klammer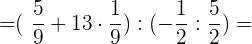
Wir multiplizieren die erste Klammer aus und dividieren in der 2.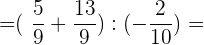
Wir addieren die Summe der ersten Klammer, vereinfachen in der zweiten Klammer und dividieren: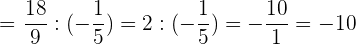
Berechne:
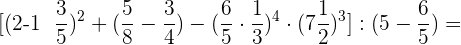
Zunächst rechnen wir mit den Produkten und gemischten Zahlen in den Klammern: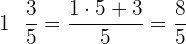
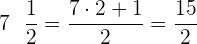
Wir setzen die Ergebnisse ein: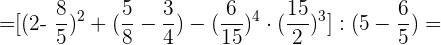
Wir rechnen mit der ersten Klammer, entfernen die zweite, vereinfachen die dritte und rechnen mit der letzten: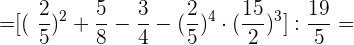
Wir führen das Produkt aus und vereinfachen es, aus der eckigen Klammer wird eine runde Klammer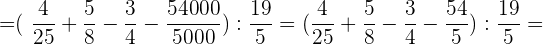
Wir berechnen: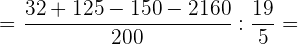
Wir führen die entsprechenden Rechenschritte im Nenner durch, dividieren und vereinfachen das Ergebnis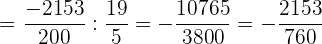
Mit KI zusammenfassen:













