
Wie können Brüche vereinfacht werden?
Einen Bruch zu vereinfachen bedeutet, ihn in einen einfacheren äquivalenten Bruch umzuwandeln.
Um einen Bruch zu vereinfachen, werden Zähler und Nenner durch dieselbe Zahl geteilt.
Wir beginnen mit der Vereinfachung, indem wir die ersten Primzahlen ausprobieren: 2, 3, 5, 7, .... Das heißt, wir versuchen, Zähler und Nenner so lange wie möglich durch 2 zu teilen. Dann gehen wir zu 3 über und so weiter.
Dies wird so lange wiederholt, bis es keine gemeinsamen Teiler mehr gibt.
Beispiel: Vereinfache 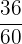
1 Zunächst dividieren wir Zähler und Nenner durch 

2 Der Zähler und der Nenner des erhaltenen Ergebnisses haben wieder die Zahl  als gemeinsamen Teiler
als gemeinsamen Teiler

3 Der neue Zähler und Nenner des erhaltenen Ergebnisses haben die Zahl  als gemeinsamen Teiler
als gemeinsamen Teiler
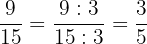
4 Da der neue Zähler und der neue Nenner des erhaltenen Ergebnisses keine gemeinsamen Teiler haben, ist die Vereinfachung von 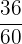 somit
somit  , also
, also
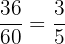
Wenn die Terme des Bruchs auf Nullen enden, streichen wir zunächst die hinteren gemeinsamen Nullen von Zähler und Nenner.
Beispiel: Vereinfache 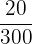
1 Wir dividieren Zähler und Nenner durch 
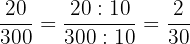
2 Der neue Zähler und der neue Nenner des erhaltenen Ergebnisses haben als gemeinsamen Teiler die Zahl 
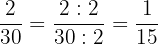
3 Da der neue Zähler und der neue Nenner des Ergebnisses keine gemeinsamen Teiler haben, ist die Vereinfachung von 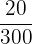 somit
somit 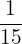 , also
, also
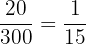
Wenn die Zahl, durch die wir dividieren, der größte gemeinsame Teiler von Zähler und Nenner ist, erhalten wir einen voll gekürzten Bruch.
Beispiel: Vereinfache 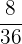
1 Wir dividieren Zähler und Nenner durch den 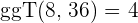
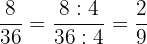
2 Da der neue Zähler und der neue Nenner des erhaltenen Ergebnisses keine gemeinsamen Teiler haben, folgt daraus, dass die Vereinfachung von 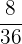 somit
somit  ist, also
ist, also
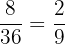
Aufgaben zur Vereinfachung von Brüchen
Vereinfache folgende Brüche
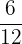
1 Zunächst dividieren wir Zähler und Nenner durch 
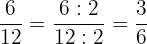
2 Der Zähler und der Nenner des erhaltenen Ergebnisses haben als gemeinsamen Teiler die Zahl 
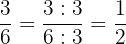
3 Da der neue Zähler und der neue Nenner des erhaltenen Ergebnisses keine gemeinsamen Teiler haben, ist die Vereinfachung von 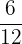 somit
somit  , also
, also
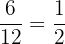
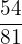
1 Zunächst dividieren wir Zähler und Nenner durch 
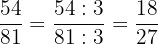
2 Der Zähler und der Nenner des erhaltenen Ergebnisses haben wiederum die Zahl  als gemeinsamen Teiler
als gemeinsamen Teiler
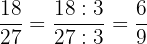
3 Der Zähler und der Nenner des erhaltenen Ergebnisses haben wiederum die Zahl  als gemeinsamen Teiler.
als gemeinsamen Teiler.
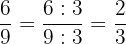
4 Da der neue Zähler und der neue Nenner des erhaltenen Ergebnisses keine gemeinsamen Teiler haben, folgt daraus, dass die Vereinfachung von 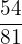 somit
somit  ist, also
ist, also
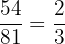
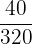
1 Zunächst dividieren wir Zähler und Nenner durch 
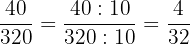
2 Der Zähler und der Nenner des erhaltenen Ergebnisses haben die Zahl  als gemeinsamen Teiler.
als gemeinsamen Teiler.
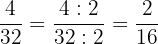
3 Der Zähler und der Nenner des erhaltenen Ergebnisses haben wiederum die Zahl  als gemeinsamen Teiler.
als gemeinsamen Teiler.
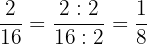
4 Da der neue Zähler und der neue Nenner des erhaltenen Ergebnisses keine gemeinsamen Teiler haben, folgt daraus, dass die Vereinfachung von 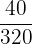 somit
somit  ist, also
ist, also


1 Zunächst dividieren wir Zähler und Nenner durch 
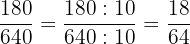
2 Der Zähler und der Nenner des erhaltenen Ergebnisses haben als gemeinsamen Teiler die Zahl 

3 Da der neue Zähler und der neue Nenner des erhaltenen Ergebnisses keine gemeinsamen Teiler haben, folgt daraus, dass die Vereinfachung von  somit
somit  ist, also
ist, also
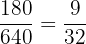

1 Zunächst drücken wir den Zähler und den Nenner als Produkt von Primzahlen aus

2 Um den  der beiden Zahlen zu ermitteln, multiplizieren wir die gemeinsamen Faktoren mit dem niedristen Exponenten
der beiden Zahlen zu ermitteln, multiplizieren wir die gemeinsamen Faktoren mit dem niedristen Exponenten
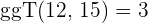
3 Wir dividieren Zähler und Nenner durch den 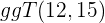

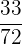
1 Zunächst drücken wir den Zähler und den Nenner als Produkt von Primzahlen aus

2 Um den  der beiden Zahlen zu ermitteln, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
der beiden Zahlen zu ermitteln, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
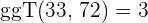
3 Wir dividieren Zähler und Nenner durch den 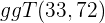

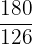
1 Zunächst drücken wir den Zähler und den Nenner als Produkt von Primzahlen aus
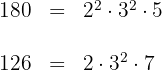
2 Um den  der beiden Zahlen zu ermitteln, multiplizieren wir die gemeinsamen Faktoren mit den niedrigsten Exponenten
der beiden Zahlen zu ermitteln, multiplizieren wir die gemeinsamen Faktoren mit den niedrigsten Exponenten
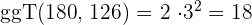
3 Wir dividieren den Zähler und den Nenner durch den 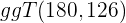
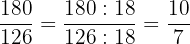
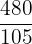
1 Zunächst drücken wir den Zähler und den Nenner als Produkt von Primzahlen aus

2 Um den  der beiden Zahlen zu ermitteln, multiplizieren wir die gemeinsamen Faktoren mit den niedrigsten Exponenten
der beiden Zahlen zu ermitteln, multiplizieren wir die gemeinsamen Faktoren mit den niedrigsten Exponenten
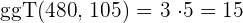
3 Wir dividieren den Zähler und den Nenner durch den 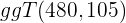
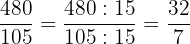
Mit KI zusammenfassen:













