Kapitel

Das bestimmte Integral
Gegeben ist eine Funktion  und ein Intervall
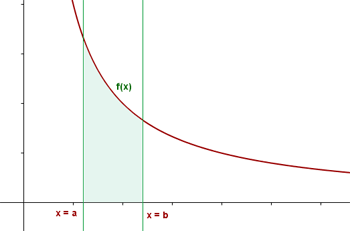
und ein Intervall  . Das bestimmte Integral ist die abgegrenzte Fläche zwischen dem Graphen der Funktion
. Das bestimmte Integral ist die abgegrenzte Fläche zwischen dem Graphen der Funktion  , der x-Achse und den vertikalen Geraden
, der x-Achse und den vertikalen Geraden  und
und 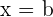 .
.
- Die Schreibweise des bestimmten Integrals ist
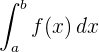 .
.  ist das Zeichen für das Integral.
ist das Zeichen für das Integral.- a ist die untere Integrationsgrenze.
- b ist die obere Integrationsgrenze.
 ist der Integrand oder die zu integrierende Funktion.
ist der Integrand oder die zu integrierende Funktion. ist das Differential von
ist das Differential von  und gibt an, welche Variable der Funktion integriert wird.
und gibt an, welche Variable der Funktion integriert wird.
Eigenschaften des bestimmten Integrals
1 Der Wert des bestimmten Integrals wechselt das Vorzeichen, wenn die Integrationsgrenzen vertauscht werden.
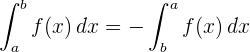
2 Wenn die Integrationsgrenzen übereinstimmen, ist das bestimmte Integral null.

3 Wenn  ein Punkt innerhalb des Intervalls
ein Punkt innerhalb des Intervalls  ist, setzt sich das bestimmte Intervall aus einer Summe von zwei Integralen, die um die Intervalle
ist, setzt sich das bestimmte Intervall aus einer Summe von zwei Integralen, die um die Intervalle  und
und 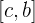 erweitert wurden, zusammen.
erweitert wurden, zusammen.
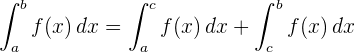
4 Das bestimmte Integral einer Summe von Funktionen ist gleich der Summe der Integrale
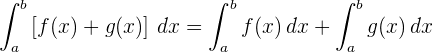
5 Das Integral des Produkts aus einer Konstanten und einer Funktion ist gleich der Konstanten mal dem Integral der Funktion.
Hauptsatz der Differential- und Integralrechnung – 1.
Der Hauptsatz besagt: Das bestimmte Integral einer stetigen Funktion  in einem geschlossenen Intervall
in einem geschlossenen Intervall  ist gleich der Differenz zwischen den Werten, die eine Stammfunktion
ist gleich der Differenz zwischen den Werten, die eine Stammfunktion 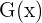 von
von  an den Grenzen des Intevalls einnimmt
an den Grenzen des Intevalls einnimmt
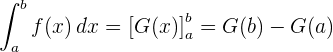
Hauptsatz der Differential- und Integralrechnung – 2.
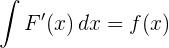
Der Hauptsatz besagt auch, dass die Ableitung und die Integration inverse Rechenoperationen sind.
Wenn eine stetige Funktion integriert und später abgeleitet wird, erhält man die eigentliche Funktion.
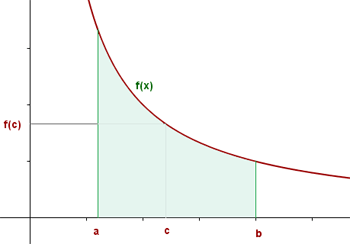
Mittelwertsatz der Integralrechnung
Wenn eine Funktion in einem Intervall  stetig ist, gibt es einen Punkt
stetig ist, gibt es einen Punkt  innerhalb des Intervalls, für den gilt:
innerhalb des Intervalls, für den gilt:
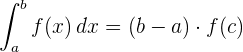
Integralfunktion
Es sei 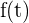 eine stetige Funktion im Intervall
eine stetige Funktion im Intervall  .
.
Von dieser Funktion ausgehend wird die Integralfunktion definiert:
 ,
,
die von der unteren Integrationsgrenze abhängt:
Um Verwechslungen zu vermeiden, gilt, dass wenn auf die Variable von  verwiesen wird, sie
verwiesen wird, sie  genannt wird. Wenn allerdings auf die Variable von
genannt wird. Wenn allerdings auf die Variable von  verwiesen wird, wird sie
verwiesen wird, wird sie  genannt.
genannt.
Grafisch dargestellt stellt die Integralfunktion  den durch den Graphen
den durch den Graphen  , die x-Achse und die Geraden
, die x-Achse und die Geraden 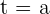 und
und 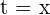 begrenzten Bereich dar.
begrenzten Bereich dar.
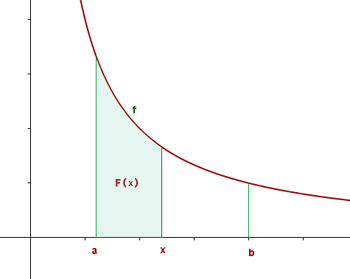
Die Integralfunktion  wird auch Flächeninhaltsfunktion von
wird auch Flächeninhaltsfunktion von  im Intervall
im Intervall  genannt.
genannt.
Mit KI zusammenfassen:













