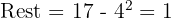Die Quadratwurzel einer ganzen Zahl
Die Quadratwurzel einer positiven ganzen Zahl ist der positive Wert, der quadriert dieser Zahl entspricht.
Beispiel:
Der Radikand ist immer eine positive Zahl oder gleich 0, da jede quadrierte Zahl positiv ist.
Beispiel:
Das Radizieren ist der umgekehrte Vorgang zur Potenzierung. Sie besteht darin, dass man aus zwei Zahlen, dem Radikanden und dem Wurzelexponenten, eine dritte Zahl, die Wurzel, ermittelt, die, mit dem Wurzelexponenten potenziert, dem Radikanden entspricht.
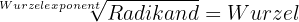
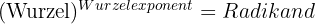
Bei der Quadratwurzel ist der Wurzelexponent 2, obwohl er in diesem Fall weggelassen wird.
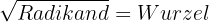
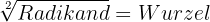
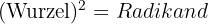
Exakte Quadratwurzel
Die Quadratwurzel einer Zahl "a" ist exakt, wenn wir eine Zahl "b" finden, die quadriert dem Radikanden entspricht::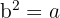 
.
Beispiel:
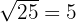
Bei der exakten Quadratwurzel bleibt kein Rest.
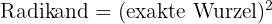
Beispiel:
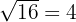
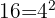
Weitere Beispiele:
Quadratzahlen:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, ...
Ganzzahlige Quadratwurzel
Die Quadratwurzel ist ganzzahlig, sofern der Radikand keine perfekte Quadratzahl ist. Ist eine Zahl keine perfekte Quadratzahl, ist ihre Wurzel ganzzahlig.
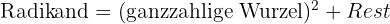
Beispiel:
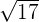
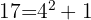
Die ganzzahlige Wurzel einer ganzen Zahl ist die größte ganze Zahl, deren Quadrat kleiner als diese Zahl ist.
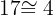Wurzel
Der Rest ist die Differenz zwischen dem Radikanden und dem Quadrat der ganzzahligen Wurzel.
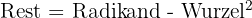
Beispiel:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
