Kapitel
- Nur der Dividend ist eine Dezimalzahl
- Nur der Divisor ist eine Dezimalzahl
- Der Dividend und der Divisor sind Dezimalzahlen
- Division durch eine Einheit, gefolgt von Nullen
- Quadratwurzel aus Dezimalzahlen
- Umwandlung von exakten Dezimalzahlen in Brüche
- Umwandlung einer reinperiodischen Zahl in einen Bruch
- Umwandlung einer gemischtperiodischen Zahl in einen Bruch
- Runden
Nur der Dividend ist eine Dezimalzahl
Die Division von Dezimalzahlen erfolgt so, als wären es ganze Zahlen. Die Division von Dezimalzahlen erfolgt so, als wären es ganze Zahlen. Wenn wir die erste Dezimalzahl nach unten ziehen, setzen wir ein Komma in den Quotienten und dividieren weiter.
Beispiel
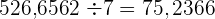
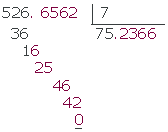
Nur der Divisor ist eine Dezimalzahl
Wir streichen das Komma aus dem Divisor und fügen dem Dividenden so viele Nullen hinzu, wie der Divisor Nachkommastellen hat. Dann dividieren wir, als ob es ganze Zahlen wären.
Beispiel
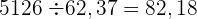
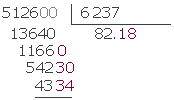
Der Dividend und der Divisor sind Dezimalzahlen
Die Anzahl der Nachkommastellen des Dividenden und des Divisors wird angeglichen, indem so viele Nullen wie Nachkommastellen der Differenz zu derjenigen mit weniger Nachkommastellen hinzugefügt werden. Das Komma fällt dann weg und wir dividieren, als wären es ganze Zahlen.
Beispiel
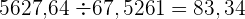
Division durch eine Einheit, gefolgt von Nullen
Um eine Zahl durch die Einheit gefolgt von Nullen zu dividieren, wird das Komma um die Anzahl der Nullen nach der Einheit nach links verschoben.
Beispiel
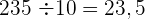
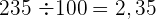
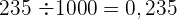
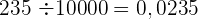
Quadratwurzel aus Dezimalzahlen
Um die Quadratwurzel aus einer Dezimalzahl zu ziehen, müssen wir die folgenden Schritte befolgen:
1 Zweistellige Zahlengruppen werden durch das Komma voneinander getrennt, und zwar nach links (ganzzahliger Teil) und nach rechts (dezimaler Teil).
2 Wenn der Radikand eine ungerade Anzahl von Ziffern in seinem Dezimalteil hat, wird rechts eine Null hinzugefügt.
3 Ohne Berücksichtigung des Kommas wird die Quadratwurzel der resultierenden Zahl gezogen.
4 In die Wurzel werden, von rechts beginnend, so viele Nachkommastellen eingesetzt, wie es Nachkommastellenpaare im Radikanden gibt. Im Rest werden, ebenfalls von rechts beginnend, so viele Dezimalstellen abgetrennt, wie der Radikand enthält.
Beispiel
Umwandlung von exakten Dezimalzahlen in Brüche
Wenn der Bruch eine exakte Dezimalzahl ist, ist der Zähler des Bruchs die angegebene Zahl ohne Komma und der Nenner die Einheit, gefolgt von so vielen Nullen, wie es Nachkommastellen gibt.
Beispiel
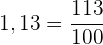
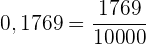
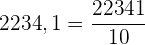
Umwandlung einer reinperiodischen Zahl in einen Bruch
Ist die Zahl reinperiodisch, hat der Bruch als Zähler die angegebene Zahl ohne Komma, abzüglich des ganzzahligen Teils, und als Nenner eine Zahl, die aus so vielen Neunen gebildet wird, wie Ziffern in der Periode vorhanden sind.
Beispiel
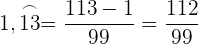
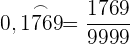
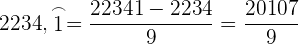
Umwandlung einer gemischtperiodischen Zahl in einen Bruch
Handelt es sich um eine gemischtperiodische Zahl, so hat der Bruch als Zähler die angegebene Zahl ohne Komma, abzüglich des ganzzahligen Teils, gefolgt von den nichtperiodischen Dezimalziffern, und als Nenner eine Zahl, die aus so vielen Neunen gebildet wird, wie Ziffern in der Periode vorhanden sind, gefolgt von so vielen Nullen, wie Ziffern im nichtperiodischen Dezimalteil vorhanden sind.
Beispiel
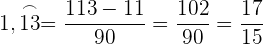
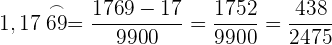
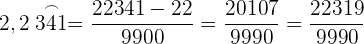
Runden
Um Dezimalzahlen zu runden, müssen wir uns die Dezimaleinheit nach der zu rundenden Einheit ansehen. Wenn die Dezimaleinheit größer oder gleich 
ist, wird die vorherige Dezimaleinheit um eins erhöht; andernfalls wird sie unverändert gelassen.
Beispiel
1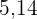 
: Da 
kleiner als ist, wird auf 
gerundet.
2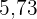 
: Da 
größer als ist, wird auf 
gerundet.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
