Kapitel

Charakteristische Intervalle
Das charakteristische Intervall mit Konfidenzniveau  für eine Normalverteilung
für eine Normalverteilung 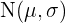 ist gegeben durch
ist gegeben durch
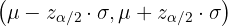
Dabei ist das Konfidenzniveau  die Wahrscheinlichkeit, dass eine der Normalverteilung folgende Zahl in das Intervall fällt.
die Wahrscheinlichkeit, dass eine der Normalverteilung folgende Zahl in das Intervall fällt.
Das Signifikanzniveau wird mit  angegeben. Der Mittelwert der Verteilung ist
angegeben. Der Mittelwert der Verteilung ist  und die Standardabweichung ist
und die Standardabweichung ist  . Der kritische Wert des Intervalls wird mit
. Der kritische Wert des Intervalls wird mit  angegeben.
angegeben.
In der folgenden Tabelle sind einige der häufigsten charakteristischen Intervalle zusammengefasst:
 | 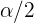 |  | charakteristische Intervalle |
|---|---|---|---|
| 0,90 | 0,05 | 1,645 | 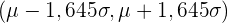 |
| 0,95 | 0,025 | 1,96 | 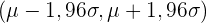 |
| 0,99 | 0,005 | 2,575 | 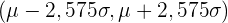 |
Zentraler Grenzwertsatz
Wir betrachten eine Grundgesamtheit  mit Mittelwert
mit Mittelwert  , Standardabweichung
, Standardabweichung  und Stichprobenumfang
und Stichprobenumfang  . Dann folgt der Mittelwert
. Dann folgt der Mittelwert  einer annähernden Normalverteilung. Das heißt,
einer annähernden Normalverteilung. Das heißt,
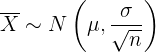
Der Stichprobenumfang muss 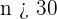 sein. Wenn die ursprüngliche Grundgesamtheit
sein. Wenn die ursprüngliche Grundgesamtheit  einer Normalverteilung folgt, kann
einer Normalverteilung folgt, kann  einen beliebigen Wert haben.
einen beliebigen Wert haben.
Schätzung von Mittelwerten und Verhältnissen
Schätzung des Mittelwerts einer Grundgesamtheit
Wir schätzen mittels Konfidenzintervallen. Für den Mittelwert beträgt das Konfidenzintervall mit Signifikanz 
 ,
,
wobei  der Mittelwert der Stichprobe,
der Mittelwert der Stichprobe,  die Standardabweichung der Grundgesamtheit,
die Standardabweichung der Grundgesamtheit,  der Umfang der Stichprobe und
der Umfang der Stichprobe und  der kritische Wert der Standardnormalverteilung ist.
der kritische Wert der Standardnormalverteilung ist.
In diesem Fall ist der Schätzungsfehler
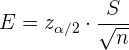
Wenn wir außerdem bereits die Signifikanz  , die Standardabweichung
, die Standardabweichung  und den gewünschten Fehler
und den gewünschten Fehler  kennen, wird der Stichprobenumfang wie folgt berechnet
kennen, wird der Stichprobenumfang wie folgt berechnet

Schätzung einer Proportion
Im Falle der Proportion ist das Konfidenzintervall mit Signifikanz 
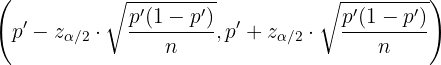 ,
,
wobei  die Proportion der Stichprobe,
die Proportion der Stichprobe,  der kritische Werte der Normalverteilung und
der kritische Werte der Normalverteilung und  der Stichprobenumfang ist.
der Stichprobenumfang ist.
Hier beträgt der maximale Schätzfehler
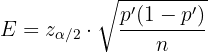
Bei Proportionen ist es üblich, 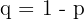 zu schreiben, wobei
zu schreiben, wobei  die Erfolgswahrscheinlichkeit und
die Erfolgswahrscheinlichkeit und 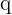 die Fehlerwahrscheinlichkeit (eines Individuums in der Grundgesamtheit mit einer bestimmten Eigenschaft) ist.
die Fehlerwahrscheinlichkeit (eines Individuums in der Grundgesamtheit mit einer bestimmten Eigenschaft) ist.
Schätzung der Standardabweichung
Im Falle der Standardabweichung  wird das Konfidenzintervall der Varianz
wird das Konfidenzintervall der Varianz 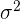 berechnet, das wie folgt gegeben ist
berechnet, das wie folgt gegeben ist
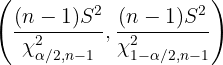 ,
,
wobei  der Stichprobenumfang,
der Stichprobenumfang, 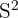 die Varianz der Stichprobe ist und wie folgt berechnet wird
die Varianz der Stichprobe ist und wie folgt berechnet wird
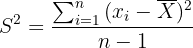 ,
,
wobei  der Mittelwert der Stichprobe ist.
der Mittelwert der Stichprobe ist. 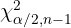 und
und 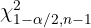 sind die kritischen Werte einer Verteilung
sind die kritischen Werte einer Verteilung 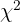 ; diese Werte werden von einem Computerprogramm berechnet oder aus einer Chi-Tabelle entnommen.
; diese Werte werden von einem Computerprogramm berechnet oder aus einer Chi-Tabelle entnommen.
Hypothesentests
Das Verfahren zur Durchführung eines Hypothesentests für den Parameter  einer Grundgesamtheit ist wie folgt:
einer Grundgesamtheit ist wie folgt:
1 Die Nullhypothese  und die Alternativhypothese
und die Alternativhypothese  werden angegeben. Bei der Nullhypothese wird eine Annahme über den Wert von
werden angegeben. Bei der Nullhypothese wird eine Annahme über den Wert von  getroffen und
getroffen und  ist die gegenteilige Annahme. Die folgende Tabelle gibt einen Überblick über die möglichen Hypothesentests:
ist die gegenteilige Annahme. Die folgende Tabelle gibt einen Überblick über die möglichen Hypothesentests:
| einseitig |  |  |
| zweiseitig | 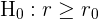 |  H_A: r < r_0[/latex] H_A: r < r_0[/latex] |
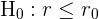 | 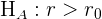 |
2 Berechne das Signifikanzniveau  und ermittle daraus die kritischen Werte
und ermittle daraus die kritischen Werte  (für den zweiseitigen Fall) oder
(für den zweiseitigen Fall) oder 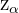 (für den einseitigen Fall).
(für den einseitigen Fall).
3 Bestimme den Akzeptanzbereich des Stichprobenparameters.
4 Berechne den Wert des Stichprobenparameters 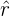 .
.
5 Ziehe die Schlussfolgerung. Wenn der Wert des Stichprobenparameters innerhalb des Akzeptanzbereichs liegt, dann akzeptieren wir die Nullhypothese mit einem Signifikanzniveau von  . Andernfalls lehnen wir die Nullhypothese ab.
. Andernfalls lehnen wir die Nullhypothese ab.
Zweiseitiger Test
Wenn wir einen zweiseitigen Test haben und eine Hypothese für den Mittelwert  der Grundgesamtheit testen:
der Grundgesamtheit testen:

Somit lautet der Akzeptanzbereich
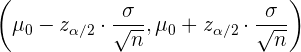
Handelt es sich hingegen um einen Hypothesentest für die Proportion  ,
,

der Akzeptanzbereich ist also
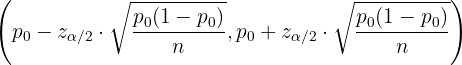 ,
,
wobei  die Standardabweichung der Grundgesamtheit,
die Standardabweichung der Grundgesamtheit,  der Stichprobenumfang und
der Stichprobenumfang und  der kritische Wert der Verteilung ist.
der kritische Wert der Verteilung ist.
Einseitiger Test größer oder gleich
Bei einem einseitigen Test des Typs „größer oder gleich“ wird eine Hypothese für den Mittelwert  der Grundgesamtheit getestet, das heißt,
der Grundgesamtheit getestet, das heißt,

Der Akzeptanzbereich ist also

Handelt es sich hingegen um einen Hypothesentest für die Proportion  ,
,

Somit ist der Akzeptanzbereich
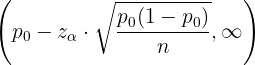 ,
,
wobei  die Standardabweichung der Grundgesamtheit,
die Standardabweichung der Grundgesamtheit,  der Stichprobenumfang und
der Stichprobenumfang und 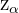 der kritische Wert der Verteilung ist.
der kritische Wert der Verteilung ist.
Einseitiger Test kleiner oder gleich
Bei einem einseitigen Test des Typs „kleiner oder gleich“ wird eine Hypothese für den Mittelwert  der Grundgesamtheit getestet, das heißt,
der Grundgesamtheit getestet, das heißt,

Somit ist der Akzeptanzbereich
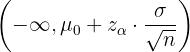
Handelt es sich hingegen um einen Hypothesentest für die Proportion  ,
,

Somit ist der Akzeptanzbereich
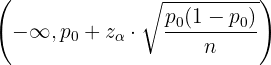 ,
,
wobei wieder  die Standardabweichung der Grundgesamtheit,
die Standardabweichung der Grundgesamtheit,  der Stichprobenumfang und
der Stichprobenumfang und 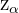 der kritische Wert der Verteilung ist.
der kritische Wert der Verteilung ist.
In der folgenden Tabelle sind die kritischen Werte 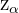 für verschiedene Werte von
für verschiedene Werte von  zusammengefasst, die für die einseitigen Tests verwendet werden:
zusammengefasst, die für die einseitigen Tests verwendet werden:
 |  | 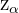 |
|---|---|---|
| 0,90 | 0,10 | 1,28 |
| 0,95 | 0,05 | 1,645 |
| 0,99 | 0,01 | 2,33 |
Fehler
Es gibt zwei Arten von Fehlern: Fehler vom Typ 1, der auftritt, wenn wir die Nullhypothese ablehnen, obwohl sie wahr ist, und Fehler vom Typ 2, der auftritt, wenn wir die Nullhypothese annehmen, obwohl sie falsch ist.
In der folgenden Tabelle sind die Fehlertypen zusammengefasst:
 | richtig | falsch |
|---|---|---|
| Annehmen | richtige Entscheidung Wahrscheinlichkeit von  | falsche Entscheidung: Fehler Typ 2 |
| Ablehnen | falsche Entscheidung Fehler Typ 1 Wahrscheinlichkeit von  | richtige Entscheidung |
Mit KI zusammenfassen:












