Ordne die folgenden ganzen Zahlen in aufsteigender Reihenfolge, stelle sie grafisch dar und berechne ihre Gegenzahlen und Absolutbeträge:
8, −6, −5, 3, −2, 4, −4, 0, 7
Ordne die folgenden ganzen Zahlen in aufsteigender Reihenfolge, stelle sie grafisch dar und berechne ihre Gegenzahlen und Absolutbeträge:
8, −6, −5, 3, − 2, 4, −4, 0, 7
Lösung:
− 6 < − 5 < − 4 < − 2 < 0 < 3 < 4 < 7 < 8

Berechnung der Gegenzahl und des Absolutbetrags:
1 (−6) = −(−6) = 6 |−6| = 6
2 (−5) = −(−5) = 5 |−5| = 5
3 (−4) = −(−4) = 4 |−4| = 4
4 (−2) = −(−2) = 2 |−2| = 2
5 (0) = |0| = 0
6 (3) = −3 |3| = 3
7 (4) = −4 |4| = 4
8 (7) = −7 |7| = 7
9 (8) = −8 |8| = 8
Stelle die folgenden ganzen Zahlen grafisch dar und berechne ihre Gegenzahlen sowie ihre Absolutbeträge:
−4, 6, −2, 1, −5, 0, 9
Stelle die folgenden ganzen Zahlen grafisch dar und berechne ihre Gegenzahlen sowie ihre Absolutwerte:
−4, 6, −2, 1, −5, 0, 9
Lösung:

Berechnung der Gegenzahl und des Absolutbetrags:
1 (−4) = −(−4) = 4 |−4| = 4
2 (6) = −6 |6| = 6
3 (−2) = −(−2) = 2 |−2| = 2
4 (1) = −1 |1| = 1
5 (−5) = −(−5) = 5 |−5| = 5
6 (0) = |0| = 0
7 (9) = −9 |9| = 9
Absolutbetrag und Gegenzahl
Stelle die folgenden ganzen Zahlen grafisch dar und berechne ihre Gegenzahlen sowie ihre Absolutbeträge:
−4, 6, −2, 1, −5, 0, 9
Stelle die folgenden ganzen Zahlen grafisch dar und berechne ihre Gegenzahlen sowie ihre Absolutwerte:
−4, 6, −2, 1, −5, 0, 9
Lösung:

Berechnung der Gegenzahl und des Absolutbetrags:
1 (−4) = −(−4) = 4 |−4| = 4
2 (6) = −6 |6| = 6
3 (−2) = −(−2) = 2 |−2| = 2
4 (1) = −1 |1| = 1
5 (−5) = −(−5) = 5 |−5| = 5
6 (0) = |0| = 0
7 (9) = −9 |9| = 9
Faktorisieren
Gemeinsamen Faktor ausklammern:
1 3 · 2 + 3 · (−5) =
2 (−2) · 12 + (−2) · (−6) =
3 8 · 5 + 8 =
4 (−3) · (−2) + (−3) · (−5) =
Gemeinsamen Faktor ausklammern:
Hinweis: Bei diesen Aufgaben wenden wir das an: a (b+c)= a·b + a·c
1 Direkte Lösung: 3 · 2 + 3 · (−5) = 6 + (-15)= 6 - 15 = - 9
Faktorisieren: Wir stellen fest, dass der gemeinsame Faktor 3 ist. Wir klammern ihn mit dem Distributivgesetz aus
3( 2 + (-5) )
Probe :
3(2+(-5)) = 3(2-5)=3(-3)= 9
2 (−2) · 12 + (−2) · (−6) = - 24 + 12 = -12
Faktorisieren: Wir stellen fest, dass der gemeinsame Faktor -2 ist. Wir klammern ihn mit dem Distributivgesetz aus
-2( 12 + (-6) )
Probe:
-2( 12 + (-6) ) = -2( 12-6)= -2(6)=-12
3 8 · 5 + 8 = 40 + 8 = 48
Faktorisieren : Wir stellen fest, dass der gemeinsame Faktor 8 ist. Wir klammern ihn mit dem Distributivgesetz aus
8( 5+1 )
Probe:
8( 5+1 ) =8(6)=48
4 (−3) · (−2) + (−3) · (−5) = 6 + 15 = 21
Faktorisieren: Wir stellen fest, dass der gemeinsame Faktor -3 ist. Wir klammern ihn mit dem Distributivgesetz aus
-3( (-2)+(-5) )
Probe :
-3( (-2)+(-5) ) = -3(-2-5)= -3(-7)=21
Führe folgende Rechenoperationen mit ganzen Zahlen aus:
1 (3 − 8) + [5 − (−2)]
2 5 − [6 − 2 − (1 − 8) −3 + 6] + 5
3 9 : [6 : (− 2)]
4 [(−2)5 − (−3)³]²
5 (5 + 3 · 2 : 6 − 4 ) · (4 : 2 − 3 + 6) : (7 − 8 : 2 − 2)²
6 [(17 − 15)³ + (7 − 12)²] : [(6 − 7) · (12 − 23)]
Führe folgende Rechenoperationen mit ganzen Zahlen aus:
Lösungen:
1 (3 − 8) + [5 − (−2)] =
Wir schreiben die Gegenzahl von (−2)
= −5 + (5 + 2) =
Wir addieren innerhalb der Klammer
= −5 + 7 = 2
2 5 − [6 − 2 − (1 − 8) − 3 + 6] + 5 =
Wir führen die Berechnungen in der Klammer durch
= 5 − [6 − 2 − (−7) − 3 + 6] + 5 =
Wir berechnen die Gegenzahl von (−7)
= 5 − (6 − 2 + 7 − 3 + 6) + 5 =
Wir führen die Berechnungen in der Klammer durch und nehmen die Gegenzahl des Ergebnisses
= 5 − 14 + 5 = −4
3 9 : [6 : (−2)] =
Wir dividieren innerhalb der eckigen Klammer
= 9 : (−3) = −3
4 [(−2)5 − (−3)³]² =
Wir berechnen die Potenzen in der Klammer. Bei (−2)5 gehen wir wie folgt vor: (-2)(-2) = 4. 4(-2) = -8. -8 (-2) = 16. 16 (-2) = -32. Bei (−3)³ gehen wir genauso vor und erhalten (-3)(-3) = 9. 9 (-3) = -27
= [−32 − (−27)]² =
Wir eliminieren die eckige Klammer
= (−32 + 27)² =
Wir berechnen und quadrieren
= (−5)² = 25
5 (5 + 3 · 2 : 6 − 4 ) · (4 : 2 − 3 + 6) : (7 − 8 : 2 − 2)² =
Wir rechnen 3 · 2 (Multiplikation) und dividieren
= (5 + 6 : 6 − 4 ) · (2 − 3 + 6) : (7 − 4 − 2)² =
Wir führen die Division durch
= (5 + 1 − 4 ) · (2 − 3 + 6) : (7 − 4 − 2)² =
Wir rechnen die Klammern aus
= 2 · 5 : 1² =
Wir quadrieren
= 2 · 5 : 1 =
Zuerst müssen wir multiplizieren und dann dividieren
= 10 : 1 =10
6 [(17 − 15)³ + (7 − 12)²] : [(6 − 7) · (12 − 23)]
Wir führen die Berechnungen innerhalb der Klammern aus
= [(2)³ + (−5)²] : [(−1) · (−11)]
Wir berechnen die Potenzen
= (8 + 25) : [(−1) · (−11)] =
Wir führen die Rechenoperationen in der runden und eckigen Klammer durch und dividieren die Ergebnisse
= 33 : 11 = 3
Führe folgende Rechenoperationen mit ganzen Zahlen durch:
1 (7 − 2 + 4) − (2 − 5)
2 1 − (5 − 3 + 2) − [5 − (6 − 3 + 1) − 2]
3 −12 · 3 + 18 : (−12 : 6 + 8)
4 2 · [( −12 + 36) : 6 + (8 − 5) : (−3)] - 6
5 [(−2)5 · (−3)2] : (−2)2 = (−32 · 9) : 4
6 6 + {4 − [(17 − (4 · 4)] + 3} − 5
Führe folgende Rechenoperationen mit ganzen Zahlen durch:
Lösungen:
1 (7 − 2 + 4) − (2 − 5) =
Wir rechnen die Klammern aus
= 9 − (−3) =
Wir nehmen die Gegenzahl von (−3)
= + 3 = 12
2 1 − (5 − 3 + 2) − [5 − (6 − 3 + 1) − 2] =
Wir rechnen die runden Klammern aus
= 1 − (4) − [5 − (4) − 2] =
Wir nehmen die Gegenzahl der beiden Zahlen 4
= 1 − 4 − (5 − 4 − 2) =
Wir rechnen die Klammer aus
= 1 − 4 − 5 + 4 + 2 =
Und erhalten
= 1 − 5 + 2 = −2
3 −12 · 3 + 18 : (−12 : 6 + 8) =
Wir dividieren innerhalb der Klammer
= − 12 · 3 + 18 : (−2 + 8) =
Und lösen die Klammer schließlich auf
= −12 · 3 + 18 : 6 =
Wir multiplizieren und dividieren
= −36 + 3 = −33
4 2 · [( −12 + 36) : 6 + (8 − 5) : (−3)] − 6 =
Wir führen die Rechenoperationen in den ersten beiden runden Klammern durch
= 2 · [24 : 6 + 3 : (−3)] − 6 =
Wir dividieren
= 2 · [ 4 + (−1)] − 6 =
Wir lösen die eckige Klammer auf
= 2 · 3 − 6 =
Nun multiplizieren wir
= 6 − 6 = 0
5 [(−2)5 · (−3)²] : (−2)² =
Wir berechnen die Potenzen
= (−32 · 9) : 4 =
Und lösen die runde Klammer auf
= −288 : 4 = −72
6 6 + {4 − [(17 − (4 · 4)] + 3} − 5 =
Wir multiplizieren
= 6 + [4 − (17 − 16) + 3] − 5 =
Wir lösen die runde Klammer auf; aus der eckigen Klammer wird nun eine runde Klammer
= 6 + (4 − 1 + 3) − 5 =
Wir führen die Rechenoperationen in der Klammer durch
= 6 + 6 − 5 = 7
Berechne das Ergebnis der Potenz und prüfe dann, ob das Ergebnis eine in den reellen Zahlen vorhandene Quadratwurzel hat:
1 (−9)²
2 (−1)7
3 (−3)² · (−3)
4 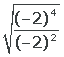
5 (−2)³
6 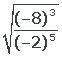
Berechne das Ergebnis der Potenz und prüfe dann, ob das Ergebnis eine in den reellen Zahlen vorhandene Quadratwurzel hat:
Lösungen:
1 (−9)² = 81
Die Quadratwurzel von 81 ist ± 9
2 (−1)7 = −1
Die Quadratwurzel von -1 existiert nicht in den reellen Zahlen, daher hat diese Wurzel keine Lösung in der Menge der reellen Zahlen
Im Allgemeinen gibt es keine Quadratwurzel aus einer negativen Zahl, da es keine Zahl zum Quadrat mit negativem Vorzeichen gibt
3 (−3)² · (−3) =
Wir berechnen das Produkt der Potenzen und nehmen den Ausdruck hoch 3
= (−3)³ = −27
Die Quadratwurzel von -27 hat keine Lösung
4 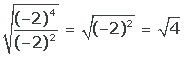
Wir dividieren die Potenzen, quadrieren und ziehen die Wurzel
Das Ergebnis ist 2. Die Quadratwurzel von 2 existiert in den reellen Zahlen.
5 (−2)³ = −8
Die Quadratwurzel von -8 hat keine reelle Lösung
6 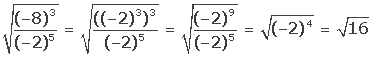
Wir schreiben die Zahl 8 in Form einer Potenz, berechnen die Potenz einer Potenz im Zähler, dividieren die Potenzen, nehmen hoch 4 und ziehen die Wurzel
Das Ergebnis ist 4 und die Quadratwurzel von 4 ist ±2.
Führe folgende Rechenoperationen mit Potenzen ganzer Zahlen durch:
1 (−2)² · (−2)³ · (−2)4
2 (−8) · (−2)² · (−2)0 (−2)
3 (−2)−2 · (−2)³ · (−2)4
4 2−2 · 2−3 · 24
5 2² : 2³
6 2-2 : 2³
7 2² : 2-3
8 2-2 : 2-3
9 [(−2)− 2] 3 · (−2)³ · (−2)4
10 [(−2)6 : (−2)³]³ · (−2) · (−2)−4
Führe folgende Rechenoperationen mit Potenzen ganzer Zahlen durch:
Lösungen:
Hinweis: Um diese Aufgaben zu lösen, wenden wir die Potenzgesetze an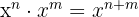
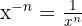

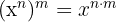
1 (−2)² · (−2)³ · (−2)4 = (−2)9 = −512
Das Ergebnis hat dann ein negatives Vorzeichen, weil die Basis negativ und der Exponent ungerade ist.
2 (−8) · (−2)² · (−2)0 (−2) =
Zunächst zerlegen wir die 8 in Faktoren
(−2)³ · (−2)² · (−2)0 · (−2) = (−2)6 = 64
Das Ergebnis hat ein positives Vorzeichen, da die Basis negativ und der Exponent gerade ist.
3 (−2)−2 · (−2)³ · (−2)4 = (−2)5 = −32
4 2−2 · 2−3 · 24 = 2−1 = 1/2
Da der Exponent negativ ist, müssen wir den Kehrwert der Basis nehmen, d. h. das entsprechende Vorzeichengesetz anwenden
5 5 2² : 2³ = 2−1 = 1/2
Da der Exponent negativ ist, müssen wir den Kehrwert der Basis nehmen, d. h. das entsprechende Vorzeichengesetz anwenden
6 2−2 : 2³ = 2−5 = 1/25 = 1/32
7 2² : 2−3 = 25 = 32
8 2−2 : 2−3 = 2
9 [(−2)−2]³ · (−2)³ · (−2)4 = (−2)−6 · (−2)7 = −2
10 [(−2)6 : (−2)³] 3 · (−2)· (−2)−4 = [(−2)³]³ · (−2)−3 = (−2)9 · (−2)−3= (−2)6 = 64
Führe die folgenden Rechenoperationen mit Potenzen von ganzen Zahlen durch:
1 (−3)1 · (−3)³ · (−3)4 =
2 (−27) · (−3) · (−3)² · (−3)0=
3 (−3)² · (−3)³ · (−3)−4 =
4 3−2 · 3−4 · 34 =
5 5² : 5³ =
6 5-2 : 5³ =
7 5² : 5-3 =
8 5-2 : 5-3 =
9 (−3)1 · [(−3)³]² · (−3)−4 =
10 [(−3)6 : (−3)³]³ · (−3)0 · (−3)−4 =
Führe die folgenden Rechenoperationen mit Potenzen durch:
Lösungen:
1 1 (−3)1 · (−3)³ · (−3)4 = (−3)8 = 6561
2 (−27) · (−3) · (−3)² · (−3)0= (−3)³ · (−3) · (−3)² · (−3)0 = (−3)6 = 729
3 (−3)² · (−3)³ · (−3)−4 = −3
4 3−2 · 3−4 · 34 = 3−2 = 1/3² = 1/9
5 5² : 5³ = 5−1 = 1/5
6 5−2 : 5³ = 5−5 = 1/55 = 1/3125
7 5² : 5−3 = 55 = 3125
8 5−2 : 5−3 = 5
9 (−3)1 · [(−3)³]² · (−3)−4 = (−3)1 · (−3)6· (−3)−4 = (−3)³
Wir berechnen zunächst die Potenz einer Potenz und multiplizieren dann
10 [(−3)6 : (−3)³]³ · (−3)0 · (−3)−4 = [(−3)³]³ · (−3)0· (−3)−4 = (−3)9 · (−3)0 · (−3)−4 = (−3)5 =−243
Zuerst führen wir die in der eckigen Klammer angegebene Division durch, dann die Potenz einer Potenz und schließlich multiplizieren wir die Potenzen
Mit KI zusammenfassen:


