Kapitel
Der größte gemeinsame Teiler (ggT) von zwei oder mehr Zahlen ist die größte Zahl, durch die dividiert werden kann.
Die Zahl 4 ist der größte gemeinsame Teiler von 16 und 20, da sie die größte Zahl ist, durch die die beiden Zahlen dividiert werden kann.
Berechnung des größten gemeinsamen Teilers
1 Die Zahlen werden in Primfaktoren zerlegt.
2 Es werden die gemeinsamten Faktoren mit dem kleinsten Exponenten genommen.
3 Diese Faktoren werden multipliziert und das Ergebnis ist der ggT.
Beispiel für die Berechnung des größten gemeinsamen Teilers
Berechne den ggT von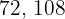 
und 
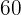
1 Wir zerlegen die Zahlen 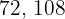und 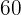in Primfaktoren
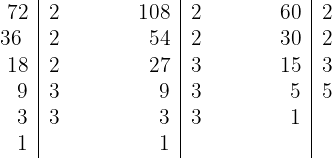
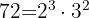
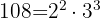
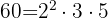
2
und 
sind die gemeinsamen Zahlen. Daher nehmen wir sie hoch den kleinsten Exponenten: 
und
3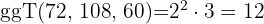 
ist die größte Zahl, durch die 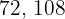und 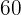dividiert werden können
Eigenschaften des größten gemeinsamen Teilers
1 Die gemeinsamen Teiler mehrerer Zahlen stimmen mit den Teilern des größten gemeinsamen Teilers überein.
Beispiel:
Berechne die gemeinsamen Teiler von 
und 
.
Berechne den ggT
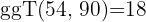
Die gemeinsamen Teiler von und sind Teiler von 
und somit wären sie 
.
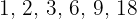2 Wenn mehrere Zahlen mit einer anderen Zahl multipliziert oder durch sie dividiert werden, wird auch ihr größter gemeinsamer Teiler mit derselben Zahl multipliziert oder durch sie dividiert.
Beispiel:
Der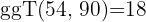
Wenn wir die beiden Zahlen mit multiplizieren, erhalten wir
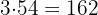
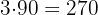
Der ggT von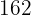 
und 
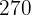ist
Der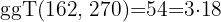 
3 Diese Eigenschaft ergibt sich aus der vorherigen: Gegeben sind mehrere Zahlen. Wenn man sie durch ihren größten gemeinsamen Teiler (ggt) dividiert, sind die resultierenden Quotienten teilerfremd und ihr ggT ist 1..
Beispiel:
Der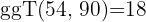
Wenn wir die beiden Zahlen durch dividieren, erhalten wir
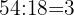
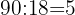
Der ggT von und 
ist 
4 Wenn eine Zahl ein Teiler der anderen Zahl ist, ist dieser der ggT der beiden Zahlen.
Beispiel:
Die Zahl ist ein Teiler von
Wir berechnen den ggT von und
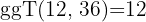
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
