Kapitel
Einseitiger Test
Ein Soziologe hat vorausgesagt, dass in einer bestimmten Stadt die Wahlenthaltung bei den nächsten Wahlen bei mindestens 40 % liegen wird. Eine Zufallsstichprobe von 200 Wahlberechtigten wird nach dem Zufallsprinzip ausgewählt, von denen 75 bereit wären zu wählen. Bestimme mit einem Signifikanzniveau von 1 %, ob die Prognose zulässig ist.
1 Wir geben die Null- und die Alternativhypothese an:H0 : μ ≥ 0,40 Die Stimmenthaltung beträgt mindestens 40 %.
H1 : μ < 0,40 Die Stimmenthaltung beträgt höchstens 40 %;
2 Akzeptanzbereich
α = 0,01 entspricht einem kritischen Wert: zα = 2,33.
Wir bestimmen das Konfidenzintervall für den Mittelwert:
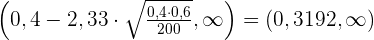
3 Überprüfung
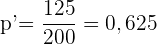
4 Entscheidung
Wir akzeptieren die Nullhypothese H0. Mit einem Signifikanzniveau von 1 % können wir davon ausgehen, dass die Stimmenthaltung mindestens 40 % beträgt.
Aus einem Bericht geht hervor, dass der durchschnittliche Flugpreis zwischen den Kanarischen Inseln und Madrid höchstens 120 € beträgt, mit einer Standardabweichung von 40 €. Bei einer Stichprobe von 100 Reisenden liegt der Durchschnittspreis ihrer Tickets bei 128 €.
Kann die ursprüngliche Aussage mit einem Signifikanzniveau von 0,1 akzeptiert werden?
1 Wir geben die Null- und die Alternativhypothese an:H0 : μ ≤ 120
H1 : μ > 120
2 Akzeptanzbereich
α = 0,1 entspricht einem kritischen Wert: zα = 1,28 .
Wir bestimmen das Konfidenzintervall:
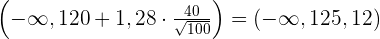
3 Überprüfung
Aus dem Stichprobenmittelwert ermittelter Wert: 128 €.
4 Entscheidung
Wir akzeptieren die Nullhypothese H0 nicht. Bei einem Signifikanzniveau von 10 %.
Ein Nusshersteller gibt an, dass höchstens 6 % der Nüsse leer sind. Es wurden 300 Nüsse nach dem Zufallsprinzip ausgewählt und 21 davon als leer befunden.
a. Kann die Behauptung des Herstellers mit einem Signifikanzniveau von 1 % akzeptiert werden?
b. Wenn der prozentuale Anteil der leeren Nüsse in der Stichprobe beibehalten wird und 1-α = 0,95 ist, welcher Stichprobenumfang wäre dann erforderlich, um den Anteil der Nüsse mit einem Fehler von weniger als 1 % Prozent zu schätzen?
Abschnitt 1
1 Wir geben die Null- und die Alternativhypothese an:
H0 : p ≤ 0,06
H1 : p >0,06
2 Akzeptanzbereich
α = 0,01 entspricht einem kritischen Wert:
zα = 2,33.
Wir bestimmen das Konfidenzintervall:
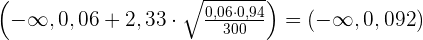
3 Überprüfung
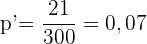
4 Entscheidung
Wir akzeptieren die Nullhypothese H0. Mit einem Signifikanzniveau von 1 %.
Abschnitt 2
1 - α = 0,95 z α/2 = 1, 96
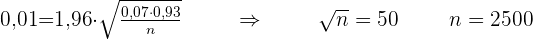
Der Mindeststichprobenumfang beträgt daher n ≥ 2501
Die Lebensdauer der von einem Unternehmen hergestellten 100-W-Glühlampen folgt einer Normalverteilung mit einer Standardabweichung von 120 Stunden Lebensdauer. Ihre durchschnittliche Lebensdauer beträgt garantiert mindestens 800 Stunden. Eine Stichprobe von 50 Glühbirnen wird nach dem Zufallsprinzip aus einer Charge ausgewählt und nach einem Test wird eine durchschnittliche Lebensdauer von 750 Stunden ermittelt. Müsste die Charge bei einem Signifikanzniveau von 0,01 als nicht garantiefähig abgelehnt werden?
1 Wir geben die Null- und die Alternativhypothese an:H0 : µ ≥ 800
H1 : µ <800
2 Akzeptanzbereich:
α = 0,01; zα = 2,33
Wir bestimmen das Konfidenzintervall:
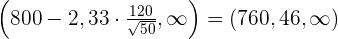
3 Überprüfung
x = 750
4 Entscheidung
Wir lehnen die Nullhypothese H0 ab. Mit einem Signifikanzniveau von 1 %.
Die Qualitätskontrolle einer Akkufabrik hat den Verdacht, dass bei der Produktion eines Akkumodells für Mobiltelefone Fehler aufgetreten sind, die die Lebensdauer des Akkus verkürzen. Bislang folgte die Gesprächszeit einer Normalverteilung mit einem Mittelwert von 300 Minuten und einer Standardabweichung von 30 Minuten. Die Prüfung der letzten produzierten Charge vor der Auslieferung an den Markt ergab jedoch, dass bei einer Stichprobe von 60 Akkus die durchschnittliche Gesprächszeit 290 Minuten betrug. Angenommen, diese Dauer bleibt normal und hat die gleiche Standardabweichung:
Kann man bei einem Signifikanzniveau von 2 % davon ausgehen, dass der Verdacht der Qualitätskontrolle zutrifft?
1 Wir geben die Null- und die Alternativhypothese an:H0 : µ ≥ 300
H1 : µ < 300
2 Akzeptanzbereich
α = 0,02; 1- α = 0,98; P(1,96)= 0,98; zα = 1,96 .
Wir bestimmen das Konfidenzintervall:
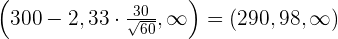
3 Überprüfung
µ = 290
4 Entscheidung
Wir lehnen die Nullhypothese H0 ab. Bei einem Signifikanzniveau von 2 %.
Zweiseitiger Test
Es ist bekannt, dass die Standardabweichung der Punkte in einer bestimmten Mathematikprüfung 2,4 beträgt. Bei einer Stichprobe von 36 Studenten wurde ein Mittelwert von 5,6 ermittelt. Bestätigen diese Daten die Hypothese, dass der Mittelwert der Prüfung bei 6 lag, mit einem Konfidenzniveau von 95 %?
1 Wir geben die Null- und die Alternativhypothese an:H0 : μ = 6 Die durchschnittliche Punktzahl hat sich nicht verändert.
H1 : μ ≠ 6 Die durchschnittliche Punktzahl hat sich geändert.
2 Akzeptanzbereich
α = 0,05 entspricht einem kritischen Wert: zα/2 = 1,96.
Wir bestimmen das Konfidenzintervall für den Mittelwert.
Wir wenden folgende Formel an:
Punktuelle Schätzung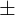 
(kritischer Wert) · (Standardfehler)
Wir kennen die punktuelle Schätzung: 
Wir kennen den kritischen Wert: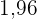 
Wir ermitteln den Standardfehler. Seine Formel lautet: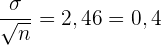 
Wir erhalten
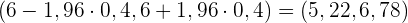
3 Überprüfung
Wert, der sich aus dem Stichprobenmittelwert ergibt: 5,6 .
4 Entscheidung
Wir akzeptieren die Nullhypothese H0 bei einem Signifikanzniveau von 5%.
Ein Hersteller elektrischer Lampen testet ein neues Produktionsverfahren, das als akzeptabel gilt, wenn die nach diesem Verfahren hergestellten Lampen eine normale Grundgesamtheit mit einer durchschnittlichen Lebensdauer von 2400 Stunden und einer Standardabweichung von 300 Stunden ergeben. Eine Stichprobe von 100 Lampen, die nach dieser Methode hergestellt wurden, hat eine durchschnittliche Lebensdauer von 2320 Stunden. Kann die Hypothese der Gültigkeit des neuen Herstellungsverfahrens mit einem Risiko von 5 % oder weniger akzeptiert werden?
1 Wir geben die Null- und die Alternativhypothese an:H0 : μ = 2400
H1 : μ ≠2400
2 Akzeptanzbereich
α = 0,05 entsprich einem kritischen Wert:zα/2 = 1,96.
Wir bestimmen das Konfidenzintervall für den Mittelwert:
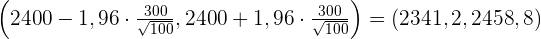
3 Überprüfung
Aus dem Stichprobenmittelwert ermittelter Wert: 2320 .
4 Entscheidung
Wir lehnen die Nullhypothese H0 mit einem Signifikanzniveau von 5 % ab.
Man geht davon aus, dass der mittlere Protombin-Spiegel bei einer normalen Bevölkerung 20 mg/100 ml Plasma mit einer Standardabweichung von 4 Milligramm/100 ml beträgt. Um dies zu prüfen, wird eine Stichprobe von 40 Personen entnommen, bei denen der Mittelwert 18,5 mg/100 ml beträgt. Kann die Hypothese mit einem Signifikanzniveau von 5 % akzeptiert werden?
1 Wir geben die Null- und die Alternativhypothese an:H0 : μ =20 mg/100 ml
H1 : μ ≠ 20 mg/100 ml
2 Akzeptanzbereich
α = 0,05 entspricht einem kritischen Wert: zα/2 = 1,96.
Wir bestimmen das Konfidenzintervall für den Mittelwert:
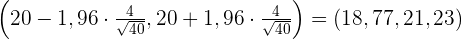
3 Überprüfung
Aus dem Stichprobenmittelwert ermittelter Wert: 18,5.
4 Entscheidung
Wir lehnen die Nullhypothese H0 mit einem Signifikanzniveau von 5 % ab.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
