Stichprobe
In einem bestimmten Viertel soll eine Studie durchgeführt werden, um mehr über die Art der Freizeitaktivitäten zu erfahren, die die Bewohner*innen am liebsten mögen. Zu diesem Zweck werden 100 zufällig ausgewählte Personen befragt.
a Erkläre, welches Auswahlverfahren besser geeignet ist: Stichprobe mit oder ohne Ersatz. Weshalb?
b Da sich die Präferenzen mit dem Alter ändern und bekannt ist, dass in dem Viertel 2.500 Kinder, 7.000 Erwachsene und 500 ältere Menschen leben, wird beschlossen, die oben genannte Stichprobe anhand einer geschichteten Stichprobe mit proportionaler Verteilung auszuwählen. Bestimme den Stichprobenumfang für jede Schicht.
a Da die Grundgesamtheit endlich ist, können wir die Formeln, die wir kennen, für die Stichprobenziehung mit Ersatz verwenden.
Eine Stichprobe ohne Ersatz ist jedoch möglich, mit dem einzigen Nachteil, dass die Berechnungen etwas komplizierter sind.
b 
sei die Grundgesamtheit und 
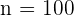der Stichprobenumfang. Wir bezeichnen 
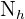als Umfang der Schicht 
und 
als Umfang der Stichprobe, den wir aus nehmen. Bei der geschichteten Zufallsstichprobe mit proportionaler Schichtung gilt, dass
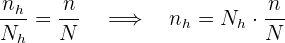
Deshalb müssen wir die Werte für jede Schicht ermitteln. Die Umfänge der einzelnen Schichten sind: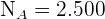 
(Kinder), 
(Erwachsene) und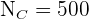 
(Senior*innen).
Der Stichprobenumfang der Kinder ist also:
Der Stichprobenumfang der Erwachsenen ist:
Der Stichprobenumfang der Senior*innen ist:
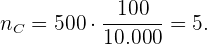
Wir stellen fest, dass die Stichprobenumfänge addiert 100 ergeben:
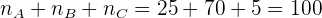
Konfidenzintervalle
In 16 zufällig ausgewählten Geschäften eines Stadtviertels wurden die Preise für ein und dasselbe Lebensmittel stichprobenartig erhoben, wobei sich folgende Preise ergaben:
95, 108, 97, 112, 99, 106, 105, 100, 99, 98, 104, 110, 107, 111, 103, 110.
Unter der Annahme, dass die Preise für dieses Produkt einer Normalverteilung mit Varianz 25 und unbekanntem Mittelwert folgen:
a Wie lautet die Verteilung des Mittelwerts der Stichprobe?
b Bestimme das Konfidenzintervall bei 95 % für den Mittelwert der Grundgesamtheit.
a Wir benennen den unbekannten Mittelwert 
. Da die Preise aus einer Normalverteilung stammen, folgt auch der Stichprobenmittelwert einer Stichprobenverteilung mit dem Mittelwert und der Varianz 
.
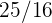b Um das Konfidenzintervall bestimmen zu können, ermitteln wir zunächst den Mittelwert der Stichprobe:
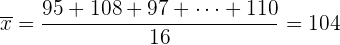
Die Formel lautet also
,
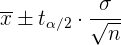wobei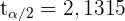 
aus einer studentschen t-Verteilung mit 
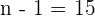Freiheitsgraden stammt. Somit ist das Konfidenzintervall
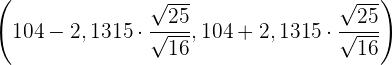
Das heißt
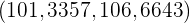
Der Mittelwert der Körpergröße einer Zufallsstichprobe von 400 Personen beträgt 1, 75 m. Die Körpergröße der Personen dieser Stadt ist eine Zufallsvariable, die einer Normalverteilung mit Varianz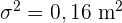 
folgt.
a Erstelle ein 95-%-Intervall für den Mittelwert der Körpergrößen der Personen.
b Wie groß müsste die Stichprobe mindestens sein, damit der wahre Mittelwert der Körpergrößen mit einem Konfidenzniveau von 90 % innerhalb von 2 cm vom Stichprobenmittelwert liegt?
a Da die Stichprobe aus 400 Personen besteht, wird zur Berechnung des Konfidenzintervalls die folgende Formel verwendet:
,
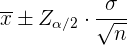wobei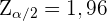 
der kritische Wert einer Standardnormalverteilung ist.
Außderdem: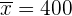 
, 
und 
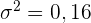. Daraus folgt, dass F
.
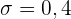Somit ist das Konfidenzintervall
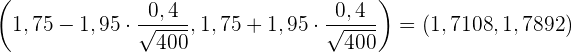
b Um den Stichprobenumfang zu ermitteln, nutzen wir 
, wobei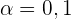 
, sodass 
.
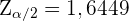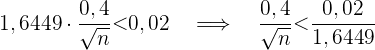
Und wenn wir 
bestimmen, erhalten wir
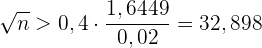
Somit ist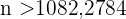 
. Das heißt, der Stichprobenumfang muss mindestens 
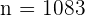umfassen.
Der monatliche Umsatz eines Haushaltswarengeschäfts folgt einer Normalverteilung mit einer Standardabweichung von 900 €. In einer statistischen Untersuchung der Verkäufe der letzten neun Monate wurde ein Konfidenzintervall für den monatlichen Durchschnittsumsatz ermittelt, dessen Extremwerte bei 4663 € und 5839 € liegen.
a Wie hoch war der durchschnittliche Umsatz in den letzten neun Monaten?
b Wie hoch ist das Konfidenzniveau für dieses Intervall?
a Bei der Berechnung des Konfidenzintervalls für den Mittelwert einer Normalverteilung liegt der Mittelwert immer in der Mitte des Intervalls. Der Mittelwert ist also
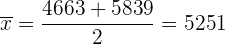
Der Mittelwert lag bei 5251 €.
b Wir haben 
, 
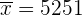und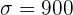 
. Daraus folgt, dass der untere Grenzwert wie folgt berechnet wird
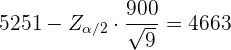
Das heißt
Und somit
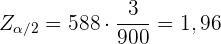
Daraus folgt, dass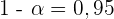 
, weshalb das Konfidenzniveau 95 % beträgt.
Wir möchten den Anteil 
der farbenblinden Personen in einer Bevölkerung anhand des Prozentsatzes schätzen, der in einer Zufallsstichprobe von Personen des Umfangs 
beobachtet wurde.
a Wenn der Prozentsatz der farbenblinden Personen in der Stichprobe 30 % beträgt, berechne den Wert von so, dass bei einem Konfidenzniveau von 0,95 der Stichprobenfehler weniger als 3,1 % beträgt.
b Wenn der Stichprobenumfang 64 Personen beträgt und der Prozentsatz der farbenblinden Personen in der Stichprobe 35 % beträgt, bestimme mit einem Signifikanzniveau von 1 % das entsprechende Konfidenzintervall für den Anteil der farbenblinden Personen.
a Das Konfidenzintervall für einen Anteil wird mit der folgenden Formel berechnet
Da das Konfidenzniveau bei 95 % liegen soll, ist 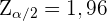. Wir erhalten
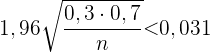
Wir berechnen und erhalten
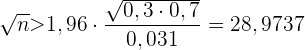
Somit ist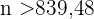 
. Das heißt, dass der Stichprobenumfang aus 840 Personen bestehen muss.
b Um das Konfidenzintervall zu ermitteln, setzen wir in
einfach die Werte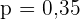 
, 
ein. Wir stellen fest, dass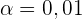 
und somit 
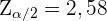. Das Konfidenzintervall ist also
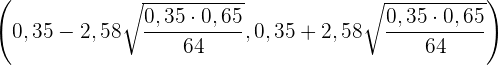
Das heißt
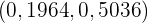
In einer Grundgesamtheit folgt eine Zufallsvariable einer Normalverteilung mit unbekanntem Mittelwert und einer Standardabweichung von 2.
a Bei einer Stichprobe von 400 Personen, die nach dem Zufallsprinzip ausgewählt wurden, wurde ein Stichprobenmittelwert von 50 ermittelt. Berechne ein Intervall mit 97%-iger Sicherheit für den Mittelwert der Grundgesamtheit.
b Welcher Mindeststichprobenumfang ist bei gleichem Konfidenzniveau erforderlich, um eine Intervallbreite von höchstens 1 zu erhalten?
Es gilt: , 
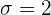, und ist unbekannt.
a Da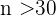 
ist, kann die Verteilung des Mittelwerts gut durch eine Normalverteilung angenähert werden. Wir wenden deshalb folgende Formel an
,
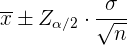wobei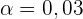 
ist. Somit ist 
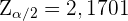. Das Konfidenzintervall ist also
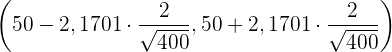
das heißt
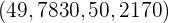
b Da wir das gleiche Konfidenzniveau haben, ist 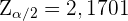. Damit die Breite des Intervalls 1 ist, müssen wir also Folgendes annehmen
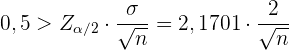
Hier bestimmen wir
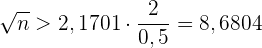
Das heißt,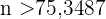 
. Daher muss der Stichprobenumfang mindestens 76 Personen betragen.
Die Zeit, die Mitarbeiter*innen an der Kasse eines Supermarktes für die Abwicklung der Kund*innen benötigen, folgt einer Normalverteilung mit unbekanntem Mittelwert und einer Standardabweichung von 0,5 Minuten. Für eine Zufallsstichprobe von 25 Kunden wurde eine durchschnittliche Zeit von 5,2 Minuten ermittelt.
a Berechne das Konfidenzintervall auf einem Niveau von 95 % für die durchschnittliche Zeit, die benötigt wird, um den Kassiervorgang von Kunden durchzuführen.
b Gib den Stichprobenumfang an, der erforderlich ist, um diese durchschnittliche Zeit mit einem Fehler von 
Minuten und einem Konfidenzniveau von 95 % zu schätzen.
a Da die Stichprobe aus 25 Kunden besteht, wird zur Berechnung des Konfidenzintervalls die folgende Formel verwendet:
,
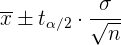wobei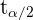 
der kritische Wert ist, sodass 
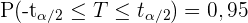ist. 
ist hierbei eine Zufallsvariable, die einer studentschen t-Verteilung mit einem Freiheitsgrad von 24 folgt.
Den Wert für 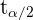können wir mit einer Tabelle der t-Verteilung oder einer Software ermitteln. Das Ergebnis ist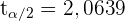 
Somit ist das Konfidenzintervall
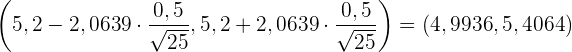
b Um den Stichprobenumfang zu ermitteln, ersetzen wir 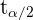durch , das aus einer Standardnormalverteilung stammt. Da der Fehler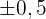 
betragen muss, gehen wir wie folgt vor
,
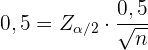wobei 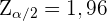ist. Wenn wir also bestimmen, erhalten wir
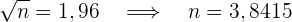
Das heißt, dass der Stichprobenumfang mindestens 
sein muss.
Die Hämoglobinmenge im menschlichen Blut folgt einer Normalverteilung mit einer Standardabweichung von 2 g/dl.
Es wurden 12 Blutabnahmen genommen und das Konfidenzintervall für den Mittelwert der Grundgesamtheit des Hämoglobins im Blut berechnet. Wenn das ermittelte Intervall zwischen 13 und 15 g/dl liegt, wie hoch ist das Konfidenzniveau dieses Intervalls?
In dieser Aufgabe ist uns das Konfidenzintervall bereits bekannt und wir sollen das Konfidenzniveau berechnen, d. h. 
.
Wir haben ,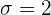 
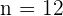und
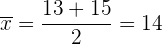
das heißt, der Mittelwert ist der Mittelpunkt des Intervalls.
Da die Stichprobe aus einer Grundgesamtheit stammt, die einer Normalverteilung folgt, wird die untere Grenze des Intervalls wie folgt berechnet
,
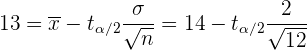da der Stichprobenumfang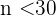 
ist. Außerdem ist 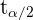der kritische Wert einer studentschen t-Verteilung mit 11 Freiheitsgraden. Wenn wir also 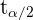bestimmen, erhalten wir
Daraus ergibt, sich dass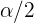 
wie folgt berechnet wird
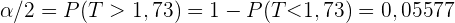
Somit sind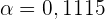 
und 
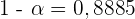. Das heißt, das Intervall hat eine Zuverlässigkeit von 88,85 %.
Hypothesentests mit Konfidenzintervallen
Eine bestimmte Nussmarke behauptet, dass höchstens 6 % der Nüsse leer sind. Es wurden 300 Nüsse nach dem Zufallsprinzip ausgewählt und 21 davon als leer befunden.
a Kann die Behauptung der Marke bei einem Signifikanzniveau von 1 % akzeptiert werden?
b Wenn der prozentuale Anteil der leeren Nüsse in der Stichprobe beibehalten wird und 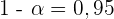ist, welcher Stichprobenumfang wäre erforderlich, um den Anteil der Nüsse mit einem Fehler von weniger als 1 % zu schätzen?
a Im ersten Unterabschnitt geht es um einen Hypothesentest, bei dem geprüft werden soll, ob ein bestimmter Anteil kleiner als ein bestimmter Wert ist. Die Nullhypothese ist also
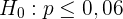
Die Alternativhypothese ist
,
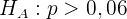wobei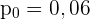 
der hypothetische Anteil ist.
Die Obergrenze des Konfidenzintervalls für den Anteil wird wie folgt berechnet:
,
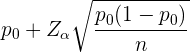da es sich um einen einseitigen Test handelt. Für diesen Fall gilt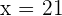 
, 
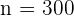und 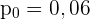. Für unsere Signifikanz von 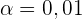ist der entsprechende kritische Wert 
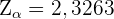. Somit ist das Konfidenzintervall
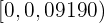
Da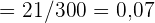 
innerhalb des Konfidenzintervalls liegt, akzeptieren wir die Nullhypothese.
Daraus schließen wir, dass höchstens 6 % der Nüsse leer sind. Das heißt, wir haben keine ausreichenden Beweise, um das Gegenteil zu behaupten.
b Der prozentuale Anteil der leeren Nüsse in der Stichprobe beträgt 7 %. Daher beträgt der Anteil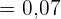 
. Der Stichprobenfehler ist
,
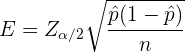der in diesem Fall kleiner als 0,01 sein soll. Außerdem ist für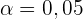 
der zugehörige kritische Wert .
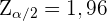Und somit
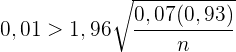
Wir bestimmen und erhalten
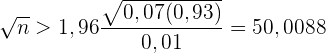
Und somit
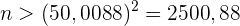
Der Umfang der Grundgesamtheit muss also größer oder gleich 2501 sein.
Die Lebensdauer der von einem Unternehmen hergestellten 100-W-Glühbirnen folgt einer Normalverteilung mit einer Standardabweichung von 120 Stunden Lebensdauer. Ihre durchschnittliche Lebensdauer beträgt garantiert mindestens 800 Stunden. Eine Stichprobe von 50 Glühbirnen wird nach dem Zufallsprinzip aus einer Charge ausgewählt, und nach der Prüfung ergibt sich eine mittlere Lebensdauer von 750 Stunden. Sollte die Charge bei einem Signifikanzniveau von 0,01 als nicht gewährleistet aussortiert werden?
Bei dieser Aufgabe geht es um einen Hypothesentest, bei dem überprüft werden soll, ob die mittlere Lebensdauer mindestens einen bestimmten Wert (800 Stunden) beträgt. Es handelt sich also um einen einseitigen Test und die Nullhypothese lautet
und die Alternativhypothese ist
,
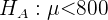wobei 
der hypothetische Mittelwert ist.
Da es sich um eine Hypothese über den Mittelwert handelt, ist das einseitige Konfidenzintervall
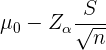
und in diesem Fall haben wir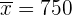 
, 
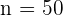, und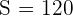 
. Außerdem entspricht die Signifikanz von 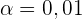einem kritischen Wert von 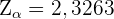. Das Konfidenzintervall ist
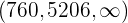
Das heißt, dass 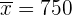nicht im Konfidenzintervall liegt und wir die Nullhypothese somit verwerfen können.
Wir kommen also zu dem Schluss, dass wir genügend Beweise haben, um die Nullhypothese zu verwerfen. Daher ist die mittlere Lebensdauer kleiner als 800 Stunden und wir können die Charge verwerfen, da die Bedingung nicht erfüllt ist.
Es ist bekannt, dass die Standardabweichung der Noten in einer bestimmten Mathematikprüfung 2,4 beträgt. Bei einer Stichprobe von 36 Studenten wurde eine Durchschnittsnote von 5,6 erzielt. Sind diese Daten geeignet, die Hypothese zu bestätigen, dass die Durchschnittsnote der Prüfung 6 war, mit einem Vertrauensniveau von 95%?
Dabei handelt es sich um einen Hypothesentest für den Mittelwert der Prüfungsnote. Das heißt, die Nullhypothese lautet
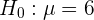
Die Alternativhypothese ist
,
wobei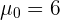 
ist. Da wir beweisen wollen, dass der Durchschnitt gleich einem bestimmten Wert ist, werden wir einen zweiseitigen Test durchführen.
Wenn wir davon ausgehen, dass die Noten annähernd normalverteilt sind, dann ist das Konfidenzintervall für
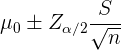
Außerdem gilt in diesem Fall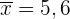 
, 
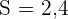und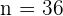 
. Da das Konfidenzintervall bei 95 % liegt und der Test zweiseitig ist, ist 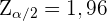. Wir haben jedoch ein Konfidenzintervall von
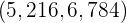
Wir akzeptieren die Nullhypothese, da 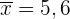innerhalb des Konfidenzintervalls liegt. Das heißt, wir akzeptieren, dass die Durchschnittsnote 6 ist.
Dies bedeutet allerdings nur, dass wir nicht genügend Beweise haben, um sagen zu können, dass die Note nicht 6 ist.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
