Name: Interaktive Aufgaben: umgekehrt proportionale Verteilungen 2
Brand: Superprof
SKU: SP-RB-00020284
Rating: 5 (1 reviews)

Löse die folgenden Probleme:

Ergebnis:

1Es soll ein Preisgeld von $\text{[math]}$ € an die drei besten Läufer eines Rennens verteilt werden, und zwar umgekehrt proportional zu den Zeiten, die sie für die Strecke benötigt haben. Der erste Läufer benötigte $\text{[math]}$ Sekunden, der zweite $\text{[math]}$ und der dritte $\text{[math]}$ .

Der erste Läufer erhält €

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 700

Der zweite Läufer erhält €

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 600

Der dritte Läufer erhält €

Dieses Feld ist erforderlich.

Lösung

1Es handelt sich um eine umgekehrt proportionale Verteilung, denn je mehr Zeit der Läufer für die Bewältigung der Strecke benötigt, desto weniger Geld erhält er. Wir gehen wie folgt vor:

$\text{[math]}$

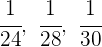
2Wir bringen auf einen gemeinsamen Nenner:

$\text{[math]}$

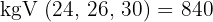
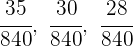
3Nun nehmen wir eine Verteilung vor, die direkt proportional zu den Zählern ist:

$\text{[math]}$

Wir erhalten die folgenden Gleichungen, aus denen wir die gewünschten Werte berechnen können

$\text{[math]}$

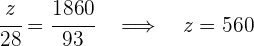
4Wir haben also:

Der erste Läufer erhält: $\text{[math]}$ €

Der zweite Läufer erhält: $\text{[math]}$ €

Der dritte Läufer erhält: $\text{[math]}$ €

2Es wird beschlossen, einen Bahnhof im Umland von Augsburg zu bauen. Die Kosten belaufen sich auf 1,7 Millionen Euro, und es wird vereinbart, dass diese von den drei Hauptorten proportional zu ihrer Entfernung vom Bahnhof getragen werden. Ort 1 befindet sich 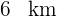$\text{[math]}$ , Ort 2 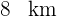$\text{[math]}$ und Ort 3 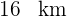$\text{[math]}$ von dem Bahnhof entfernt.

Ohne Berechnungen durchzuführen, kannst du sagen, welches Dorf das meiste Geld beisteuern muss?

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : Ort 1

b Wie hoch ist der zu zahlende Betrag für jeden Ort?

Ort 1: €

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 800000

Ort 2: €

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 600000

3Drei Freunde gewinnen einen Preis von $\text{[math]}$ €. Der Preis wird umgekehrt proportional zur Anzahl der Ruhezeiten jedes einzelnen Mitglieds verteilt. Wenn das erste Mitglied $\text{[math]}$ Stunden ruhte, das zweite $\text{[math]}$ und das dritte $\text{[math]}$ , wie viel erhält jedes Mitglied?

Ort 3: €

Dieses Feld ist erforderlich.

Lösung

1Da es sich um eine umgekehrt proportionale Verteilung handelt, muss die Ortschaft, die am nächsten an der Station liegt, also Ort 1, den größten finanziellen Beitrag leisten.

2Wir gehen wie folgt vor:

$\text{[math]}$

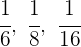
2Wir bringen auf einen gemeinsamen Nenner:

$\text{[math]}$

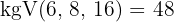
3Nun nehmen wir eine direkt proportionale Verteilung der Zähler vor:

$\text{[math]}$

Wir erhalten die folgenden Gleichungen, aus denen wir die gewünschten Werte berechnen können

$\text{[math]}$

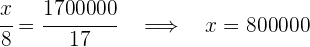
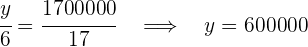
4Somit haben wir:

Ort 1: 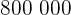$\text{[math]}$ €

Ort 2: 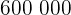$\text{[math]}$ €

Ort 3: $\text{[math]}$ €

Das erste Mitglied erhält €

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 600

Das zweite Mitglied erhält €

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 400

Das zweite Mitglied erhält €

Dieses Feld ist erforderlich.

Lösung

1Es handelt sich um eine umgekehrt proportionale Verteilung, denn je mehr Ruhezeit, desto de descanso weniger Geld wird erhalten. Wir gehen wie folgt vor:

$\text{[math]}$

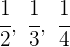
2Wir bringen auf einen gemeinsamen Nenner:

$\text{[math]}$

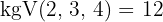
3Nun nehmen wir eine Verteilung vor, die direkt proportional zu den Zählern ist:

$\text{[math]}$

Wir erhalten die folgenden Gleichungen, aus denen wir die gewünschten Werte berechnen können

$\text{[math]}$

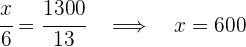
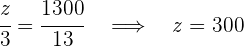
4Somit haben wir:

Preis für den 1. Läufer: $\text{[math]}$ €

Preis für den 2. Läufer: $\text{[math]}$ €

Preis für den 3. Läufer: $\text{[math]}$ €

4Es werden $\text{[math]}$ € unter drei Mitarbeitern als Gehalt ausgezahlt, und zwar umgekehrt proportional zur Anzahl der nicht gearbeiteten Tage. Der erste Mitarbeiter hat $\text{[math]}$ Tage nicht gearbeitet, der zweite $\text{[math]}$ Tage und der dritte $\text{[math]}$ Tage. Wie viel erhält jeder Mitarbeiter?

Der 1. Mitarbeiter erhält €

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 1200

Der 2. Mitarbeiter erhält €

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 2000

Der 3. Mitarbeiter erhält €

Dieses Feld ist erforderlich.

Lösung

1Es handelt sich um eine umgekehrt proportionale Verteilung, denn je mehr nicht gearbeitete Tage, desto weniger Geld erhalten die Mitarbeiter. Wir gehen wie folgt vor:

$\text{[math]}$

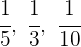
2Wir bringen auf einen gemeinsamen Nenner:

$\text{[math]}$

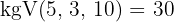
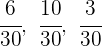
3Nun nehmen wir eine Verteilung vor, die direkt proportional zu den Zählern ist:

$\text{[math]}$

Wir erhalten die folgenden Gleichungen, aus denen wir die gewünschten Werte berechnen können

$\text{[math]}$

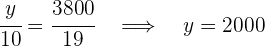
4Somit haben wir:

Mitarbeiter 1: 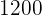$\text{[math]}$ €

Mitarbeiter 2: $\text{[math]}$ €

Mitarbeiter 3: $\text{[math]}$ €

5Eine Lehrerin verteilt $\text{[math]}$ Hausaufgaben unter drei ihrer Schüler, und zwar umgekehrt proportional zur Anzahl der erzielten Punkte. Wenn der erste Schüler eine Punktzahl von $\text{[math]}$ hat, der zweite $\text{[math]}$ und der dritte $\text{[math]}$ , wie viele müssen die Schüler dann machen?

Schüler 1 erhält Aufgaben.

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 9

Schüler 2 erhält Aufgaben.

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 6

Schüler 3 erhält Aufgaben

Dieses Feld ist erforderlich.

Lösung

1Es handelt sich um eine umgekehrt proportionale Verteilung, denn je höher die Punktzahl, desto weniger Aufgaben. Wir gehen wie folgt vor:

$\text{[math]}$

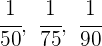
2Wir bringen auf einen gemeinsamen Nenner:

$\text{[math]}$

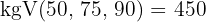
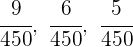
3Nun nehmen wir eine Verteilung vor, die direkt proportional zu den Zählern ist:

$\text{[math]}$

Wir erhalten die folgenden Gleichungen, aus denen wir die gewünschten Werte berechnen können

$\text{[math]}$

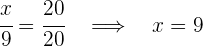
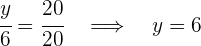
4Somit haben wir:

Schüler 1: $\text{[math]}$ Aufgaben

Schüler 2: $\text{[math]}$ Aufgaben

Schüler 3: $\text{[math]}$ Aufgaben

6 $\text{[math]}$ Bonbons werden unter drei Kindern umgekehrt proportional zu ihrem Alter verteilt. Wenn das erste Kind $\text{[math]}$ Jahre alt ist, das zweite $\text{[math]}$ und das dritte $\text{[math]}$ , wie viele Bonbons erhält jedes Kind?

Das 5-Jährige Kind bekommt Bonbons.

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 18

Das 6-Jährige Kind bekommt Bonbons.

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 15

Das 10-Jährige Kind bekommt Bonbons.

Dieses Feld ist erforderlich.

Lösung

1Es handelt sich um eine umgekehrt proportionale Verteilung, denn je älter, desto weniger Bonbons. Wir gehen wie folgt vor:

$\text{[math]}$

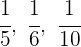
2Wir bringen auf einen gemeinsamen Nenner:

$\text{[math]}$

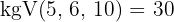
3Nun nehmen wir eine Verteilung vor, die direkt proportional zu den Zählern ist:

$\text{[math]}$

Wir erhalten die folgenden Gleichungen, aus denen wir die gewünschten Werte berechnen können

$\text{[math]}$

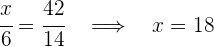
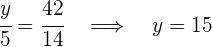
4Somit haben wir:

Das 5-jährige Kind bekommt $\text{[math]}$ Bonbons.

Das 6-jährige Kind bekommt $\text{[math]}$ Bonbons.

Das 10-jährige Kind bekommt $\text{[math]}$ Bonbons.

7In einem dreiköpfigen Team wird ein Produktivitätsbonus von $\text{[math]}$ € umgekehrt proportional zur Anzahl der im gesamten Vorjahr aufgetretenen Fehler verteilt. Wenn das erste Team-Mitglied $\text{[math]}$ Fehler verursacht, das zweite $\text{[math]}$ und das dritte $\text{[math]}$ , wie hoch ist dann die Fehlerquote jedes einzelnen Team-Mitglieds?

Das 1. Team-Mitglied erhält €.

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 3000

Das 2. Team-Mitglied erhält €.

Dieses Feld ist erforderlich.

Lösung

Die Antwort ist : 1500

Das 3. Team-Mitglied erhält €.

Dieses Feld ist erforderlich.

Lösung

1Es handelt sich um eine umgekehrt proportionale Verteilung, denn je mehr Fehler, desto weniger Bonus. Wir gehen wie folgt vor:

$\text{[math]}$

2Wir bringen auf einen gemeinsamen Nenner:

$\text{[math]}$

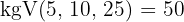
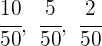
3Nun nehmen wir eine Verteilung vor, die direkt proportional zu den Zählern ist:

$\text{[math]}$

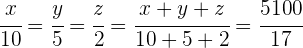
Wir erhalten die folgenden Gleichungen, aus denen wir die gewünschten Werte berechnen können

$\text{[math]}$

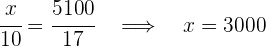
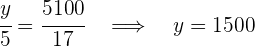
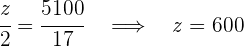
4Somit haben wir:

Das 1. Team-Mitglied erhält 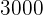$\text{[math]}$ €

Das 2. Team-Mitglied erhält $\text{[math]}$ €

Das 3. Team-Mitglied erhält $\text{[math]}$ €

Du findest diesen Artikel toll? Vergib eine Note!

5,00 (1 Note(n))

Katrin S.

Ich bin staatlich geprüfte Übersetzerin & Dolmetscherin mit den Arbeitssprachen Englisch, Spanisch, Deutsch. Meine Ausbildung habe ich am SDI München mit dem Fachgebiet Technik abvsolviert und übersetze hauptsächlich im technischen sowie mathematisch-naturwissenschaftlichen Bereich. Bei Superprof darf ich die Mathe-Expert*innen unterstützen, indem ich ihre Artikel ins Deutsche übersetze.

Interaktive Aufgaben: umgekehrt proportionale Verteilungen 2

Zinseszins – Aufgaben und Problemstellungen mit Lösungen

Umgekehrt proportionale Verteilungen

Der Dreisatz – interaktive Übungen

Interaktive Aufgaben zum Dreisatz

Ejercicios interactivos: repartos directamente proporcionales