Wähle die korrekte Option:
kgV (32, 24) = 96 und 288 sind ein Vielfaches von 32 und 24. Somit können wir bestätigen...
Bitte wähle eine Antwort aus.
kgV (20, 15) = 60 und 160 sind ein Vielfaches von 20. Somit...
Bitte wähle eine Antwort aus.
kgV (15, 28) = 1. Entonces,...
Bitte wähle eine Antwort aus.
Ohne Berechnung können wir sagen, dass das kgV (24, 48) =...
Bitte wähle eine Antwort aus.
kgV (a, a · 8) = ...
Bitte wähle eine Antwort aus.
kgV (27, 18) = 54 und 27 · 18 = 486. Somit,...
Bitte wähle eine Antwort aus.
Wenn kgV (a, b) = 8, kgV (a, b) = 2 und a = 2,...
Bitte wähle eine Antwort aus.
kgV (a, b) = 16. Somit,...
Bitte wähle eine Antwort aus.
Löse die folgenden Problemstellungen:
Jonas und Angela sind Ärzte in einem Krankenhaus mit einem großen Personalbestand. Seine Nachtschichten sind alle 8 Tage und ihre alle 6 Tage. Wenn sie heute dieselbe Schicht haben, in wie vielen Tagen werden die beiden Ärzte dann wieder gemeinsam Nachtschicht haben?
Innerhalb von Tagen.
Dieses Feld ist erforderlich.
Die Anzahl der zu vergehenden Tage muss ein Vielfaches von 8 und 6 sein.
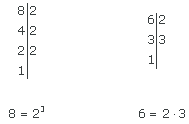
Beide gemeinsam: kgV (8,6). kgV (8, 6) = 2³ · 3 = 24
Sie haben wieder in 24 Tagen gemeinsam Nachtschicht.
Auf einer ziemlich langen geraden Strecke gibt es drei Ampeln. Die erste Ampel schaltet alle 3 Minuten auf Rot, die zweite alle 6 Minuten und die letzte alle 12 Minuten. Wenn die drei Ampeln um 13:15 Uhr gleichzeitig auf Rot schalten, kannst du die genaue Zeit angeben, zu der dies wieder der Fall ist?
Alle drei Ampeln schalten um h min auf Rot.
Dieses Feld ist erforderlich.
Die Minuten, in denen die drei Ampeln auf Rot schalten, müssen ein Vielfaches von 3, 6 und 12 sein
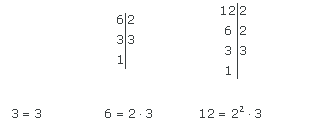
gemeinsame Vielfache der drei Ampeln: kgV (3,6,12). kgV (3, 6, 12) = 2² · 3 = 12 13 h 15' + 12' = 13 h 27'
Die drei Ampeln schalten um 13 h 27 min auf Rot.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
