Willkommen in unserem Bereich, der Aufgaben zu Korrelation und Regression gewidmet ist! Korrelation und Regression sind grundlegende Instrumente der Datenanalyse, die in einer Vielzahl von Bereichen eingesetzt werden – von der wissenschaftlichen Forschung bis zur Entscheidungsfindung in Unternehmen.
In diesem Abschnitt beschäftigen wir uns mit einer Reihe von praktischen Übungen, die dir dabei helfen sollen, die wichtigsten Konzepte im Zusammenhang mit Regression und Korrelation zu verstehen und anzuwenden. Hier erwarten dich spannende und herausfordernde Beispiele, in denen du deine Fähigkeit testen kannst, die Gleichung der Regressionsgeraden zu bestimmen, den linearen Korrelationskoeffizienten zu berechnen, Varianzen und Kovarianzen zu bestimmen und vieles mehr.
Beginnen wir damit, uns in der faszinierenden Welt der statistischen Beziehungen zurechtzufinden und Profi auf diesem Gebiet zu werden!
Ein Unternehmen möchte den jährlichen Wert seines Gesamtumsatzes in einem bestimmten Land auf der Grundlage des Verhältnisses zwischen Umsatz und Nationaleinkommen vorhersagen. Zur Untersuchung des Verhältnisses verfügt es über die folgenden Daten:
X steht für das Nationaleinkommen in Millionen Euro und Y für den Umsatz des Unternehmens in Tausend Euro im Zeitraum von 
bis 
(jeweils einschließlich). Berechne:
1 Die Regressionsgerade von Y auf X.
2 Den linearen Korrelationskoeffizienten und seine Interpretation.
3 Wenn das Nationaleinkommen des Landes im Jahr 2001 325 Millionen Euro betrug, wie hoch ist dann der voraussichtliche Umsatz des Unternehmens in diesem Jahr?
Ein Unternehmen möchte den jährlichen Wert seines Gesamtumsatzes in einem bestimmten Land auf der Grundlage des Verhältnisses zwischen Umsatz und Nationaleinkommen vorhersagen. Zur Untersuchung des Verhältnisses verfügt es über die folgenden Daten:
X steht für das Nationaleinkommen in Millionen Euro und Y für den Umsatz des Unternehmens in Tausend Euro im Zeitraum von bis (jeweils einschließlich). Berechne:
1 Die Regressionsgerade von Y auf X.
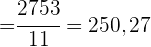
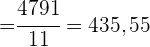
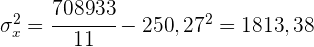
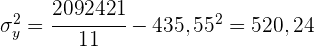
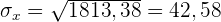
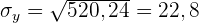
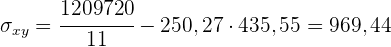
2 Den linearen Korrelationskoeffizienten und seine Interpretation.
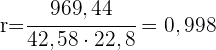
Der Korrelationskoeffizient ist positiv und liegt nahe bei 1, d. h. es besteht eine direkte und starke Korrelation.
3 Wenn das Nationaleinkommen des Landes im Jahr 2001 325 Millionen Euro betrug, wie hoch ist dann der voraussichtliche Umsatz des Unternehmens in diesem Jahr?
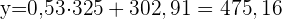
Die folgende Tabelle enthält statistische Informationen, die auf der Grundlage einer Stichprobe von 12 Betrieben über das Verhältnis zwischen der getätigten Investition und dem erzielten Ertrag in Hunderttausenden von Euro für landwirtschaftliche Betriebe gewonnen wurden: Investition (X), Ertrag (Y)
Berechne:
1 Die Regressionsgerade in Bezug auf die Rentabilität der Investition.
2 Die Investitionsprognose bei einem Kapitalertrag von 1.250.000 €.
Die nachstehende Tabelle enthält statistische Informationen, die auf der Grundlage einer Stichprobe von 12 Betrieben über das Verhältnis zwischen den getätigten Investitionen und den erzielten Erträgen in Hunderttausenden von Euro für landwirtschaftliche Betriebe gewonnen wurden:
Berechne:
1 Die Regressionsgerade in Bezug auf die Rentabilität der Investition.
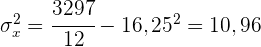
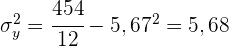
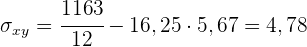
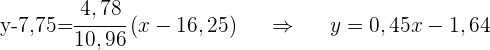
2 Die Investitionsprognose bei einem Kapitalertrag von 1.250.000 €.
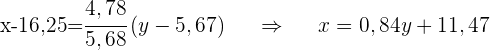
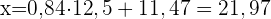
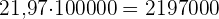
Die Anzahl der Stunden, die für das Studium eines Fachs aufgewendet wurden, und die in der entsprechenden Prüfung erzielte Note für 8 Personen lautet: Stunden (X) Note (Y)
Berechne:
1 Die Regressionsgerade von Y auf X.
2 Geschätzte Abschlussnote für eine Person, die 
Stunden gelernt hat.
Die Anzahl der Stunden, die für das Studium eines Fachs aufgewendet wurden, und die in der entsprechenden Prüfung erzielte Note für 8 Personen lautet:
Berechne:
1 Die Regressionsgerade von Y auf X.
]
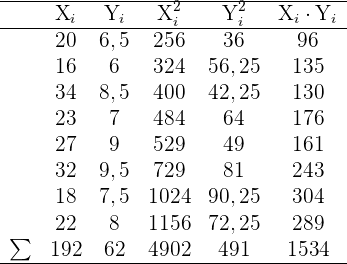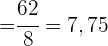
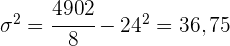
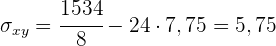
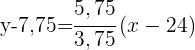
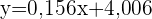
2 Geschätzte Abschlussnote für eine Person, die Stunden gelernt hat.
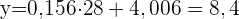
Die folgende Tabelle zeigt das Alter (in Jahren) und das aggressive Verhalten (gemessen auf einer Skala von null bis 10) von 10 Kindern. Alter Aggressives Verhalten
1 Berechne die Regressionsgerade für aggressives Verhalten in Abhängigkeit vom Alter.
2 Berechne anhand dieser Geraden den Wert für aggressives Verhalten, der einem Kind im Alter von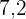 
Jahren entsprechen würde.
Die folgende Tabelle zeigt das Alter (in Jahren) und das aggressive Verhalten (gemessen auf einer Skala von null bis 10) von 10 Kindern.
1 Berechne die Regressionsgerade für aggressives Verhalten in Abhängigkeit vom Alter.
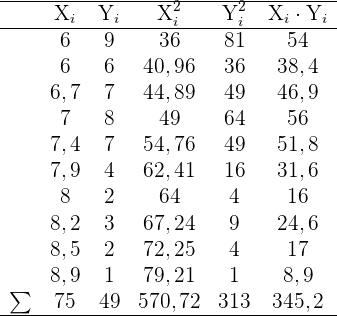
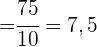
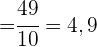
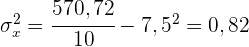
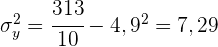
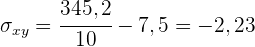
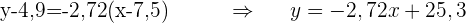
2 Berechne anhand dieser Geraden den Wert für aggressives Verhalten, der einem Kind im Alter von 7,2 Jahren entsprechen würde.
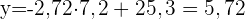
Die Werte der beiden Variablen X und Y sind gemäß der folgenden Tabelle verteilt:
Berechne:
1 Die Kovarianz.
2 Berechne und interpretiere den linearen Korrelationskoeffizienten.
3 Die Gleichung der Regressionsgeraden von Y auf X.
Die Werte der beiden Variablen X und Y sind gemäß der folgenden Tabelle verteilt:
Folgendes wird verlangt:
1 Berechne die Kovarianz.
Wir wandeln die Tabelle in eine einfache Tabelle um.
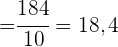
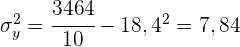
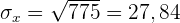
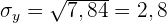
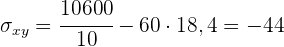
2 Berechne und interpretiere den linearen Korrelationskoeffizienten.
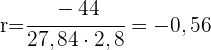
Es handelt sich um eine schwache negative Korrelation.
3 Die Gleichung der Regressionsgeraden von Y auf X.
Eine Gruppe von Studierenden hat in einer Testreihe zur Messung der sprachlichen Fähigkeiten (X) und des abstrakten Denkens (Y) folgende Ergebnisse erzielt:
Folgendes wird verlangt:
1 Gibt es eine Korrelation zwischen den beiden Variablen?
2 Wenn eine*r dieser Studierenden 
Punkte im abstrakten Denken erreicht, wie hoch wird dann seine/ihre sprachliche Ausdrucksfähigkeit eingeschätzt?
Eine Gruppe von Studierenden hat in einer Testreihe zur Messung der sprachlichen Fähigkeiten (X) und des abstrakten Denkens (Y) folgende Ergebnisse erzielt:
Folgendes wird verlangt:
1 Gibt es eine Korrelation zwischen den beiden Variablen?
Wir wandeln die Tabelle in eine einfache Tabelle um.
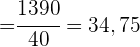
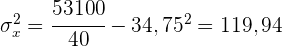
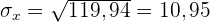
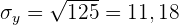
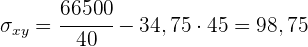
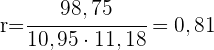
Es besteht eine starke positive Korrelation.
2 Wenn eine*r dieser Studierenden Punkte im abstrakten Denken erreicht, wie hoch wird dann seine/ihre sprachliche Ausdrucksfähigkeit eingeschätzt?
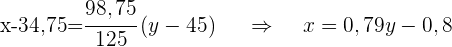
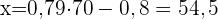
Es ist bekannt, dass es keinen Zusammenhang zwischen dem Papierverbrauch und der Anzahl der in einer Stadt gesammelten Liter Wasser pro Quadratmeter gibt.
1 Wie hoch ist der Wert der Kovarianz dieser Variablen?
2 Was ist der Wert des linearen Korrelationskoeffizienten?
3 Wie lauten die Gleichungen der beiden Regressionsgeraden und wie ist ihre Lage in der Ebene?
Es ist bekannt, dass es keinen Zusammenhang zwischen dem Papierverbrauch und der Anzahl der in einer Stadt gesammelten Liter Wasser pro Quadratmeter gibt.
1 Wie hoch ist der Wert der Kovarianz dieser Variablen?
2 Was ist der Wert des linearen Korrelationskoeffizienten?
3 Wie lauten die Gleichungen der beiden Regressionsgeraden und wie ist ihre Lage in der Ebene?
Die Geraden sind parallel zu den Achsen und stehen senkrecht zueinander.
Vier Fahrer arbeiten in einem Transportunternehmen. Die Jahre des Führerscheinalters und die Anzahl der im letzten Jahr von jedem von ihnen begangenen Verstöße sind wie folgt:
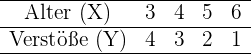
Berechne den linearen Korrelationskoeffizienten und interpretiere ihn.
Vier Fahrer arbeiten in einem Transportunternehmen. Die Jahre des Führerscheinalters und die Anzahl der im letzten Jahr von jedem von ihnen begangenen Verstöße sind wie folgt:
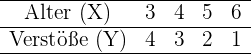
Berechne den linearen Korrelationskoeffizienten und interpretiere ihn.
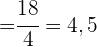
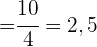
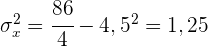
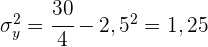
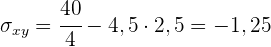
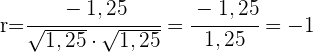
Es besteht eine perfekte inverse Korrelation.
Eine Person füllt ein wöchentliches Tippspiel und einen einfachen Lottoschein aus und notiert die Anzahl der richtigen Tipps. Während der vier Wochen im Februar waren die Treffer:
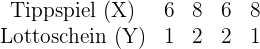
Bestimme den linearen Korrelationskoeffizienten und interpretiere ihn. Sind die mit den Regressionsgeraden erstellten Prognosen zuverlässig?
Eine Person füllt ein wöchentliches Tippspiel und einen einfachen Lottoschein aus und notiert die Anzahl der richtigen Tipps. Während der vier Wochen im Februar waren die Treffer:
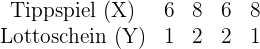
Berechne den linearen Korrelationskoeffizienten und interpretiere ihn. Sind die mit den Regressionsgeraden erstellten Prognosen zuverlässig?
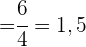
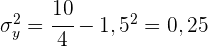
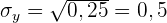
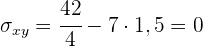
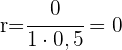
Es besteht keine Korrelation zwischen den beiden Variablen, sodass die mit den Regressionsgeraden vorgenommenen Schätzungen nicht aussagekräftig sind.
Wir haben eine Tabelle, die zwei Variablen wie folgt in Beziehung setzt:
Folgendes wird verlangt:
1 Ermittle die Kovarianz und die Standardabweichung.
2 Berechne den linearen Korrelationskoeffizienten.
Wir haben eine Tabelle, die zwei Variablen wie folgt in Beziehung setzt:
Folgendes wird verlangt:
1 Ermittle die Kovarianz und die Standardabweichung.
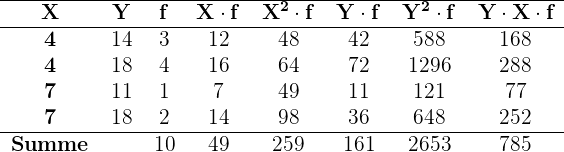
Die Standardabweichung der einzelnen Variablen ist somit
und die Kovarianz ist
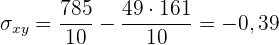
2 Berechne den linearen Korrelationskoeffizienten.
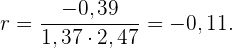
Das heißt, es besteht eine schwache inverse Korrelation.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
