Linearer Korrelationskoeffizient
Der lineare Korrelationskoeffizient ist der Quotient aus der Kovarianz und dem Produkt der Standardabweichungen beider Variablen.
Der lineare Korrelationskoeffizient wird mit dem Buchstaben 
angegeben.
Eigenschaften
1 Der Korrelationskoeffizient ändert sich nicht, wenn die Messgröße variiert.
Das heißt, wenn wir die Höhe in Metern oder Zentimetern ausdrücken, ändert sich der Korrelationskoeffizient nicht.
2 Das Vorzeichen des Korrelationskoeffizienten ist das gleiche wie das der Kovarianz.
Wenn die Kovarianz positiv ist, ist die Korrelation direkt.
Ist die Kovarianz negativ, ist die Korrelation invers.
Wenn die Kovarianz null ist, besteht keine Korrelation.
3 Der lineare Korrelationskoeffizient ist eine reelle Zahl zwischen 
und 
.
4 Wenn der lineare Korrelationskoeffizient Werte nahe annimmt, ist die Korrelation stark und invers, und ist umso stärker, je näher sich der Wert bei befindet.
5 Wenn der lineare Korrelationskoeffizient Werte nahe annimmt, ist die Korrelation la correlación es stark und direkt, und ist umso stärker, je näher sich der Wert bei befindet.
6 Wenn der lineare Korrelationskoeffizient Werte nahe 
annimmt, ist die Korrelation schwach.
7 Wenn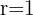 
oder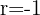 
, liegen die Punkte des Streudiagramms oberhalb der fallenden oder steigenden Geraden. Zwischen beiden Variablen besteht eine funktionale Abhängigkeit.
Beispiele
Beispiel 1
Die Punktzahlen von 
Schüler*innen einer Klasse in den Fächern Mathe und Physik sind wie folgt:
Den Korrelationskoeffizienten der Verteilung ermitteln und interpretieren.
1 Wir fügen der Tabelle 
Spalten mit 
, 
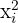und 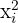hinzu. Die letzte Zeile der Tabelle ergibt sich aus der Summe der Werte jeder Spalte:
2 Wir berechnen die arithmetischen Mittel.
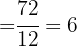
3 Wir berechnen die Kovarianz.
4 Wir berechnen die Standardabweichungen
5 Wir wenden die Formel des linearen Korrelationskoeffizienten an.
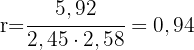
Da der Korrelationskoeffizient positiv ist, ist die Korrelation direkt.
Und da der Korrelationskoeffizient sehr nahe bei 1 liegt, ist die Korrelation sehr stark.
Beispiel 2
Die Werte zweier Variablen 
und 
verteilen sich laut der folgenden Tabelle:
Bestimme den Korrelationskoeffizienten.
1 Wir wandeln die Tabelle mit doppeltem Eintrag in eine einfache Tabelle um.
latex]\sigma _{x}=\sqrt{2}=1,41[/latex] 
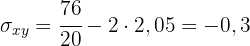
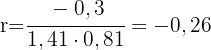
Da der Korrelationskoeffizient negativ ist, ist die Korrelation invers.
Da der Korrelationskoeffizient sehr nahe bei 0 liegt, ist die Korrelation sehr schwach.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
