Kapitel
Monotonie, Konvergenz, Divergenz und Schranken von Folgen
Untersuche Monotonie, Konvergenz, Divergenz und die Schranken der Folgen
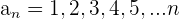
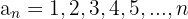
Steigend
Nach unten beschränkt
Untere Schranken: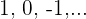 
Das Minimum ist 
Nicht nach oben beschränkt
Divergent
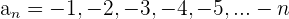
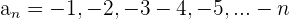
Fallend
Nach oben beschränkt
Obere Schranken: 
Das Maximum ist 
Nicht nach unten beschränkt
Divergent
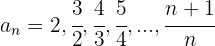
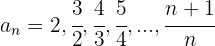
Fallend
Nach oben beschränkt
Obere Schranken: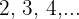 
Das Maximum ist 
Nach unten beschränkt
Untere Schranken: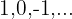 
Das Infimum ist
Konvergent: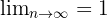 
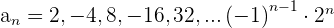
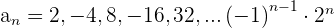
Nicht monoton
Nicht beschränkt
Nicht konvergent, nicht divergent
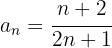
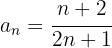
Die ersten Terme dieser Folge sind:
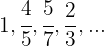
Streng monoton fallend
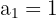
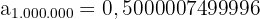
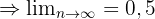
Konvergente Folge
Da fallend, ist eine obere Schranke und somit das Maximum.
ist eine untere Schranke und somit das Infimum.
Die Folge ist somit beschränkt
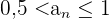
Die ersten Terme der Folge sind:
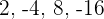
Nicht monoton
Nicht konvergent, nicht divergent
Nicht beschränkt
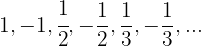
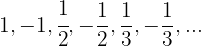
Nicht monoton
Sie ist konvergent, da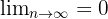 
Nach oben beschränkt, ist das Maximum
Nach unten beschränkt, ist das Minimum
Beschränkt
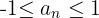
Die ersten Terme der Folge sind:
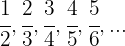
Sie ist streng monoton fallend
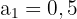
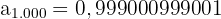
Konvergente Folge
Nach unten beschränkt, 
ist das Minimum
Nach oben bechränkt, ist das Supremum
Die Folge ist also beschränkt
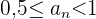
Bestimme das allgemeine Glied der folgenden Folgen
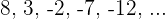
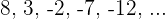
Wir können die Differenz zwischen aufeinanderfolgenden Gliedern ermitteln:
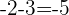
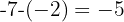
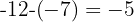
Da die Differenz konstant ist, gilt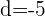 
Es handelt sich um eine arithmetische Folge
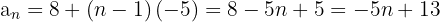
Wir können jedes Glied durch das vorherige Glied dividieren:
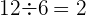
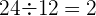
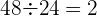
Da der Quotient konstant ist, gilt 
Es handelt sich um eine geometrische Folge
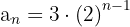
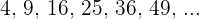
Die Folge kann auch wie folgt geschrieben werden:
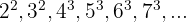
Wir stellen fest, dass die Basen eine arithmetische Folge sind, wobei 
und der Exponent konstant ist. Wir können also folgende Folge für die Basis schreiben:
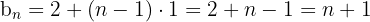
Das allgemeine Glied ist also:
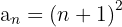
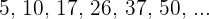
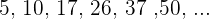
Jedes Glied dieser Folge ist das darauffolgende Glied der Glieder der vorhergehenden Folge, so dass wir sie umschreiben können als:
Wir bestimmen das allgemeine Glied, wie wir es im vorherigen Fall gesehen haben, und addieren 1.
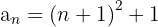
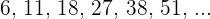
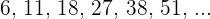
Die Folge kann auch wie folgt geschrieben werden:
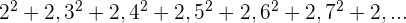
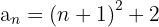
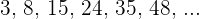
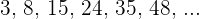
Die Folge kann auch wie folgt geschrieben werden:
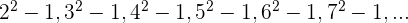
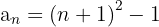
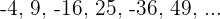
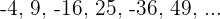
Jedes Glied dieser Folge ist die Umkehrung eines jeden Gliedes der Folge 
, wesbhalb:
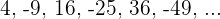
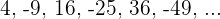
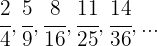
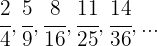
Wir haben zwei Folgen. Eine für den Zähler und eine für den Nenner:
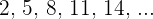
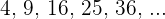
Die erste Folge ist eine arithmetische Folge mit 
, bei der zweiten Folge handelt es sich um Quadratzahlen.
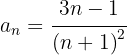
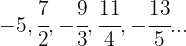
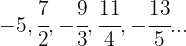
Wenn wir das Vorzeichen außer Acht lassen, ist der Zähler eine arithmetische Folge mit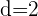 
.
Der Nenner ist eine arithmetische Folge von .
Da die ungeraden Glieder negativ sind, multiplizieren wir mit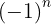 
.
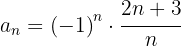
Berechne das allgemeine Glied der folgenden Folgen
Der Zähler ist konstant.
Der Nenner ist eine arithmetische Folge von .
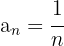
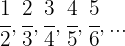
Der Zähler ist eine arithmetische Folge mit
Der Nenner ist eine arithmetische Folge mit
Wenn wir jedes Glied der Folge in rationaler Form schreiben, erhalten wir:
Der Zähler ist eine arithmetische Folge mit
Der Nenner ist eine arithmetische Folge von
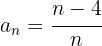
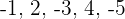
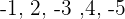
Wenn wir das Vorzeichen außer Acht lassen, handelt es sich um eine arithmetische Folge mit
Da die ungeraden Glieder negativ sind, multiplizieren wir mit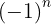
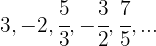
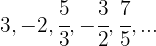
Die Folge kann auch wie folgt geschrieben werden:
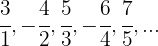
Wenn wir das Vorzeichen außer Acht lassen, ist der Zähler eine arithmetische Folge mit
Der Nenner ist eine arithmetische Folge von
Da die geraden Glieder negativ sind, multiplizieren wir mit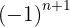 
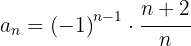
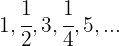
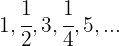
Die Folge ist oszillierend
Die ungeraden Glieder bilden eine arithmetische Folge mit , wenn wir die geraden Terme außer Acht lassen
Der Nenner der geraden Glieder bilden eine arithmetische Folge mit
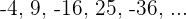
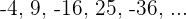
Die Folge kann auch wie folgt geschrieben werden:
Wenn wir das Vorzeichen und den Exponenten außer Acht lassen, haben wir eine arithmetische Folge mit
Da die Glieder zum Quadrat stehen, müssen wir das allgemeine Glied quadrieren
Da die ungeraden Glieder negativ sind, multiplizieren wir mit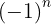
Die Folge kann auch wie folgt geschrieben werden:
Die Folge ist oszillierend
Die Zähler der ungeraden Glieder bilden eine arithmetische Folge mit , wenn wir die geraden Glieder außer Acht lassen.
Da die Glieder zum Quadrat stehen, müssen wir das allgemeine Glied quadrieren
Der erste Summand des Nenners (wir lassen das Quadrat außer Acht) ist eine arithmetische Folge von (ohne die geraden Glieder zu zählen)
Wir müssen das allgemeine Glied quadrieren und addieren
Die geraden Glieder bilden eine konstante Folge.
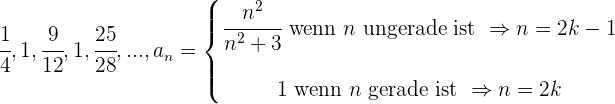
Wir trennen die Folgen des Zählers und des Nenners und erhalten:
Zähler: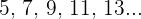 
Nenner: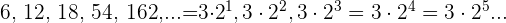 
Der Zähler ist eine arithmetische Folge mit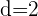
Der Nenner ist eine geometrische Folge mit
Wenn wir das Vorzeichen außer Acht lassen, ist der Zähler eine arithmetische Folge mit
Der Nenner ist eine geometrische Folge mit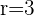 
Da die geraden Glieder negativ sind, multiplizieren wir mit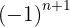
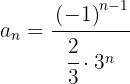
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
