Kapitel
Was ist die Punktschätzung?
Eine Punktschätzung ist eine Zahl, die wir anhand einer Stichprobe berechnen. Diese Zahl wird auch Punktschätzer genannt. Daher verwenden wir diesen Punktschätzer, um den entsprechenden Parameter der Grundgesamtheit zu schätzen.
Beispiel: In der südspanischen Stadt Tarifa wird eine Umfrage unter 500 jungen Menschen im Alter von 8 bis 25 Jahren durchgeführt. Aus der Umfrage geht hervor, dass 89 % der jungen Menschen Kitesurfen betreiben. Da nicht alle jungen Menschen in der Stadt befragt wurden, kann man sagen, dass 89 % eine Punktschätzung des wahren Prozentsatzes der Grundgesamtheit ist.
Daher können wir sagen, dass etwa 89% der jungen Leute in Tarifa Kitesurfen praktizieren.
Beispiel: Gemessen wird die Lebensdauer von 40 Glühbirnen mit 60 W aus einer bestimmten Charge. Bei der Berechnung der durschnittlichen Lebensdauer erhält man 
Stunden. Da die Lebensdauer nicht für alle 1.000 Glühbirnen der Charge gemessen wurde, ist 
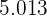eine Punktschätzung für die durchschnittliche Lebensdauer der Charge.
Was ist der Stichprobenfehler?
Die Wahrscheinlichkeit, dass es einen Stichprobenfehler gibt, existiert immer.
Der Stichprobenfehler ist die Differenz zwischen einem Schätzwert, der anhand einer Stichprobe berechnet wurde, und dem Wert des entsprechenden Parameters in der Grundgesamtheit. Da der Fehler immer positiv ist, wird der Betrag dieser Differenz genommen.
Es ist wichtig, dass dieser Stichprobenfehler im Entscheidungsprozess berücksichtigt wird. Schließlich dienen viele der erlernten statistischen Instrumente dazu, uns bei der Entscheidungsfindung zu helfen.
Ein Merkmal des Stichprobenfehlers ist, dass er mit zunehmendem Stichprobenumfang kleiner wird. Aus diesem Grund wird empfohlen, die Stichprobe so groß wie möglich zu wählen.
Die durchschnittliche Körpergröße der Frauen in Spanien beträgt beispielsweise 163,4 cm. Nehmen wir an, dass wir bei einer Stichprobe von 1.000 Frauen eine durchschnittliche Körpergröße von 164,6 cm erhalten. Somit lautet der Stichprobenfehler
Das heißt, der Stichprobenfehler liegt bei 1,2 cm.
Was ist das Konfidenzintervall?
Im Allgemeinen kann ein Stichprobenfehler nicht ausgeschlossen werden. Daher verwenden wir ein Konfidenzintervall, um mit dem Fehler umzugehen.
Definition eines Konfidenzintervalls
Wir definieren eine Wahrscheinlichkeit 
. Wir möchten ein Intervall konstruieren, in dem der reelle Parameter der Grundgesamtheit mit einer Wahrscheinlichkeit im Intervall liegt. Dieses Intervall ist durch zwei Zahlen 
und 
definiert und wird als Konfidenzintervall mit dem Konfidenzniveau bezeichnet. Das Intervall wird gewöhnlich als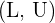 
bezeichnet
Die Wahrscheinlichkeit wird gewöhnlich als 
geschrieben, wobei 
das Signifikanzniveau ist.
Beispiel: Nehmen wir an, dass im Beispiel der 60-W-Glühbirnen das 95%-Konfidenzintervall 
beträgt. Daher wissen wir, dass die durchschnittliche Lebensdauer der gesamten Charge mit 95%iger Wahrscheinlichkeit zwischen 4.799 und 5.227 Stunden liegt.
Abweichung des Konfidenzintervalls
Die Standardabweichung 
ist ein Maß für die Abweichung der Daten in der Grundgesamtheit oder Stichprobe. Daher ist klein, wenn alle Daten einander sehr ähnlich sind; andererseits ist groß, wenn die Daten stark voneinander abweichen.
Die Standardabweichung einer endlichen Grundgesamtheit/Stichprobe wird wie folgt berechnet
,
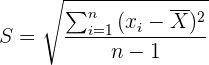wobei 
der Mittelwert der Stichprobe und 
die Anzahl der Elemente der Stichprobe ist. Die Standardabweichung der Grundgesamtheit wird mit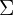 
notiert, die Abweichung der Stichprobe mit .
Wenn wir eine Stichprobe 
erhalten, wäre die Schätzung des Mittelwerts . Nimmt man jedoch eine andere Stichprobe 
, so lautet die Schätzung 
. Das heißt, auch die Punktschätzungen variieren; daher ist es sinnvoll, die Standardabweichung für die Schätzer zu definieren.
Wenn wir die Standardabweichung der ursprünglichen Grundgesamtheit kennen, dann ist die Standardabweichung des Mittelwerts
,
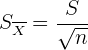wobei der Umfang der Stichprobe ist. Bei den Punktschätzern wird die Standardabweichung oft als Standardfehler bezeichnet.
Aus der obigen Gleichung geht hervor, dass die Abweichung 
der Schätzung abnimmt, wenn der Stichprobenumfang zunimmt. Mit anderen Worten: Je größer die Stichprobe ist, desto näher liegen die möglichen Schätzungen beieinander; je größer die Stichprobe ist, desto näher liegt die Schätzung am wahren Wert des Parameters der Grundgesamtheit.
Wir denken daran, dass die Standardabweichung der Grundgesamtheit/Stichprobe ist und der Standardfehler (oder Standardabweichung) der Schätzung.
Wie wird das Konfidenzintervall berechnet?
Es gibt verschiedene Möglichkeiten, Konfidenzintervalle zu berechnen; jede hängt von den uns zur Verfügung stehenden Informationen ab.
Bekannte Standardabweichung und Stichprobenumfang größer als 30
Wir nehmen an, dass wir eine Grundgesamtheit haben, deren Stichprobenumfang größer oder gleich 30 ist, d. h. 
. Außerdem nehmen wir an, dass die Standardabweichung der Grundgesamtheit ist. Somit wird das Konfidenzintervall für den Mittelwert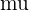 
mit einem Konfidenzniveau von wie folgt berechnet:
1 Berechne den Durchschnittswert der Stichprobe
2 Bestimme den Standardfehler der Schätzung
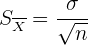
3 Ermittle den kritischen Wert 
, so dass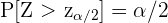 
.
Wenn wir eine Variable 
mit einer Standardverteilung haben, dann ist derjenige Wert, bei dem die Wahrscheinlichkeit, dass größer als ist,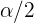 
ist. Es ist nicht einfach, diese Werte analytisch zu ermitteln, daher werden Tabellen oder Software verwendet, um sie zu bestimmen.
Die Tabelle mit den -Werten für die häufigsten findest du unten.
4 Berechne das Konfidenzintervall anhand von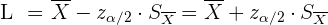 
An einigen Stellen wird das Konfidenzintervall für diesen Fall oft wie folgt zusammengefasst
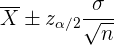
Dieser Ausdruck gibt sowohl die Untergrenze als auch die Obergrenze an.
Beispiel: Wir kehren zu dem Beispiel der 60-W-Glühlampen zurück. Es wurde eine Stichprobe von 40 Glühbirnen mit einer durchschnittlichen Lebensdauer von entnommen. Es wird angegeben, dass die Standardabweichung der Lebensdauer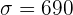 
Stunden beträgt. Um das Konfidenzintervall bei 95 % zu berechnen, müssen wir also zunächst beachten, dass 
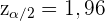. Somit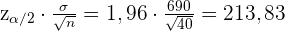 
Somit ist das Konfidenzintervall
Wir stellen fest, dass wir im obigen Beispiel zunächst die Menge berechnen
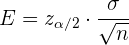
Dieser Wert wird als Fehlerspanne oder Schätzfehler bezeichnet.
Es besteht also eine Wahrscheinlichkeit von , dass unsere Schätzung höchstens einen Fehler von 
aufweist. Die Bedeutung von Konfidenzintervallen liegt darin, dass sie uns auch eine Einschätzung des Umfangs des möglichen Fehlers ermöglichen.
Unbekannte Standardabweichung
Wenn wir die Standardabweichung der ursprünglichen Grundgesamtheit nicht kennen, müssen wir eine etwas andere Strategie zur Berechnung des Konfidenzintervalls anwenden.
Das Verfahren zur Berechnung des Konfidenzintervalls lautet:
1 Berechne den Durchschnittswert der Stichprobe
2 Ermittle den Standardfehler der Stichprobe
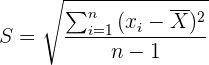
3 Berechne den kritischen Wert 
, so dass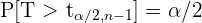 
, wobei 
einer studentschen 
-Verteilung mit 
Freiheitsgraden folgt.
In diesem Fall haben wir eine Variable mit einer studentschen -Verteilung mit Freiheitsgraden. Somit ist der Wert, bei dem die Wahrscheinlichkeit, dass größer ist als , 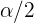beträgt. Auch hier ist es nicht einfach, diese Werte analytisch zu ermitteln, daher wird eine Software eingesetzt, um sie zu bestimmen.
4 Berechne das Konfidenzintervall anhand von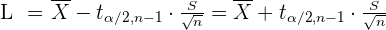 
In diesem Fall wird das Konfidenzintervall wie folgt zusammengefasst
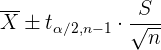
Beispiel: Nehmen wir noch einmal das Beispiel der 60-W-Glühbirnen. Wir beachten, dass eine Stichprobe von 40 Glühbirnen entnommen wurde, bei denen die durchschnittliche Lebensdauer betrug.
In diesem Fall kennen wir jedoch die Standardabweichung der Grundgesamtheit nicht. Berechnet man jedoch die Standardabweichung der 40 Glühbirnen, so erhalten wir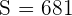 
Stunden. Um das Konfidenzintervall bei 95 % zu berechnen, müssen wir also zunächst ermitteln, das der kritische Wert einer -Verteilung mit 39 Freiheitsgraden ist. Mit Verwendung einer Software erhalten wir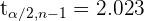 
.
Somit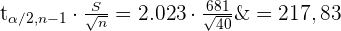 
Somit lautet das Konfidenzintervall
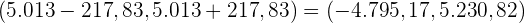
Wenn die Standardabweichung unbekannt ist, wird die Fehlerspanne wie folgt berechnet
Tabellen mit kritischen Werten und Verwendung von Statistiksoftware
Wie man sieht, müssen zur Bestimmung der Konfidenzintervalle die kritischen Werte entweder aus einer Normalverteilung oder aus einer studentschen t-Verteilung ermittelt werden.
Im Falle einer Normalverteilung sind die Werte allgemein bekannt und werden in der folgenden Tabelle für gängige -Werte zusammengefasst:
| | |
|---|---|---|
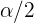| 0,90 | 0,05 | 1,645 |
| 0,95 | 0,025 | 1,96 |
| 0,99 | 0,005 | 2,575 |
Diese Werte können jedoch mithilfe von Software ermittelt werden. Bei der studentschen t-Verteilung ist es in der Tat nicht einfach, die kritischen Werte in einer Tabelle zusammenzufassen, da diese Werte je nach den Freiheitsgraden 
unterschiedlich sind.
Die folgende Liste zeigt einige Möglichkeiten zur Ermittlung der kritischen Werte:
1 Um den Wert von mit Excel zu berechnen, wird folgende Funktion genutzt:
,
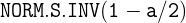wobei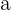 
der Wert von ist.
2 Es ist auch möglich, den -Wert mit der Statistiksoftware R zu ermitteln. In diesem Fall kommt die Funktion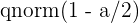 
zum Einsatz. Analog dazu sollte 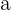den Wert annehmen, den hat.
3 Für den Fall der studentschen -Verteilung gilt: Um 
mit Excel zu erhalten, verwenden wir die Funktion
,
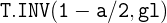wobei 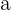der Wert von ist und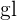 
die Freiheitsgrade .
4 Um schließlich den Wert mithilfe von R zu erhalten, wird die Funktion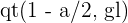 
verwendet. Wie im vorherigen Fall nimmt 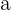den Wert von an und 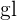sind die Freiheitsgrade .
Auswirkungen von Parameteränderungen auf das Konfidenzintervall
Zu beachten ist, dass bei der Schätzung mit Konfidenzintervallen der Stichprobenumfang und das Konfidenzniveau willkürlich festgelegt werden.
Diese Parameter werden in der Regel unter Berücksichtigung der gewünschten Genauigkeit der Schätzung zugewiesen. Wenn wir beispielsweise eine sehr genaue und zuverlässige Bestimmung wünschen, dann muss groß und klein sein; in diesem Fall muss ebenfalls groß sein. Wenn wir jedoch aufgrund von Ressourcen- oder Zeitmangel keine allzu große Stichprobe nehmen können, können wir anpassen, damit sie kleiner wird; in diesem Fall ist unsere Schätzung jedoch weniger zuverlässig.
Im Folgenden diskutieren wir die Auswirkungen dieser Parameter auf die Konfidenzintervalle.
Was passiert, wenn wir das Konfidenzniveau verändern?
Wir denken daran, dass die Fehlerspanne durch folgenden Ausdruck gegeben ist
Dabei ist zu beachten, dass und mit zunehmendem Konfidenzniveau steigen. Daher können wir das Konfidenzniveau reduzieren, um die Fehlergröße zu verringern; dies bedeutet jedoch, dass das Intervall weniger zuverlässig ist. Mit anderen Worten: Es ist wahrscheinlicher, dass unsere Schätzung außerhalb des Konfidenzintervalls liegt.
Was passiert, wenn wir den Stichprobenumfang ändern?
Andererseits können wir anhand der gleichen Fehlergleichung
feststellen, dass, wenn zunimmt, die Fehlergröße abnimmt (das Konfidenzniveau bleibt dabei gleich). Aus diesem Grund ist es ideal, wenn der Stichprobenumfang groß genug ist, um eine kleine Fehlerspanne und ein großes Konfidenzniveau zu haben.
Notwendiger Stichprobenumfang
Wenn wir von bestimmen, erhalten wir
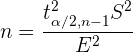
Wenn wir also einen gewünschten Fehler haben, können wir den Stichprobenumfang berechnen, der erforderlich ist, damit unsere Schätzung diesen Fehler nicht überschreitet.
Dazu ist es zunächst erforderlich, eine kleine Stichprobe zu nehmen (je nach Kontext sind sogar 15 Elemente ausreichend). Auf diese Weise schätzen wir den Stichprobenumfang , der erforderlich ist, damit unser Fehler kleiner als ist. Dann nehmen wir wieder eine Stichprobe, aber jetzt mit einem Stichprobenumfang von .
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
