Eigenschaften von Potenzen rationaler Zahlen
1Potenz einer rationalen Zahl
Bei einem Bruch, der mit einem Exponenten versehen ist, wird der Exponent als der Exponent des Zählers und des Nenners aufgeteilt.
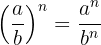
Beispiel:
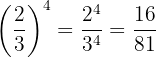
2Negativer Exponent
Bei einer rationalen Zahl mit negativem Exponenten wird der Zähler mit dem Nenner vertauscht, und der Exponent ändert sein Vorzeichen..
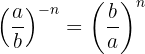
Beispiel:
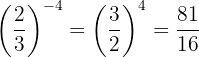
3 Exponent -1
Bei einer rationalen Zahl mit dem Exponenten -1 werden Zähler und Nenner vertauscht.
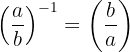
Beispiel:
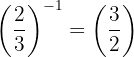
Regeln für die Exponenten bei rationalen Zahlen
Die Regeln der Exponenten gelten für alle reellen Zahlen, also auch für die rationalen Zahlen.
1Potenz 0
Eine rationale Zahl hoch 0 ist gleich der Einheit.
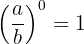
2Potenz 1
Eine rationale Zahl hoch 1 ist gleich sich selbst.
3Produkt aus Potenzen
3.1Potenzen mit gleicher Basis
Es handelt sich um eine weitere Potenz mit der gleichen Basis, deren Exponent die Summe der Exponenten ist.
Beispiel:
3.2Potenzen mit gleichem Exponenten
Bei einem Bruch, der mit einem Exponenten versehen ist, wird der Exponent als der Exponent des Zählers
Beispiel:
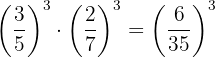
4Quotient aus Potenzen
4.1Potenzen mit gleicher Basis
Es handelt sich um eine weitere Potenz mit der gleichen Basis, deren Exponent die Differenz der Exponenten ist.
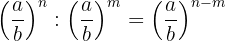
Beispiel:
4.2 Potenzen mit gleichem Exponenten
Es handelt sich um eine weitere Potenz mit dem gleichen Exponenten, deren Basis der Quotient der Basen ist.
Beispiel:
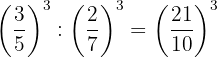
5Potenz einer Potenz
Bei einem Bruch, der mit einem Exponenten versehen ist, wird der Exponent als der Exponent des Zählers und des Nenners aufgeteilt.
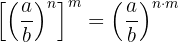
Beispiel:
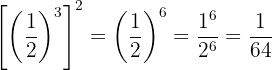
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
