Kapitel
Definition der Potenz mit positivem ganzzahligem Exponenten oder natürlicher Zahl
Die Potenz mit natürlichem Exponenten einer positiven ganzen Zahl entspricht der Multiplikation dieser Zahl mit sich selbst so oft, wie es der Exponent angibt, und ihr Vorzeichen hängt vom Vorzeichen der Basis ab.
Wenn die Basis positiv ist, ist das Ergebnis positiv.
Beispiel:
1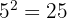 
2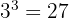 
Wenn die Basis negativ ist, lautet das Ergebnis:
Positiv 
, wenn der Exponent gerade ist.
Negativ 
, wenn der Exponent ungerade ist.
Beispiel:
1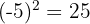 
2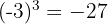 
Allgemein lässt sich sagen, dass die Potenz einer natürlichen Zahl mit einer ganzen Zahl als Exponent eine weitere ganze Zahl ist, deren Betrag dem Betrag der Potenz entspricht und deren Vorzeichen sich aus der Anwendung der folgenden Regeln ergibt:
1 Potenzen mit geraden Exponenten sind immer positiv.
gerade 
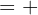
gerade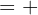
2 Potenzen mit ungeradem Exponenten haben das gleiche Vorzeichen wie die Basis.
ungerade
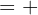
ungerade 
Eigenschaften von Potenzen ganzer Zahlen
1 Die Potenz von 
ist gleich 
.
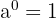
Beispiel:
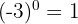
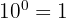
2 Die Potenz von entspricht dieser Zahl.
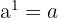
Beispiel:
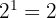
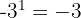
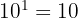
3 Produkt von Potenzen mit gleicher Basis. Es handelt sich um eine weitere Potenz mit gleicher Basis, deren Exponent die Summe der Exponenten ist.
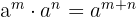
Beispiel:
4 Division von Potenzen mit gleicher Basis. Es handelt sich um eine weitere Potenz mit gleicher Basis, deren Exponent die Differenz der Exponenten ist.
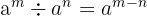
Beispiel:
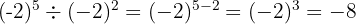
5 Potenz einer Potenz. Es handelt sich um eine weitere Potenz mit der gleichen Basis, deren Exponent das Produkt der Exponenten ist.
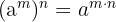
Beispiel:
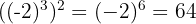
6 Produkt von Potenzen mit gleichem Exponenten. Es handelt sich um eine weitere Potenz mit gleichem Exponenten, deren Basis das Produkt der Basen ist.
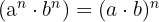
Beispiel:
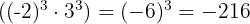
7 Quotient aus Potenzen mit gleichem Exponenten. Es handelt sich um eine weitere Potenz mit gleichem Exponenten, deren Basis der Quotient der Basen ist.
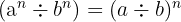
Beispiel:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
