Potenzrechnung: gemischte Aufgaben

Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Um die Potenz einer Potenz zu berechnen, multiplizieren wir die Exponenten miteinander:

Um die Potenz eines Produkts zu berechnen, verwenden wir dieselbe Hochzahl für beide Basen:

Um die Potenz einer Potenz zu berechnen, multiplizieren wir die Exponenten miteinander:

Um die Potenz einer Potenz zu berechnen, multiplizieren wir die Exponenten miteinander:

Stelle zuerst die Basis als Produkt der Primzahlen dar. Finde dann die Potenz der Potenz, indem du die Exponenten multiplizierst:

Stelle zuerst die Basis als Produkt der Primzahlen dar. Finde dann die Potenz der Potenz, indem du die Exponenten multiplizierst:

Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Um die Potenz einer Potenz zu berechnen, multiplizieren wir die Exponenten miteinander:

Um die Potenz eines Produkts zu berechnen, verwenden wir dieselbe Hochzahl für beide Basen:

Um die Potenz einer Potenz zu berechnen, multiplizieren wir die Exponenten miteinander:

Um die Potenz einer Potenz zu berechnen, multiplizieren wir zuerst die Exponenten miteinander. Bedenke dabei, dass alle Zahlen ungleich Null mit Exponent Null als Ergebnis 1 liefern:

Stelle zuerst die Basis als Produkt der Primzahlen dar. Finde dann die Potenz der Potenz, indem du die Exponenten multiplizierst:

Stelle zuerst die Basis als Produkt der Primzahlen dar. Finde dann die Potenz der Potenz, indem du die Exponenten multiplizierst:

Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

Das Ergebnis muss ein negatives Vorzeichen haben, da die Basis negativ und der Exponent eine ungerade Zahl ist.

Zerlege die Zahl 8 zuerst in Faktoren. Multipliziere dann die Potenzen mit der gleichen Basis:

Das Ergebnis muss ein positives Vorzeichen haben, da die Basis negativ und der Exponent eine gerade Zahl ist:

Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

Das Ergebnis muss ein negatives Vorzeichen haben, da die Basis negativ und der Exponent eine ungerade Zahl ist:

Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

Da der Exponent negativ ist, müssen wir den Kehrwert der Basis bilden:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Da der Exponent negativ ist, müssen wir den Kehrwert der Basis bilden:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Da der Exponent negativ ist, müssen wir den Kehrwert der Basis mit positivem Exponent bilden:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Um die Potenz einer Potenz zu berechnen, lassen wir die Basis stehen und multiplizieren die Exponenten miteinander:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Vereinfache zuerst den Ausdruck in der Klammer. Lass dafür die Basis stehen und ziehe die Exponenten voneinander ab:

Um die Potenz einer Potenz zu berechnen, lassen wir die Basis stehen und multiplizieren die Exponenten miteinander:

Das Ergebnis muss ein positives Vorzeichen haben, da die Basis negativ und der Exponent eine gerade Zahl ist:

Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

Das Ergebnis muss ein positives Vorzeichen haben, da die Basis negativ und der Exponent eine gerade Zahl ist:

Zerlege die Zahl 27 zuerst in Faktoren. Multipliziere dann die Potenzen mit der gleichen Basis:

Das Ergebnis muss ein positives Vorzeichen haben, da die Basis negativ und der Exponent eine gerade Zahl ist:

Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

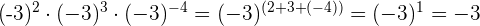
Das Ergebnis muss ein negatives Vorzeichen haben, da die Basis negativ und der Exponent eine ungerade Zahl ist:

Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

Da der Exponent negativ ist, müssen wir den Kehrwert der Basis mit positivem Exponent bilden:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Da der Exponent negativ ist, müssen wir den Kehrwert der Basis bilden:

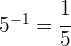
Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Da der Exponent negativ ist, müssen wir den Kehrwert der Basis mit positivem Exponent bilden:

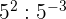
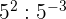
Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

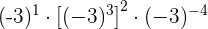
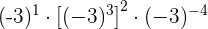
Um die Potenz einer Potenz zu berechnen, lassen wir die Basis stehen und multiplizieren die Exponenten miteinander:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Das Ergebnis muss ein negatives Vorzeichen haben, da die Basis negativ und der Exponent eine ungerade Zahl ist:

Vereinfache zuerst den Ausdruck in der Klammer. Lass dafür die Basis stehen und ziehe die Exponenten voneinander ab:

Um die Potenz einer Potenz zu berechnen, lassen wir die Basis stehen und multiplizieren die Exponenten miteinander:

Das Ergebnis muss ein negatives Vorzeichen haben, da die Basis negativ und der Exponent eine ungerade Zahl ist:

Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

Da die Potenz Exponent 1 hat, ist die Potenz gleich der Basis:

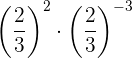
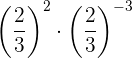
Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

Da der Exponent negativ ist, müssen wir den Kehrwert der Basis mit positivem Exponent bilden: Die Potenz, die wir erhalten, hat den Exponenten 1, d.h. die Potenz ist gleich der neuen Basis:

Um Potenzen mit derselben Basis zu multiplizieren, lassen wir die Basis stehen und summieren die Exponenten:

Da der Exponent negativ ist, müssen wir den Kehrwert der Basis mit positivem Exponent bilden:

Bilde beim zweiten Element den Kehrwert, um einen positiven Exponenten zu erhalten. Multipliziere dann Potenzen mit derselben Basis:

Da die Potenz Exponent 1 hat, ist die Potenz gleich der Basis:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Da der Exponent negativ ist, müssen wir den Kehrwert der Basis mit positivem Exponent bilden: Die Potenz, die wir erhalten, hat den Exponenten 1, d.h. die Potenz ist gleich der neuen Basis:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Da der Exponent negativ ist, müssen wir den Kehrwert der Basis mit positivem Exponent bilden:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Um Potenzen mit derselben Basis zu dividieren, lassen wir die Basis stehen und subtrahieren die Exponenten:

Die Potenz, die wir erhalten, hat den Exponenten 1, d.h. die Potenz ist gleich der neuen Basis:

Bilde beim ersten Element den Kehrwert, um einen positiven Exponenten zu erhalten. Multipliziere dann Potenzen mit derselben Basis:

Um die Potenz einer Potenz zu berechnen, lassen wir die Basis stehen und multiplizieren die Exponenten miteinander:

Um die Potenz einer Potenz zu berechnen, lassen wir die Basis stehen und multiplizieren die Exponenten miteinander:

Da der Exponent negativ ist, müssen wir den Kehrwert der Basis mit positivem Exponent bilden:

Stelle die Basen der Potenzen als Potenzen aus Primzahlen dar:

Bilde beim ersten Element den Kehrwert, um einen positiven Exponenten zu erhalten. Multipliziere dann Potenzen mit derselben Basis:

1 Bringe alle Brüche auf denselben Zähler und Nenner. Zerlege dafür die Zahlen, die keine Primzahlen sind, in ihre Faktoren:

2 Im Ausdruck sind Potenzen von Potenzen enthalten. Behalte ihre Basis bei und multipliziere ihre Exponenten:

3 Bilde für alle Potenzen mit Basis und negativem Exponenten den Kehrwert mit positivem Exponenten:

4 Multipliziere die Potenzen mit derselben Basis im Zähler sowie im Nenner des Bruchs. Dividiere dann die Ergebnisse. Bilde zum Schluss den Kehrbruch mit positivem Exponenten:

1 Führe zuerst die Multiplikationen und Divisionen innerhalb der Klammern durch:

2 Vereinfache die Brüche wo möglich, schreibe die gemischten Brüche um und berechne dann die Summen in den Klammern

3 Schreibe den hinteren Ausdruck um und wende das Potenzgesetzt für rationale Zahlen an:

4 Führe die Divisionen durch und vereinfache. Bilde zum Schluss die Subtraktion der übrigen Brüche:

Eine Potenz mit einem Bruch im Exponenten kann als Wurzel dargestellet werden: dabei kann die Basis des Exponenten als Radikant der Wurzel, der Nenner des Exponenten als Exponent des Radikanten und der Zähler des Exponenten als Wurzelexponent dargestellt werden. Zerlege die Zahl in ihre Faktoren, berechne den Radikant und ziehe die Wurzel:

Zerlege die Zahl in ihre Faktoren, berechne den Radikant und ziehe die Wurzel:

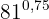
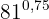
In diesem Fall ist der Exponent eine Dezimalzahl, die zuerst als Bruch umgeschrieben werden muss. Berechne dann den Radikant und ziehe die Wurzel:

Der Exponent ist eine Periodenzahl, die zuerst als Bruch umgeschrieben werden muss:

Bilde die Wurzel, berechne den Radikant und ziehe die Wurzel: