Primzahlen sind jene natürlichen Zahlen, die nur durch sich selbst und durch 1 teilbar sind, d.h. wenn man versucht, sie durch eine andere Zahl zu teilen, erhält man keine ganze Zahl als Ergebnis.
Einige Primzahlen sind
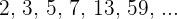
Die Zahl 1 hat nur einen Teiler, nämlich sich selbst, und gilt daher nicht als Primzahl.
Um zu beweisen, dass eine Zahl eine Primzahl ist, teilt man sie der Reihe nach durch alle Primzahlen, die kleiner als sie sind. Wenn wir ohne exakte Divisionen einen Quotienten erhalten, der kleiner oder gleich dem Divisor ist, können wir sagen, dass die betreffende Zahl eine Primzahl ist.
Beispiel: Ermittle, ob die Zahl 179 eine Primzahl ist.
Um festzustellen, ob 
eine Primzahl ist, muss man sie durch alle Primzahlen teilen, die kleiner sind als sie (in aufsteigender Reihenfolge), bis man einen Quotienten erhält, der kleiner oder gleich dem jeweiligen Divisor ist.
Wir beginnen mit der Division durch 
Für diesen Fall analysieren wir den folgenden Ausdruck
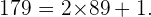
Wenn wir durch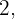 
teilen, erhalten wir als Quotienten die Zahl 
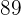und als Rest die Zahl 
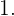Das bedeutet, dass die Division von durch 
keine ganze Zahl ergibt, da der Rest ungleich 0 ist.
Nun machen wir das Gleiche, aber mit den folgenden Primzahlen: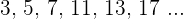 
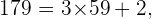
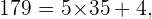
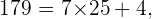
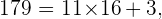
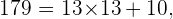
In diesem letzten Fall erhalten wir bei der Division von durch 
den Quotienten 
der kleiner ist als 
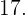Da diese Division auch einen Rest ungleich 0 ergibt, ist es gleichbedeutend mit der Aussage, dass sie keine ganze Zahl ergibt. Außerdem ist festzustellen, dass keine der Divisionen durch die anderen Primzahlen eine ganze Zahl ergeben hat.
Somit handelt es sich bei der Zahl um eine Primzahl.
Sieb des Eratosthenes
Das Sieb des Eratosthenes ist ein Algorithmus zum Ermitteln von Primzahlen, die kleiner sind als eine bestimmte natürliche Zahl.
Die Schritte eines solchen Algorithmus lauten wie folgt:
1 Wir gehen von einer Liste von Zahlen aus, die von bis zu einer bestimmten Zahl reicht.
2 Wir streichen die Vielfachen von von der Liste.
3 Wir nehmen die erste Zahl nach der , die nicht gestrichen wurde (die 
) und streichen ihre Vielfachen aus der Liste. Wir wiederholen den Vorgang immer wieder.
4 Der Vorgang endet, wenn das Quadrat der größten als Primzahl bestätigten Zahl kleiner ist als die letzte Zahl in der Liste.
Die Zahlen, die in der Liste verbleiben, sind also die Primzahlen.
Beispiel: Finde alle Primzahlen, die kleiner als 40 sind.
1 Zunächst schreiben wir alle Zahlen zwischen und 
auf.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
2 Nun streichen wir die Vielfachen von
| 2 | 3 | 5 | 7 | 9 | |
|---|---|---|---|---|---|
| 11 | 13 | 15 | 17 | 19 | |
| 21 | 23 | 25 | 27 | 29 | |
| 31 | 33 | 35 | 37 | 39 |
3 Die nächste Zahl ist 
und da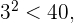 
streichen wir auch die Vielfachen von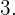 
| 2 | 3 | 5 | 7 | ||
|---|---|---|---|---|---|
| 11 | 13 | 15 | 17 | 19 | |
| 23 | 25 | 29 | |||
| 31 | 35 | 37 |
4 Die nächste Zahl ist 
und da 
streichen wir die Vielfachen von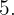 
| 2 | 3 | 5 | 7 | |||
|---|---|---|---|---|---|---|
| 11 | 13 | 17 | 19 | |||
| 23 | 29 | |||||
| 31 | 37 |
5 Und schließlich ist die nächste Zahl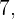 
jedoch ist 
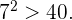Daher können wir den Algorithmus beenden und zu dem Schluss kommen, dass die übrigen Zahlen Primzahlen sein müssen.
| 2 | 3 | 5 | 7 | |||
|---|---|---|---|---|---|---|
| 11 | 13 | 17 | 19 | |||
| 23 | 29 | |||||
| 31 | 37 |
Tabelle der Primzahlen bis 1000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 |
|---|---|---|---|---|---|---|---|---|---|
| 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 | 113 |
| 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 |
| 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 | 229 |
| 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 |
| 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 |
| 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 | 541 |
| 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 | 601 |
| 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 | 733 |
| 739 | 743 | 751 | 757 | 761 | 769 | 773 | 787 | 797 | 809 |
| 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 | 863 |
| 877 | 881 | 883 | 887 | 907 | 911 | 919 | 929 | 937 | 941 |
| 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 | / | / |
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
