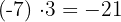Vorzeichenregel
Die Multiplikation zweier ganzer Zahlen entspricht dem Produkt der Faktoren und hat als Vorzeichen:
+ Wenn die Faktoren das gleiche Vorzeichen haben.
− Wenn das Vorzeichen der Faktoren unterschiedlich ist.
Allgemein lässt sich sagen, dass die Multiplikation mehrerer ganzer Zahlen eine weitere ganze Zahl ergibt, deren Wert dem Produkt der Beträge entspricht und deren Vorzeichen sich aus der Anwendung der Vorzeichenregel ergibt.
+ · + = +
− · − = +
+ · − = −
− · + = −
Beispiel:
Eigenschaften der Multiplikation
1 Intern
Das Ergebnis der Multiplikation zweier ganzer Zahlen ist eine weitere ganze Zahl.
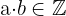
Beispiel:
2Assoziativ
Die Art und Weise, wie die Faktoren angeordnet werden, hat keinen Einfluss auf das Ergebnis. Wenn a, b und c beliebige ganze Zahlen sind, gilt:
Beispiel:
3Kommutativ
Die Reihenfolge der Faktoren ändert nichts am Ergebnis.
Beispiel:
4Neutrales Element
Die 1 ist das neutrale Element der Multiplikation, da jede Zahl, die mit ihr multipliziert wird, dieselbe Zahl ergibt.
Beispiel:
5Distributiv
Das Produkt einer Zahl und einer Summe ist gleich der Summe der Produkte dieser Zahl und jedem der Summanden.
Beispiel:
6 Gemeinsamen Faktor ausklammern
Es ist der umgekehrte Prozess zum Distributivgesetz.
Wenn mehrere Summanden einen gemeinsamen Faktor haben, können wir die Summe in ein Produkt umwandeln, indem wir diesen Faktor ausklammern.
Beispiel:
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
