Kapitel
Eine rationale Zahl ist jede Zahl, die sich als Quotient zweier ganzer Zahlen mit einem Nenner ungleich null darstellen lässt. Sie wird mit 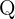 dargestellt.
dargestellt.
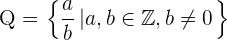
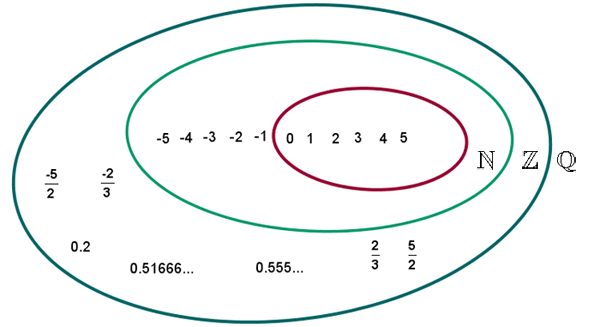

Addition und Subtraktion von rationalen Zahlen
Die Addition (Subtraktion) von rationalen Zahlen erfolgt je nach ihrem Nenner: ob sie denselben oder einen unterschiedlichen Nenner haben.
Gleicher Nenner
Die Zähler werden addiert oder subtrahiert, der Nenner bleibt gleich.
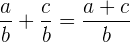

Beispiele:
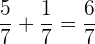

Unterschiedlicher Nenner
Zunächst werden die Nenner auf einen gemeinsamen Nenner gebracht und die Zähler der erhaltenen äquivalenten Brüche werden addiert oder subtrahiert.

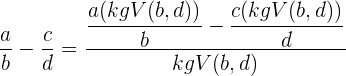
Beispiele:
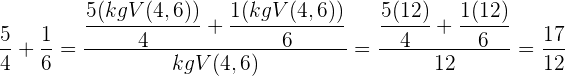
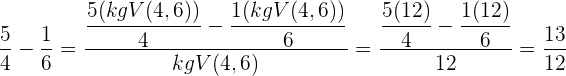
Regeln für die Addition von rationalen Zahlen
Für jedes 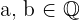 gelten folgende Regeln:
gelten folgende Regeln:
1 Die Summe von rationalen Zahlen ergibt wiederum eine rationale Zahl.

2 Assoziativ. Die Addition der ersten beiden Zahlen und die Addition einer dritten Zahl zu diesem Ergebnis ist dasselbe wie die Addition des Ergebnisses der Addition der zweiten und dritten Zahl zur ersten Zahl.
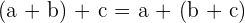
Beispiel:
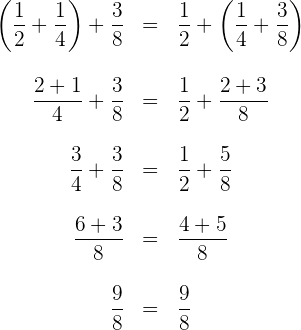
3 Kommutativ. Wenn die Summanden vertauscht werden, bleibt das Ergebnis dasselbe
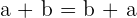
Beispiel:

4 Neutrales Element. Es gibt ein Element 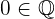 , so dass das Ergebnis bei der Addition mit einer Zahl immer noch dieselbe Zahl ist
, so dass das Ergebnis bei der Addition mit einer Zahl immer noch dieselbe Zahl ist
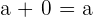
Beispiel:
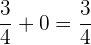
5 Gegenzahl. Jede rationale Zahl hat eine Gegenzahl, so dass das Ergebnis, wenn beide addiert werden, das neutrale Element ergibt.
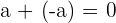
Beispiel:

Die Gegenzahl der Gegenzahl einer Zahl ist gleich der gleichen Zahl.
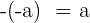
Multiplikation von rationalen Zahlen
Das Ergebnis der Multiplikation zweier rationaler Zahlen ergibt wiederum eine rationale Zahl, deren Zähler durch Multiplikation der Zähler und deren Nenner durch Multiplikation der Nenner erhalten wird
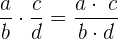
Beispiel:
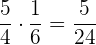
Regeln für die Multiplikation von rationalen Zahlen
Für jedes 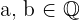 gelten folgende Regeln:
gelten folgende Regeln:
1 Interna. Die Multiplikation zweier rationaler Zahlen ergibt eine rationale Zahl
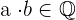
2 Assoziativ. Die Multiplikation der ersten beiden Zahlen und die Multiplikation des Ergebnisses mit einer dritten Zahl ist dasselbe wie die Multiplikation der ersten Zahl mit dem Ergebnis der Multiplikation der zweiten Zahl mit der dritten Zahl

Beispiel:

3 Kommutativ. Das Ergebnis einer Multiplikation bleibt durch Vertauschen der Multiplikanden unverändert
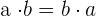
Beispiel:
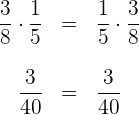
4Neutrales Element. Es gibt ein Element 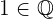 , bei dem das Ergebnis nach der Multiplikation mit einer Zahl immer noch dieselbe Zahl ist
, bei dem das Ergebnis nach der Multiplikation mit einer Zahl immer noch dieselbe Zahl ist
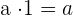
Beispiel:

5Inverses Element. Jede rationale Zahl ungleich null hat eine Gegenzahl, so dass bei der Multiplikation der beiden Zahlen das Ergebnis das neutrale Element der Multiplikation ist

Beispiel:

6 Distributiv
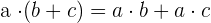
Beispiel:
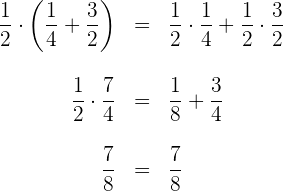
7 Den gemeinsamen Faktor ausklammern.

Beispiel:
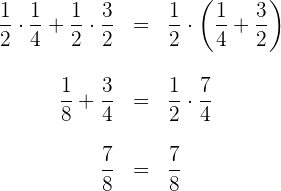
Division rationaler Zahlen
Das Ergebnis der Division von zwei rationalen Zahlen ist wiederum eine rationale Zahl, deren Zähler durch Multiplikation der äußerden Werte und deren Nenner durch Multiplikation der mittleren Werte erhalten wird
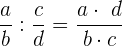
Beispiel:
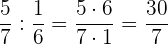
Potenzen von rationalen Zahlen
Potenzen von ganzzahligen Exponenten und rationaler Basis
Sie besteht darin, den Zähler und den Nenner auf die gegebene Potenz zu erhöhen. Ist die Potenz negativ, so ist das Ergebnis der Kehrwert der Basis, der mit der positiven Potenz erhöht wird, d. h. für 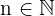

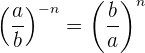
Beispiele:


Regeln
1 Jede rationale Zahl ungleich null, die zur Potenz Null erhoben wird, ergibt 1.
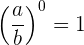
2 Jede rationale Zahl, die zur Potenz 1 erhoben wird, ergibt die gleiche rationale Zahl

3 Produkt von Potenzen mit gleicher Basis. Die Basis bleibt gleich und die Exponenten werden addiert
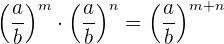
Beispiel:
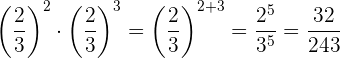
4 Division von Potenzen mit gleicher Basis. Die Basis bleibt gleich und die Exponenten werden subtrahiert
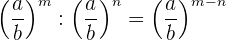
Beispiel:

5 Potenz einer Potenz. Die Basis bleibt gleich und die Exponenten werden multipliziert

Beispiel:
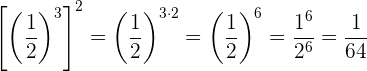
6 Produkt aus Potenzen mit dem gleichen Exponenten. Der Exponent bleibt gleich und die Basen werden multipliziert

Beispiel:
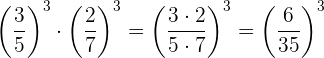
7 Quotient von Potenzen mit gleichem Exponenten. Der Exponent bleibt gleich und die Basen werden dividiert

Beispiel:
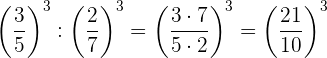
Aufgaben mit Lösungen

1 Wir lösen die Klammern auf

2 Wir nehmen das 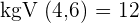 und wenden die Addition von Brüchen mit unterschiedlichem Nenner an
und wenden die Addition von Brüchen mit unterschiedlichem Nenner an


1 Wir führen die Addition in der Klammer durch und nehmen das 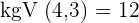
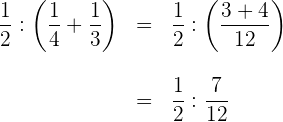
2 Wir dividieren die Brüche und vereinfachen das Ergebnis
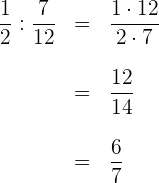

1 Wir subtrahieren innerhalb der Klammern
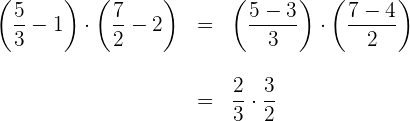
2 Wir multiplizieren die Brüche und vereinfachen das Ergebnis


1 Wir addieren innerhalb der Klammer

2 Wir dividieren die Brüche und vereinfachen das Ergebnis
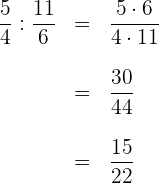
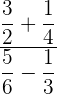
1 Wir führen die Additionen und Subtraktionen im Nenner und Zähler durch
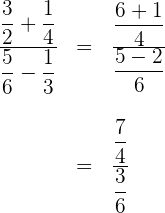
2 Wir schreiben in Divisionsschreibweise und führen die Rechenoperation durch. Schließlich wird das Ergebnis vereinfacht

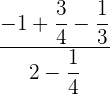
1 Wir führen die Additionen und Subtraktionen im Nenner und Zähler durch

2 Wir schreiben in Divisionsschreibweise und führen die Rechenoperation durch. Schließlich wird das Ergebnis vereinfacht


Da wir Potenzen mit der gleichen Basis multiplizieren, bleibt die Basis gleich und wir addieren die Exponenten


Da wir Potenzen mit der gleichen Basis multiplizieren, behalten wir die Basis bei und addieren die Exponenten

Da die resultierende Potenz den Exponenten 1 hat, ist die Potenz gleich der Basis

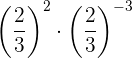
Da wir Potenzen mit der gleichen Basis multiplizieren, behalten wir die Basis bei und addieren die Exponenten

CDa die resultierende Potenz einen negativen Exponenten hat, ist die Potenz gleich dem Kehrwert der Basis mit positivem Exponenten. Schließlich hat die resultierende Potenz den Exponenten 1, so dass die Potenz gleich der neuen Basis ist
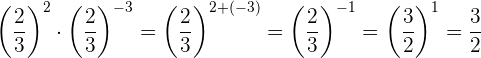

Da wir Potenzen mit der gleichen Basis multiplizieren, behalten wir die Basis bei und addieren die Exponenten

Da die resultierende Potenz einen negativen Exponenten hat, ist die Potenz gleich dem Kehrwert der Basis mit einem positiven Exponenten.
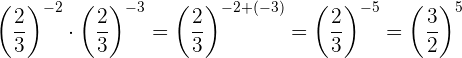

Wir ändern das 2. Element in einen positiven Exponenten. Hierfür ändert sich die Basis in ihren Kehrwert und wir führen die Multiplikation von Potenzen mit der gleichen Basis durch

Die sich daraus ergebende Potenz hat den Exponenten 1, sodass die Potenz gleich der Basis ist


Da wir Potenzen mit der gleichen Basis dividieren, bleibt die Basis gleich und wir subtrahieren die Exponenten

Da die resultierende Potenz einen negativen Exponenten hat, ist die Potenz gleich dem Kehrwert der Basis mit positivem Exponenten. Da die resultierende Potenz den Exponenten 1 hat, ist die Potenz schließlich gleich der neuen Basis

Da wir Potenzen mit der gleichen Basis dividieren, bleibt die Basis gleich und wir subtrahieren die Exponenten

Da die resultierende Potenz einen negativen Exponenten hat, ist die Potenz gleich dem Kehrwert der Basis mit einem positiven Exponenten


Da wir Potenzen mit der gleichen Basis dividieren, bleibt die Basis gleich und wir subtrahieren die Exponenten


Da wir Potenzen mit der gleichen Basis dividieren, bleibt die Basis gleich und wir subtrahieren die Exponenten

Da die resultierende Potenz den Exponenten 1 hat, ist die Potenz gleich der neuen Basis


Wir ändern das erste Element in einen positiven Exponenten. Hierfür ändert sich die Basis in ihren Kehrwert und wir führen die Division von Potenzen mit der gleichen Basis durch


Da es sich um eine Potenz einer Potenz handelt, bleibt die Basis gleich und wir multiplizieren die Exponenten


Da es sich um eine Potenz einer Potenz handelt, bleibt die Basis gleich und wir multiplizieren die Exponenten

Da die resultierende Potenz einen negativen Exponenten hat, ist die Potenz gleich dem Kehrwert der Basis mit einem positiven Exponenten.


1 Wir drücken die Basen der Potenzen als Potenzen von Primzahlen aus

2 Wir ändern das erste Element in einen positiven Exponenten. Hierfür ändert sich die Basis in ihren Kehrwert und wir führen die Division von Potenzen mit der gleichen Basis durch


1 Wir schreiben alle Brüche mit gleichem Zähler und gleichem Nenner zusammen und zerlegen dazu die Zahlen, die keine Primzahlen sind, in Faktoren.

2 Es gibt Elemente, die Potenzen von Potenzen sind, sodass die Basis erhalten bleibt und die Exponenten multipliziert werden

3 Für Potenzen mit der Basis  und negativen Exponenten wird der umgekehrte Bruch mit positivem Exponenten verwendet
und negativen Exponenten wird der umgekehrte Bruch mit positivem Exponenten verwendet

4 Sowohl im Zähler als auch im Nenner multiplizieren wir die Potenzen mit der gleichen Basis und dividieren die Ergebnisse. Schließlich schreiben wir den Kehrbruch mit positivem Exponenten


1 Zunächst arbeiten wir mit den Produkten und gemischten Zahlen in den Klammern.

2 Wir berechnen die Summen innerhalb der Klammern und vereinfachen die 3. Klammer
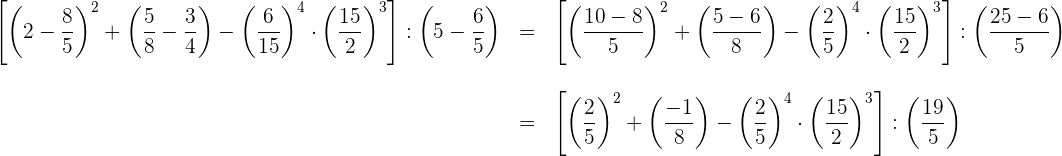
3 Wir führen die Multiplikationen durch und vereinfachen den 3. Bruch
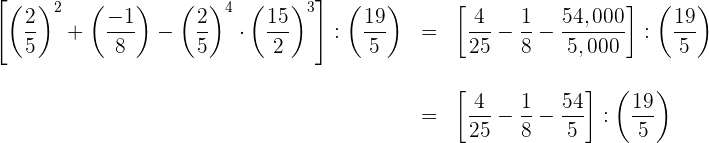
4 Wir addieren und stellen fest, dass das 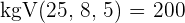 ist
ist

5 Wir dividieren und vereinfachen


1 Erstens: Wegen der einzuhaltenden Reihenfolge der Rechenoperationen führen wir die Multiplikationen und Divisionen innerhalb der Klammern durch.

2 Wir vereinfachen die Brüche, wo dies möglich ist, schreiben die gemischten Brüche um und berechnen dann die Summe in den Klammern

3 Wir schreiben den letzten Ausdruck um und wenden die Regeln für die Potenzen rationaler Zahlen an

4 Wir führen die Divisionen durch und vereinfachen. Schließlich subtrahieren wir die resultierenden Brüche


1 Wir vereinfachen die Brüche, wo es möglich ist, und fahren mit der Addition und Subtraktion innerhalb der Klammern fort
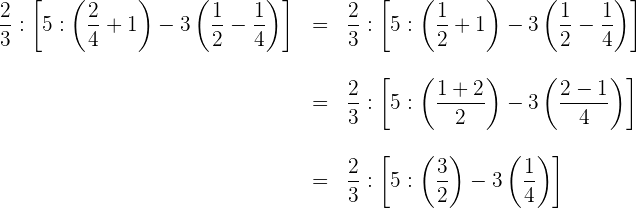
2 Wir führen die Multiplikationen und Divisionen innerhalb der eckigen Klammern durch
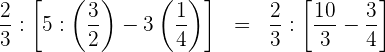
3 Wir subtrahieren innerhalb der eckigen Klammer
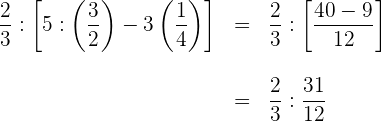
4 Schließlich führen wir die Division durch und vereinfachen das Ergebnis

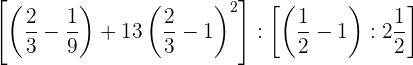
1 Wir führen die Berechnungen in den Klammern durch und schreiben den gemischten Bruch um
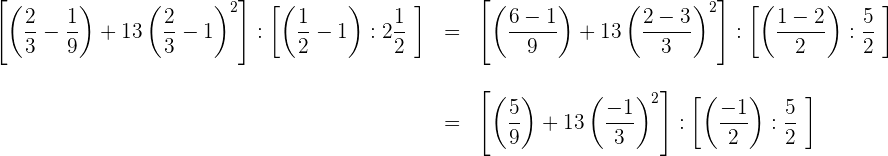
2 Wir führen die Multiplikationen, Divisionen und Potenzen innerhalb der eckigen Klammern aus
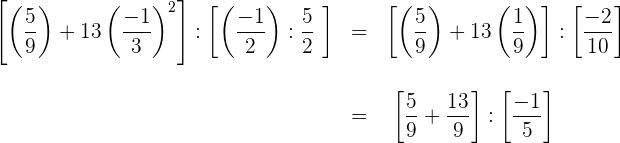
3 Wir führen die Addition in der eckigen Klammer durch
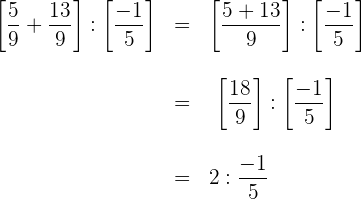
4 Und schließlich dividieren wir
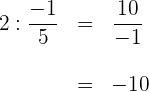
Mit KI zusammenfassen:













