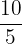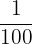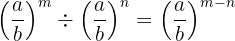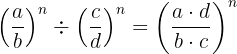Kapitel
Definition der rationalen Zahlen
Eine rationale Zahl ist jede Zahl, die als Quotient zweier ganzer Zahlen mit einem Nenner ungleich 0 dargestellt werden kann. Mit anderen Worten, eine rationale Zahl hat die Form
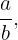
wobei 
und 
sind ganze Zahlen.
Beispiel
- Jede ganze Zahl ist rational, denn wenn eine ganze Zahl ist, können wir sie als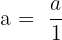
ausdrücken. Zum Beispiel ist 
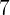rational, da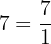 
Darstellung der rationalen Zahlen
Die rationalen Zahlen werden auf der Geraden neben den ganzen Zahlen dargestellt.
1 Nehmen wir beispielsweise ein Segment der Länge 1.
2 Wir zeichnen ein Hilfssegment vom Ursprung aus und teilen es in die gewünschten Teile auf. In unserem Beispiel teilen wir es in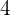 
Teile.
3 Wir verbinden den letzten Punkt des Hilfssegments mit dem Ende des anderen Segments und zeichnen parallele Segmente an jedem der Punkte, die wir durch die Teilung des Hilfssegments erhalten haben.
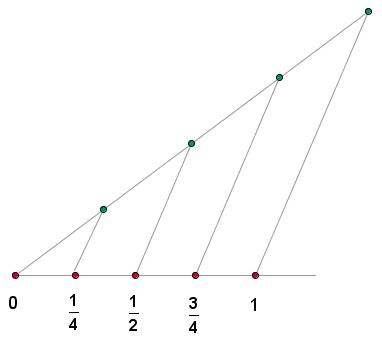
In der Praxis werden rationale Zahlen und Brüche synonym verwendet.
Rechenoperationen mit rationalen Zahlen
Die arithmetischen Operationen mit rationalen Zahlen sind wie folgt definiert
1. Addition von Brüchen
Gegeben sind zwei Brüche 
und 
. Wir definieren die Summe als
.
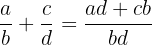Wenn der Nenner bei beiden Brüchen Gleich ist, nämlich und 
, können wir einfacher addieren
.
Beispiele
.
.
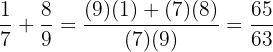2. Subtraktion von Brüchen
Gegeben sind zwei Brüche und . Wir definieren ihre Differenz als
.
Wenn der Nenner bei beiden Brüchen gleich ist, nämlich und , können wir einfacher subtrahieren
.
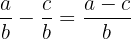Beispiele
.
.
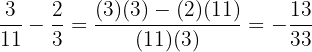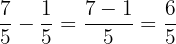3. Multiplikation von Brüchen
Gegeben sind zwei Brüche und . Wir definieren ihr Produkt als
.
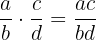Beispiel
.
.
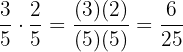4. Division von Brüchen
Gegeben sind zwei Brüche und . Wir definieren ihre Division als
.
Beispiel
.
.
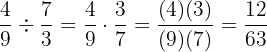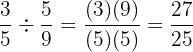Eigenschaften der rationalen Zahlen
Die rationalen Zahlen haben einige Eigenschaften, zum Beispiel
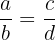, wenn (und nur wenn) gilt, dass 
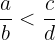, wenn (und nur wenn) gilt, dass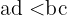 
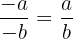
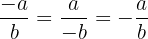
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
