Alicia gibt  € für Einkäufe aus. Am Donnerstag gibt sie
€ für Einkäufe aus. Am Donnerstag gibt sie  dieses Betrags aus und am Samstag
dieses Betrags aus und am Samstag  von dem, was dann noch bleibt. Wie viel gibt sie pro Tag aus und wie viel bleibt am Ende übrig?
von dem, was dann noch bleibt. Wie viel gibt sie pro Tag aus und wie viel bleibt am Ende übrig?
Ausgaben am Donnerstag 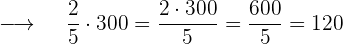 €
€
Verbleibender Betrag  €
€
Ausgaben am Samstat 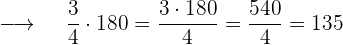 €
€
Am Schluss verbleibender Betrag  €
€
Von den Einkünften einer Anwohnervereinigung werden folgende Beträge verwendet:
 für Heizung
für Heizung für Strom
für Strom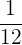 für die Müllabfuhr
für die Müllabfuhr für die Instandhaltung des Gebäudes
für die Instandhaltung des Gebäudes
und der Rest wird für die Reinigung ausgegeben.
Welcher Anteil der Einnahmen wird für die Reinigung ausgegeben?
Ordne die aufgelisteten Posten entsprechend dem verwendeten Einkommensanteil vom kleinsten zum größten Posten.
1 Finde einen Ausdruck, der die Daten in Beziehung setzt und berechne
 sei der Bruch, der für den Betrag steht, der für die Reinigung ausgegeben wird
sei der Bruch, der für den Betrag steht, der für die Reinigung ausgegeben wird
Da das gesamte Geld ausgegeben wird, müssen die Anteile der einzelnen Ausgaben  ergeben.
ergeben.
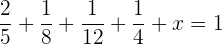
Wir suchen nach dem kleinsten gemeinsamen Vielfachen der Nenner
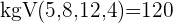
Gleiche Brüche erhält man, indem man das kgV durch den Nenner dividiert, die resultierende Zahl mit dem Zähler multipliziert und das kgV in den Nenner einsetzt.
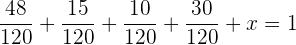
Wir addieren die Brüche


Wir bestimmen 
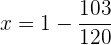
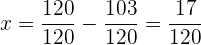
Schließlich werden 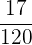 für die Reinigung ausgegeben
für die Reinigung ausgegeben
2 Ordne die Brüche
Um die Brüche zu ordnen, müssen wir sie auf einen gemeinsamen Nenner bringen, was wir bereits mit der Addition getan haben
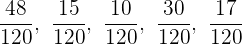
Wir können sie wie folgt ordnen
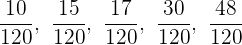
Wir vereinfachen zu den ursprünglichen Brüchen, die wir hatten
 \displaystyle \frac{1}{12}<\frac{1}{8}<\frac{17}{120}< \frac{1}{4}< \frac{2}{5}[/latex]
\displaystyle \frac{1}{12}<\frac{1}{8}<\frac{17}{120}< \frac{1}{4}< \frac{2}{5}[/latex]
Führe folgende Berechnungen durch:
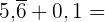
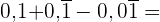
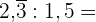
In dieser Übung haben wir Summen von exakten, rein perodischen und gemischten Dezimalzahlen, die wir in ihre jeweiligen Brüche umwandeln werden.
Wenn der Bruch eine exakte Dezimalzahl ist, ist der Zähler des Bruchs die angegebene Zahl ohne Dezimalpunkt und der Nenner die Einheit, gefolgt von so vielen Nullen, wie es Dezimalstellen gibt.
Ist der Bruch eine rein periodische Zahl, so hat der sich ergebende Bruch als Zähler die angegebene Zahl ohne Komma, abzüglich des ganzzahligen Teils, und als Nenner eine Zahl, die aus so vielen Neunen gebildet wird, wie die Periode Ziffern hat.
Ist der Bruch eine gemischte periodische Zahl, so hat der sich ergebende Bruch als Zähler die angegebene Zahl ohne Komma, abzüglich des ganzzahligen Teils, gefolgt von den nichtperiodischen Dezimalziffern, und als Nenner eine Zahl, die aus so vielen Neunen gebildet wird, wie die Periode Ziffern hat, gefolgt von so vielen Nullen, wie der nichtperiodische Dezimalteil Ziffern hat.
Somit:
1 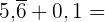
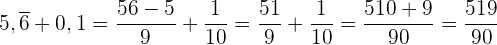
2 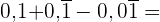
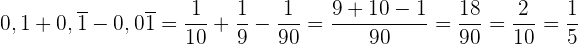
3 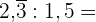
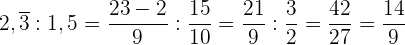
Berechne:
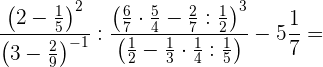
Wir führen die in Klammern angegebenen Berechnungen durch. In der Klammer des zweiten Nenners müssen wir zuerst multiplizieren und im nächsten Schritt dividieren.
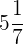 ist eine gemischte Zahl. Wir behalten also den Nenner
ist eine gemischte Zahl. Wir behalten also den Nenner  bei. Der Zähler ist die Summe der Multiplikation aus
bei. Der Zähler ist die Summe der Multiplikation aus  und dem Nenner
und dem Nenner  plus dem Zähler der Zahl
plus dem Zähler der Zahl  .
.
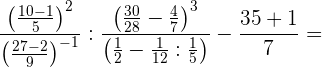
Wir führen die angegebenen Berechnungen durch und vereinfachen 
Wir führen die angegebenen Rechenschritte durch und bringen den zweiten Bruch auf einen gemeinsamen Nenner

Wir führen die Rechenoperationen für den zweiten Bruch aus und vereinfachen

Wir führen die Potenzen durch und bedenken, dass wir bei einem Bruch, der auf eine negative Zahl erhöht ist, den Zähler in den Nenner umwandeln und dann auf den Exponenten erhöhen müssen.
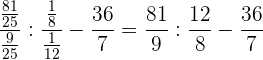
Im vorangegangenen Schritt haben wir Folgendes berücksichtigt:
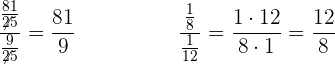
Wir vereinfachen und berechnen.
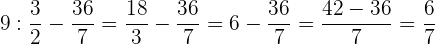
Berechne:
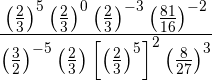
Wir werden versuchen, alle Brüche mit demselben Zähler und Nenner zu bilden, indem wir die Zahlen, die keine Primzahlen sind, in Faktoren zerlegen.

Wir wenden das Gesetz der Exponenten an. Da es sich um eine Potenz einer Potenz eines Bruches handelt, werden die Exponenten multipliziert
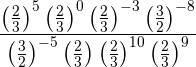
Um eine Potenz mit negativem Exponenten in einen positiven Exponenten umzuwandeln, müssen wir die Umkehrung des Bruches vornehmen
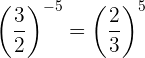

Und somit
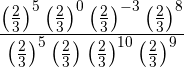
Sowohl im Zähler als auch im Nenner werden die Potenzen mit der gleichen Basis multipliziert und die Ergebnisse dividiert
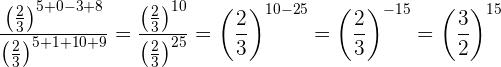
Mit KI zusammenfassen:


