Kapitel
Die statistische Inferenz befasst sich mit Methoden, die es ermöglichen, aus der Analyse einer Stichprobe allgemeine Schlussfolgerungen über eine Grundgesamtheit zu ziehen. Darüber hinaus wird der Grad der Zuverlässigkeit oder Konfidenz der erzielten Ergebnisse untersucht. Im Folgenden geben wir dir einen Überblick über die gängigsten Methoden der statistischen Inferenz.

Arten von Stichproben
Eine Stichprobe besteht aus einer Teilmenge einer Grundgesamtheit. Die Stichprobe wird mit  gekennzeichnet und die Grundgesamtheit mit
gekennzeichnet und die Grundgesamtheit mit  . Es werden folgende Arten der Stichprobe unterschieden:
. Es werden folgende Arten der Stichprobe unterschieden:
Einfache Zufallsstichprobe
Bei einer Zufallsstichprobe werden alle Elemente der Grundgesamtheit aufgezählt. Dann werden  Elemente zufällig aus der Grundgesamtheit ausgewählt..
Elemente zufällig aus der Grundgesamtheit ausgewählt..
1 Wenn nach der Auswahl eines Elements  dieses nicht erneut ausgewählt werden kann, wird die Stichprobe als Stichprobe ohne Wiederholung bezeichnet.
dieses nicht erneut ausgewählt werden kann, wird die Stichprobe als Stichprobe ohne Wiederholung bezeichnet.
2 Kann dagegen das Element  mehr als einmal ausgewählt werden, so spricht man von einer Stichprobe mit Wiederholung.
mehr als einmal ausgewählt werden, so spricht man von einer Stichprobe mit Wiederholung.
Systematische Zufallsstichprobe
Bei der systematischen Stichprobe wird ein zufälliger Ausgangspunkt  gewählt. Davon ausgehend werden die anderen Elemente in gleichmäßigen Intervallen entnommen, bis die Stichprobe vollständig ist. Das heißt:
gewählt. Davon ausgehend werden die anderen Elemente in gleichmäßigen Intervallen entnommen, bis die Stichprobe vollständig ist. Das heißt:  , wobei
, wobei  zufällig ist.
zufällig ist.
Geschichtete Zufallsstichprobe
Bei geschichteten Zufallsstichproben wird die Grundgesamtheit natürlich in verschiedene Klassen oder Schichten unterteilt (diese müssen sich gegenseitig ausschließen); dann wird für jede der Schichten eine einfache Zufallsstichprobe gezogen.
Wenn der Umfang der einzelnen Teilgesamtheiten proportional zum Umfang der Schicht im Verhältnis zur Grundgesamtheit ist, dann handelt es sich um eine geschichtete Stichprobe mit proportionaler Zuordnung.
Cluster-Stichprobe
Auch hier wird die Grundgesamtheit in Klassen unterteilt (die sich jedoch nicht unbedingt gegenseitig ausschließen). Bei Cluster-Stichproben werden eher Klassen als einzelne Elemente untersucht.
Anstatt beispielsweise alle Studierenden einer Universität zu betrachten, nehmen wir eine Stichprobe von Unterrichtsräumen: So werden alle Studierenden in diesen Räumen befragt und die Stichprobe wird vereinfacht.
Verteilung der Stichprobenmittelwerte
Der zentrale Grenzwertsatz gibt Aufschluss über die Verteilung des Mittelwerts einer Stichprobe. Dies ist für statistische Inferenzen sehr wichtig.
Zentraler Grenzwertsatz
Zentraler Grenzwertsatz.  sei eine Grundgesamtheit mit dem Mittelwert
sei eine Grundgesamtheit mit dem Mittelwert  und der Standardabweichung
und der Standardabweichung  . Wenn wir eine Stichprobe vom Umfang
. Wenn wir eine Stichprobe vom Umfang  nehmen, nähern sich die Mittelwerte
nehmen, nähern sich die Mittelwerte 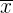 dieser Stichproben einer Normalverteilung mit dem Mittelwert
dieser Stichproben einer Normalverteilung mit dem Mittelwert  und der Standardabweichung
und der Standardabweichung  . Das heißt:
. Das heißt:
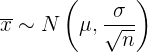
Die Bedingung, dass 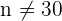 , ist nicht notwendig, wenn die ursprüngliche Grundgesamtheit
, ist nicht notwendig, wenn die ursprüngliche Grundgesamtheit  einer Normalverteilung folgt.
einer Normalverteilung folgt.
Folgen des zentralen Grenzwertsatzes
Die folgenden Punkte sind wichtige Folgen des zentralen Grenzwertsatzes:
1 Er ermöglicht es, die Wahrscheinlichkeit zu bestimmen, dass der Mittelwert einer bestimmten Stichprobe innerhalb eines bestimmten Intervalls liegt.
2 Mit ihm lässt sich die Wahrscheinlichkeit berechnen, dass die Summe der Elemente einer Stichprobe grundsätzlich in einem bestimmten Intervall liegt. Dies folgt aus
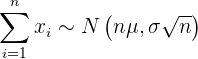
3 Er hilft uns, von einer Stichprobe auf den Mittelwert der Grundgesamtheit zu schließen.
Schätzung von Stichprobenparametern
Es gibt zwei Möglichkeiten, einen Parameter oder eine Eigenschaft einer Grundgesamtheit zu schätzen: Punktschätzung und Intervallschätzung.
Punktschätzung
Die Punktschätzung erfolgt durch Berechnung einer einzigen Zahl, der Parameterschätzung. Bei einer Stichprobe  wird also eine Zahl
wird also eine Zahl  berechnet und als Wert des Parameters der Grundgesamtheit angenommen.
berechnet und als Wert des Parameters der Grundgesamtheit angenommen.
Es gibt folgende Punktschätzungen:
1 Der Mittelwert  einer Grundgesamtheit mit Normalverteilung wird mit dem Durchschnittswert geschätzt
einer Grundgesamtheit mit Normalverteilung wird mit dem Durchschnittswert geschätzt
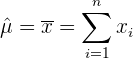
2 Die Standardabweichung  einer Grundgesamtheit mit Normalverteilung wird anhand der Stichprobenabweichung geschätzt
einer Grundgesamtheit mit Normalverteilung wird anhand der Stichprobenabweichung geschätzt
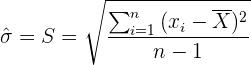
3 Der Anteil  einer Grundgesamtheit mit Binomialverteilung ergibt sich aus dem Stichprobenanteil
einer Grundgesamtheit mit Binomialverteilung ergibt sich aus dem Stichprobenanteil
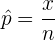 ,
,
wobei  die Anzahlder Elemente in
die Anzahlder Elemente in  ist, die die gewünschte Eigenschaft erfüllen.
ist, die die gewünschte Eigenschaft erfüllen.
Konfidenzintervalle
Ein Konfidenzintervall 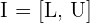 ist ein Intervall, bei dem wir wissen, dass der Parameter mit einem bestimmten Konfidenzniveau in diesem liegt.
ist ein Intervall, bei dem wir wissen, dass der Parameter mit einem bestimmten Konfidenzniveau in diesem liegt.
Das Konfidenzniveau bezieht sich auf die Wahrscheinlichkeit, dass der zu schätzende Parameter innerhalb unseres Konfidenzintervalls liegt. Es wird in der Regel mit  angegeben.
angegeben.
Der zulässige Schätzungsfehler bezieht sich auf die zulässige Fehlerwahrscheinlichkeit. Diese wird mit  bezeichnet.
bezeichnet.
Der kritische Wert der Normalverteilung wird mit  angegeben. Für den kritischen Wert gilt:
angegeben. Für den kritischen Wert gilt:
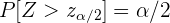
und somit auch
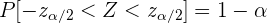
Charakteristische Intervalle
Für die Normalverteilung 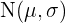 haben die Konfidenzintervalle die Form
haben die Konfidenzintervalle die Form

Die folgende Tabelle zeigt die charakteristischen Intervalle für die häufigsten  Signifikanzwerte:
Signifikanzwerte:
 | 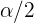 |  | Charakteristische Intervalle |
|---|---|---|---|
| 0,90 | 0,05 | 1,645 | 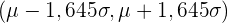 |
| 0,95 | 0,025 | 1,96 | 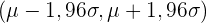 |
| 0,99 | 0,005 | 2,575 | 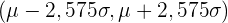 |
Schätzung des Mittelwerts mit Konfidenzintervall
Um den Mittelwert einer Grundgesamtheit  anhand der Stichprobe
anhand der Stichprobe  zu schätzen, wird das folgende Konfidenzintervall verwendet
zu schätzen, wird das folgende Konfidenzintervall verwendet
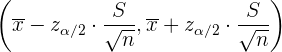 ,
,
wobei 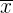 der Durchschnittswert von
der Durchschnittswert von  ,
,  die Standardabweichung von
die Standardabweichung von  und
und  der Umfang von
der Umfang von  ist. Außerdem ist
ist. Außerdem ist  das gewünschte Konfidenzniveau.
das gewünschte Konfidenzniveau.
In diesem Fall ist der maximale Schätzungsfehler
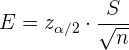 .
.
Darüber hinaus wird der Stichprobenumfang, der für eine gewünschte Genauigkeit erforderlich ist, wie folgt berechnet

Um den erforderlichen Stichprobenumfang zu berechnen, müssen wir die Standardabweichung der Grundgesamtheit kennen. Diese kann mit einer kleinen Stichprobe geschätzt werden, und dann kann eine zweite Stichprobe mit dem erforderlichen Stichprobenumfang durchgeführt werden.
Verhältnisschätzung mit Konfidenzintervall
Angenommen, wir haben eine Grundgesamtheit  , bei der ein Anteil
, bei der ein Anteil  dieser Grundgesamtheit ein bestimmtes Merkmal erfüllt. Somit folgt der Anteil der Elemente
dieser Grundgesamtheit ein bestimmtes Merkmal erfüllt. Somit folgt der Anteil der Elemente  , die diese Eigenschaft bei einem Stichprobenumfang von
, die diese Eigenschaft bei einem Stichprobenumfang von  erfüllen, näherungsweise einer Normalverteilung:
erfüllen, näherungsweise einer Normalverteilung:

Daraus folgt, dass die Schätzung des Anteils  aus dem Anteil von
aus dem Anteil von  in einer Stichprobe durch das folgende Intervall erfolgt:
in einer Stichprobe durch das folgende Intervall erfolgt:
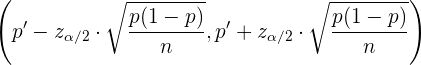
Der maximale Schätzungsfehler ist hier gegeben durch

Statistische Hypothesen und Arten von Tests
Ein statistischer Test ist ein Verfahren, mit dem aus einer Stichprobe auf die Gültigkeit einer Hypothese über einen bestimmten Parameter der Grundgesamtheit geschlossen werden kann.
Die Hypothese, die für die Grundgesamtheit gilt, wird mit  angegeben und als Nullhypothese bezeichnet. Die Nullhypothese muss immer die Form „ist gleich“, „ist kleiner als oder gleich“ oder „ist größer als oder gleich“ haben.
angegeben und als Nullhypothese bezeichnet. Die Nullhypothese muss immer die Form „ist gleich“, „ist kleiner als oder gleich“ oder „ist größer als oder gleich“ haben.
Die Gegenhypothese zur Hypothese der Grundgesamtheit wird mit  angegeben und ist die Alternativhypothese. Diese Hypothese hat die Form „ist anders als“, „ist größer als“ oder „ist kleiner als“.
angegeben und ist die Alternativhypothese. Diese Hypothese hat die Form „ist anders als“, „ist größer als“ oder „ist kleiner als“.
Schritte zur Durchführung eines Hypothesentests
Das Verfahren zur Durchführung eines Hypothesentests (für den Mittelwert 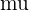 oder das Verhältnis
oder das Verhältnis  ) ist im Allgemeinen wie folgt:
) ist im Allgemeinen wie folgt:
1 Die Nullhypothese  und die Alternativhypothese
und die Alternativhypothese  werden angegeben.
werden angegeben.
2 Es wird das Konfidenzniveau  oder das Signifikanzniveau
oder das Signifikanzniveau  bestimmt.
bestimmt.
3 Damit wird der Wert  (für den zweiseitigen Test) oder
(für den zweiseitigen Test) oder 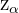 (für den einseitigen Test) berechnet.
(für den einseitigen Test) berechnet.
4 Dann wird der Akzeptanzbereich des Stichprobenparameters konstruiert (weitere Einzelheiten im nächsten Abschnitt).
5 Aus der Grundgesamtheit wird eine Stichprobe mit  gezogen, so dass die Normalverteilung angewendet werden kann.
gezogen, so dass die Normalverteilung angewendet werden kann.
6 Anhand der Stichlprobe wird 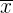 oder
oder  berechnet.
berechnet.
7 Liegt der Wert des Stichprobenparameters innerhalb des Akzeptanzbereichs, so wird die Nullhypothese mit einem Signifikanzniveau von  angenommen. Andernfalls wird
angenommen. Andernfalls wird  abgelehnt.
abgelehnt.
Arten von Hypothesentests
Angenommen, wir haben eine Grundgesamtheit  mit einem unbekannten Parameter
mit einem unbekannten Parameter  (der der Mittelwert, der Anteil oder die Standardabweichung sein kann). Die Tests werden dann als zweiseitig oder einseitig klassifiziert. Diese Tests sind in der folgenden Tabelle zusammengefasst:
(der der Mittelwert, der Anteil oder die Standardabweichung sein kann). Die Tests werden dann als zweiseitig oder einseitig klassifiziert. Diese Tests sind in der folgenden Tabelle zusammengefasst:
| Zweiseitig |  |  |
|---|---|---|
| Einseitig | 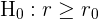 |  H_A: r < r_0[/latex] H_A: r < r_0[/latex] |
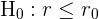 | 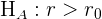 |
Zweiseitiger Test
Der zweiseitige Test ist gegeben, wenn die Nullhypothese die Form  hat. In diesem Fall hat die Alternativhypothese die Form
hat. In diesem Fall hat die Alternativhypothese die Form  .
.
Wenn 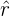 der Wert des Parameters in der Stichprobe ist, bedeutet dies, dass die Nullhypothese abgelehnt wird, wenn
der Wert des Parameters in der Stichprobe ist, bedeutet dies, dass die Nullhypothese abgelehnt wird, wenn 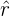 im Vergleich zu
im Vergleich zu  zu groß (oberer Bereich) oder zu klein (unterer Bereich) ist.
zu groß (oberer Bereich) oder zu klein (unterer Bereich) ist.
Für den Fall, dass wir den  Mittelwert der Grundgesamtheit untersuchen wollen, wird das Konfidenzintervall wie folgt konstruiert:
Mittelwert der Grundgesamtheit untersuchen wollen, wird das Konfidenzintervall wie folgt konstruiert:
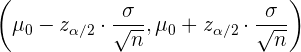
Für den Anteil  lautet das Konfidenzintervall
lautet das Konfidenzintervall
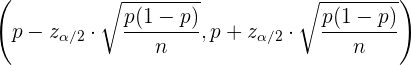
Einseitiger Test
Beim einseitigen Test gibt es zwei Fälle. Im ersten Fall ist die Nullhypothese vom Typ

und die Alternativhypothese lautet

In diesem Fall ist der Akzeptanzbereich bei der Überprüfung für den Mittelwert 

Der Akzeptanzbereich für den Anteil  ist
ist
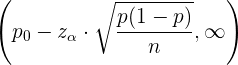
Im zweiten Fall ist die Nullhypothese vom Typ

und die Alternativhypothese lautet
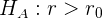
 kann
kann  oder
oder  sein.
sein.
Der Akzeptanzbereich bei der Überprüfung für den Mittelwert  ist somit
ist somit
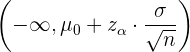
Der Akzeptanzbereich für den Anteil  ist
ist

Schließlich müssen wir beachten, dass in den einseitigen Tests die folgenden kritischen Werte am häufigsten vorkommen:
 |  | 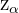 |
|---|---|---|
| 0,90 | 0,10 | 1,28 |
| 0,95 | 0,05 | 1,645 |
| 0,99 | 0,01 | 2,33 |
Fehlerarten
Bei der Durchführung von Hypothesentests besteht immer die Möglichkeit, Fehler zu machen. Fehler werden als Fehler vom Typ I und vom Typ II klassifiziert.
Ein Fehler vom Typ I tritt auf, wenn wir die Nullhypothese als wahr ablehnen.
Ein Fehler vom Typ II tritt hingegen auf, wenn wir die Nullhypothese annehmen und sie wahr ist.
Die Fehlerarten sind in der folgenden Tabelle zusammengefasst:
 | wahr | falsch |
|---|---|---|
| Akzeptieren | Richtige Entscheidung Wahrscheinlichkeit von  | Falsche Entscheidung Fehler Typ II |
| Ablehnen | Falsche Entscheidung Fehler Typ I Wahrscheinlichkeit von  | Richtige Entscheidung |
Die Wahrscheinlichkeit, einen Fehler vom Typ I zu begehen, ist das Signifikanzniveau  .
.
Andererseits wird die Wahrscheinlichkeit eines Fehlers vom Typ II üblicherweise mit  angegeben. In diesem Fall
angegeben. In diesem Fall 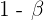 ist die Trennschärfe des Tests. Am besten lässt sich
ist die Trennschärfe des Tests. Am besten lässt sich  reduzieren, indem man den Stichprobenumfang
reduzieren, indem man den Stichprobenumfang  so weit wie möglich erweitert.
so weit wie möglich erweitert.
Mit KI zusammenfassen:












