Kapitel

Was ist eine Stichprobe?
Angenommen, wir haben eine Grundgesamtheit von  Objekten oder Individuen, die wir untersuchen wollen und die endlich oder unendlich sein kann. In vielen Situationen ist es unmöglich, jedes einzelne Individuum dieser Grundgesamtheit zu untersuchen.
Objekten oder Individuen, die wir untersuchen wollen und die endlich oder unendlich sein kann. In vielen Situationen ist es unmöglich, jedes einzelne Individuum dieser Grundgesamtheit zu untersuchen.
Um dieses Problem zu lösen, wird in der Regel eine Stichprobe aus der Grundgesamtheit gezogen. Eine Stichprobe ist eine Teilmenge  der Grundgesamtheit, das heißt
der Grundgesamtheit, das heißt 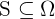 . Es gibt mehrere Methoden, um eine Stichprobe der Grundgesamtheit zu erhalten. Das Ziel jeder Methode ist jedoch, dass die Stichprobe repräsentativ für die Grundgesamtheit ist, d. h. dass die Eigenschaften der Stichprobe den Eigenschaften der Grundgesamtheit sehr ähnlich sind.
. Es gibt mehrere Methoden, um eine Stichprobe der Grundgesamtheit zu erhalten. Das Ziel jeder Methode ist jedoch, dass die Stichprobe repräsentativ für die Grundgesamtheit ist, d. h. dass die Eigenschaften der Stichprobe den Eigenschaften der Grundgesamtheit sehr ähnlich sind.
Sobald wir eine Stichprobe haben, wird die statistische Inferenz verwendet, um Schlussfolgerungen über die Grundgesamtheit zu ziehen. Statistische Inferenz ist also die Gesamtheit der Verfahren, mit denen aus einer gegebenen Stichprobe auf Eigenschaften der Grundgesamtheit „geschlossen“ werden kann.
Darüber hinaus gibt uns die statistische Inferenz auch Instrumente an die Hand, mit denen wir den Grad der Zuverlässigkeit oder des Konfidenzniveaus unserer Schlussfolgerungen bestimmen können.
Im Allgemeinen lassen sich die Stichprobenverfahren in zwei Kategorien einteilen: nichtstatistische Stichproben und Wahrscheinlichkeitsstichproben.
Nichtstatistische Stichprobe
Bei nichtstatistischen Stichprobenverfahren werden die Elemente der Stichprobe nicht anhand der Wahrscheinlichkeit (oder des Zufalls) ausgewählt.
Da sie keine Wahrscheinlichkeiten berücksichtigen, garantieren diese Methoden nicht, dass die Stichprobe repräsentativ ist. Daher sollten sie mit Vorsicht verwendet werden, um Verzerrungen der Schlussfolgerungen zu vermeiden. Außerdem sind diese Methoden anfällig für eine Unter- oder Überrepräsentation von Untergruppen in der Grundgesamtheit.
Dennoch haben diese Methoden einige Vorteile. Der wichtigste Vorteil ist, dass sie einfacher zu handhaben sind als Wahrscheinlichkeitsverfahren. Außerdem ist es in der Regel günstiger, mit diesen Verfahren eine Stichprobe zu erhalten, und in vielen Fällen ist es die einzige Möglichkeit, die wir haben, um die Stichprobe zu erhalten.
Aus diesen Gründen werden diese Stichprobenverfahren häufig hauptsächlich für „Pilotversuche“ verwendet, bevor anspruchsvollere statistische Verfahren zum Einsatz kommen.
Beispiele für nichtstatistische Stichprobenverfahren sind:
1 Zufallsstichprobe: Bei der Stichprobenziehung werden diejenigen Personen aus der Grundgesamtheit ausgewählt, die sich in unmittelbarer Nähe zu uns befinden. Sie wird auch als Gelegenheitsstichprobe bezeichnet.
Wir können zum Beispiel die Wahlpräferenzen unserer Stadt untersuchen, indem wir die Bewohner:innen unseres Viertels befragen. In diesem Fall sind die Grundgesamtheit die Einwohner:innen der Stadt und die Stichprobe sind die Einwohner:innen unseres Viertels.
2 Gezielte Stichprobe: In diesem Fall wird die Stichprobe auf der Grundlage eines Expertenurteils ausgewählt. Sie wird auch als beurteilende Stichprobe bezeichnet. Hierbei ist jedoch zu beachten, dass diese Methode mit einem randomisierten Verfahren kombiniert werden kann, wobei jedoch darauf geachtet werden muss, dass die Beurteilung keine Verzerrungen hervorruft.
Um zum Beispiel die Wahlpräferenzen in unserer Stadt zu untersuchen, schlägt ein Experte vor, dass  ,
,  und
und  die allgemeine Meinung der Stadt am besten repräsentieren.
die allgemeine Meinung der Stadt am besten repräsentieren.
Stichproben mit Wahrscheinlichkeitsfaktor
Bei der Wahrscheinlichkeitsstichprobe wird die Stichprobe nach dem Zufallsprinzip ausgewählt. Auf diese Weise hat jede Person in der Grundgesamtheit eine bekannte Wahrscheinlichkeit, ausgewählt zu werden. So hat jedes Individuum eine Chance, ausgewählt zu werden, und die Wahrscheinlichkeit, dass unsere Schlussfolgerungen verzerrt sind, wird verringert.
Jede Methode hat ihre eigenen Vor- und Nachteile. Die gängigsten sind im Folgenden aufgeführt.
Einfache Zufallsstichprobe
Bei einfachen Zufallsstichproben hat jede Person in der Grundgesamtheit die gleiche Wahrscheinlichkeit, für die Stichprobe ausgewählt zu werden.
Eine Möglichkeit, diese Stichprobe durchzuführen, besteht darin, die Elemente der Grundgesamtheit zu nummerieren und dann zufällig  Elemente auszuwählen. Es gibt jedoch zwei Möglichkeiten, diese Stichprobe durchzuführen:
Elemente auszuwählen. Es gibt jedoch zwei Möglichkeiten, diese Stichprobe durchzuführen:
1 Stichprobe mit Wiederholung: Sobald ein Element ausgewählt wurde, kann dasselbe Element bei der nächsten Entnahme erneut ausgewählt werden. Daher ist es möglich, dass eine Person mehr als einmal in der Stichprobe vertreten ist.
Obwohl es möglich ist, dass ein Element mehr als einmal in der Stichprobe wiederholt wird, ist dies in der Regel kein Nachteil für die Schlussfolgerungen, die wir ziehen. Außerdem hat es den Vorteil, dass die Berechnung der Inferenzen erleichtert wird.
2 Stichprobe ohne Wiederholung: In diesem Fall wird ein einmal ausgewähltes Element verworfen, wenn die restlichen Elemente ausgewählt werden. Jedes Element kann also maximal einmal ausgewählt werden.
Diese Methode hat den kleinen Vorteil, dass jedes Element höchstens einmal ausgewählt wird. Dies macht jedoch einige Berechnungen und Schätzungen etwas komplizierter.
Beispiel: In demselben Beispiel der Wahlpräferenzen in einer Stadt wählen wir zufällig  Nummern aus dem Wohnungsregister aus. Die Haushalte in diesen Wohnungen werden dann befragt.
Nummern aus dem Wohnungsregister aus. Die Haushalte in diesen Wohnungen werden dann befragt.
Wir stellen fest, dass die Kosten für diese Art der Stichprobenziehung etwas höher sind, da wir die Haushalte in einer großen Anzahl von Stadtvierteln besuchen müssen.
Systematische Zufallsstichprobe
Angenommen, wir haben eine Grundgesamtheit von  Elementen, die von 1 bis
Elementen, die von 1 bis  nummeriert sind, und wir möchten eine Stichprobe auswählen, die ein
nummeriert sind, und wir möchten eine Stichprobe auswählen, die ein  -tes Element der Grundgesamtheit ist.
-tes Element der Grundgesamtheit ist.
Dann wird eine zufällige Zahl  zwischen 1 und
zwischen 1 und  ausgewählt. Die restlichen Elemente werden in konstanten Intervallen (der Größe
ausgewählt. Die restlichen Elemente werden in konstanten Intervallen (der Größe  ) ausgewählt, bis die Stichprobe vollständig ist. Unsere Stichprobe besteht also aus den Elementen
) ausgewählt, bis die Stichprobe vollständig ist. Unsere Stichprobe besteht also aus den Elementen

Beispiel: Wenn wir eine Grundgesamtheit von 1000 Personen haben und 25 Elemente entnehmen möchten, dann ist das Verhältnis 

Dann wählen wir eine Zahl zwischen 1 und 40 (nehmen wir an, dass die Zufallszahl 24 ist). Die Stichprobe besteht also aus den Elementen
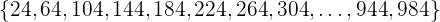
Diese Methode hat den Vorteil, dass die Stichprobe „gleichmäßiger“ über die gesamte Grundgesamtheit verteilt ist.
Geschichtete Zufallsstichprobe
Nehmen wir an, die Grundgesamtheit ist auf natürliche Weise in  Teilgesamtheiten unterteilt, und bezeichnen wir die Größe jeder Teilgesamtheit mit
Teilgesamtheiten unterteilt, und bezeichnen wir die Größe jeder Teilgesamtheit mit  ,
,  , …,
, …, 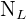 . Diese Teilgesamtheiten werden als Schichten bezeichnet.
. Diese Teilgesamtheiten werden als Schichten bezeichnet.
Bei geschichteten Stichproben ist es wichtig, dass sich die Schichten nicht überschneiden. Das heißt, dass kein Element zu mehr als einer Schicht gehört. Außerdem ist es wichtig, dass alle Elemente zu einer Schicht gehören.
Die geschichtete Stichprobe besteht aus einer einfachen Zufallsstichprobe innerhalb jeder Schicht. Das heißt, wir betrachten jede Schicht als Grundgesamtheit, um unsere Gesamtstichprobe zu bilden. Mit der geschichteten Stichprobe können wir genauere Schätzungen der Grundgesamtheit vornehmen, was allerdings etwas kompliziertere Berechnungen erfordert.
Das Hauptproblem bei geschichteten Stichproben besteht darin, den Stichprobenumfang innerhalb jeder Schicht zu bestimmen. Es gibt zwei Strategien:
1 Proportionale Schichtung: Wenn in diesem Fall der Gesamtstichprobenumfang  beträgt, dann ist der Stichprobenumfang jeder Schicht
beträgt, dann ist der Stichprobenumfang jeder Schicht
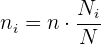
Diese Strategie hat den Vorteil, dass jede Schicht proportional vertreten ist.
2 Optimale Schichtung: In diesem Fall versuchen wir, die Varianz der Schätzungen innerhalb jeder Schicht zu minimieren. Daher haben die Schichten mit geringerer Varianz einen kleineren Stichprobenumfang.
Diese Strategie hat den Vorteil, dass wir viel genauere Schätzungen vornehmen können.
Beispiel:
In einer Fabrik mit 600 Arbeitnehmer:innen wollen wir eine Stichprobe von 20 nehmen. Wir wissen, dass es 200 Arbeitnehmer:innen im Bereich  , 150 in
, 150 in  , 150 in
, 150 in  und 100 in
und 100 in  gibt.
gibt.
Wenn beschlossen wird, eine geschichtete Stichprobe mit proportionaler Schichtung anzuwenden, welchen Umfang hat dann jede Schicht?
 sei dabei der Umfang der Grundgesamtheit und
sei dabei der Umfang der Grundgesamtheit und  der Umfang der allgemeinen Stichprobe. Analog dazu bezeichnen wir mit
der Umfang der allgemeinen Stichprobe. Analog dazu bezeichnen wir mit 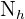 den Umfang der Schicht
den Umfang der Schicht  und mit
und mit  den Stichprobenumfang, den wir aus
den Stichprobenumfang, den wir aus  entnehmen. Da wir also eine proportionale Schichtung haben, gilt
entnehmen. Da wir also eine proportionale Schichtung haben, gilt
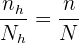
Das Problem besteht nur darin, die n_h-Werte für jede Schicht zu finden. Wir wissen bereits, dass die Grundgesamtheit 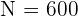 ist; der Umfang der jeweiligen Schichten beträgt
ist; der Umfang der jeweiligen Schichten beträgt 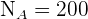 ,
, 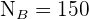 ,
, 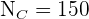 und
und 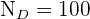 .
.
Außerdem wissen wir, dass 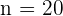 . Damit haben wir nun alle Daten, um den Stichprobenumfang für jede Schicht zu berechnen. Zunächst berechnen wir
. Damit haben wir nun alle Daten, um den Stichprobenumfang für jede Schicht zu berechnen. Zunächst berechnen wir  :
:
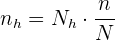
Für Bereich A nehmen wir also:

Für Bereich B:
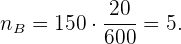
Für Bereich C:
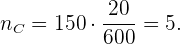
Und schließlich für Bereich D:

Schließlich überprüfen wir

Wenn wir jedoch das Gewicht der Arbeitnehmer:innen schätzen wollen und in Bereich  nur Personen arbeiten, von denen wir wissen, dass sie untergewichtig sind, dann könnten wir nur 2 Personen aus Bereich
nur Personen arbeiten, von denen wir wissen, dass sie untergewichtig sind, dann könnten wir nur 2 Personen aus Bereich  und den Rest aus den Bereichen
und den Rest aus den Bereichen  ,
,  und
und  auswählen. Der Stichprobenumfang sollte jedoch auf der Grundlage von Vorabinformationen über die Varianz gewählt werden.
auswählen. Der Stichprobenumfang sollte jedoch auf der Grundlage von Vorabinformationen über die Varianz gewählt werden.
Klumpenstichprobe
Bei Klumpenstichproben gehen wir davon aus, dass die Grundgesamtheit ebenfalls in  Schichten unterteilt ist. Bei der Klumpenstichprobe werden diese Schichten als Gruppen, Cluster oder Klumpen bezeichnet.
Schichten unterteilt ist. Bei der Klumpenstichprobe werden diese Schichten als Gruppen, Cluster oder Klumpen bezeichnet.
Wenn wir die Klumpen als 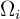 bezeichnen, dann besteht die Klumpenstichprobe darin, einige dieser Klumpen auszuwählen, und diese Klumpen bilden dann unsere Stichprobe. Mit anderen Worten: Wir betrachten jede Gruppe als ein Element und bilden eine Zufallsstichprobe aus den Gruppen.
bezeichnen, dann besteht die Klumpenstichprobe darin, einige dieser Klumpen auszuwählen, und diese Klumpen bilden dann unsere Stichprobe. Mit anderen Worten: Wir betrachten jede Gruppe als ein Element und bilden eine Zufallsstichprobe aus den Gruppen.
Diese Art der Stichprobe hat den Vorteil, dass sie kostengünstiger und einfacher sein kann als andere Arten von Stichproben, wobei die Zufälligkeit der Wahrscheinlichkeitsstichprobe erhalten bleibt.
Beispiel: Wenn wir die Wahlpräferenzen in einer Stadt untersuchen wollten, könnten wir anstelle einer einfachen Zufallsstichprobe einige Stadtteile zufällig auswählen. Dies hat den Vorteil, dass wir eine repräsentativere Stichprobe haben. Außerdem sind die Kosten im Vergleich zur einfachen Zufallsstichprobe geringer, da wir nicht alle Stadtteile besuchen müssen, sondern nur eine geringe Anzahl von Stadtteilen.
Verteilung der Stichprobenparameter
Bei einer Grundgesamtheit 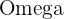 gibt es eine große Anzahl von Stichproben vom Umfang
gibt es eine große Anzahl von Stichproben vom Umfang  . Angenommen, wir wollen den Wert eines Parameters
. Angenommen, wir wollen den Wert eines Parameters  der Grundgesamtheit wissen, dann liefert jede dieser Grundgesamtheiten einen Schätzwert
der Grundgesamtheit wissen, dann liefert jede dieser Grundgesamtheiten einen Schätzwert  für diesen Parameter.
für diesen Parameter.
Wenn eine geeignete Stichprobe gezogen wird, liegen die meisten dieser Schätzungen nahe bei  . Allerdings ist zu beachten, dass
. Allerdings ist zu beachten, dass  von der gezogenen Stichprobe abhängt.
von der gezogenen Stichprobe abhängt.
Die Verteilung aller möglichen Werte von  wird als Stichprobenverteilung von
wird als Stichprobenverteilung von  bezeichnet. Wenn wir diese Verteilung kennen, können wir Rückschlüsse auf den Grundgesamtheitsparameter
bezeichnet. Wenn wir diese Verteilung kennen, können wir Rückschlüsse auf den Grundgesamtheitsparameter  ziehen.
ziehen.
Die am häufigsten untersuchten Parameter der Grundgesamtheit sind der Mittelwert  , die Varianz
, die Varianz 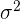 (oder Standardabweichung
(oder Standardabweichung  ) und das Verhältnis
) und das Verhältnis  .
.
Zentraler Grenzwertsatz
Der zentrale Grenzwertsatz ist einer der wichtigsten Sätze in der Statistik, da er es uns ermöglicht, die Normalverteilung zu nutzen, um Schätzungen für Grundgesamtheiten vorzunehmen, die nicht der Normalverteilung folgen.
Zentraler Grenzwertsatz. Wir nehmen die Stichprobe  vom Umfang
vom Umfang  aus der Grundgesamtheit
aus der Grundgesamtheit  und wenden die einfache Zufallsstichprobe an.
und wenden die einfache Zufallsstichprobe an.  sei der Mittelwert und
sei der Mittelwert und  die Standardabweichung von
die Standardabweichung von  . Wenn der Stichprobenumfang ausreichend groß ist, folgt der Stichprobenmittelwert
. Wenn der Stichprobenumfang ausreichend groß ist, folgt der Stichprobenmittelwert  annähernd einer Normalverteilung mit dem Mittelwert
annähernd einer Normalverteilung mit dem Mittelwert  und der Standardabweichung
und der Standardabweichung  . Je größer der Stichprobenumfang ist, desto eher nähert er sich der Normalverteilung an.
. Je größer der Stichprobenumfang ist, desto eher nähert er sich der Normalverteilung an.
Eine Faustregel für einen "ausreichend großen" Stichprobenumfang ist, dass  . Wenn also
. Wenn also  , können wir den zentralen Grenzwertsatz mit Sicherheit anwenden.
, können wir den zentralen Grenzwertsatz mit Sicherheit anwenden.
Die wichtigsten Schlussfolgerungen des zentralen Grenzwertsatzes sind:
1 Wenn wir bereits den Mittelwert  und die Standardabweichung
und die Standardabweichung  der Grundgesamtheit kennen, können wir die Wahrscheinlichkeit bestimmen, dass der Stichprobenmittelwert in einem bestimmten Bereich liegt.
der Grundgesamtheit kennen, können wir die Wahrscheinlichkeit bestimmen, dass der Stichprobenmittelwert in einem bestimmten Bereich liegt.
2 Wenn wir davon ausgehen, dass der Mittelwert  der Grundgesamtheit
der Grundgesamtheit 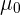 ist, dann können wir vorab wissen, in welchem Intervall der Stichprobenmittelwert liegen wird. Wenn der Stichprobenmittelwert nicht in diesem Intervall liegt, haben wir den Beweis, dass unsere Annahme falsch war.
ist, dann können wir vorab wissen, in welchem Intervall der Stichprobenmittelwert liegen wird. Wenn der Stichprobenmittelwert nicht in diesem Intervall liegt, haben wir den Beweis, dass unsere Annahme falsch war.
3 Ähnlich wie im vorherigen Fall können wir auch hier vorab wissen, in welchem Intervall die Summe der Elemente einer Stichprobe liegen wird. Die Summe der Elemente folgt der Verteilung, die wie folgt gegeben ist:
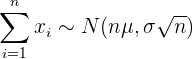
Beispiel:
Die von einer Maschine verpackten Salzbeutel haben ein Durchschnittsgewicht von  mit einer Standardabweichung von
mit einer Standardabweichung von 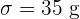 . Die Beutel werden in Kisten zu je 100 Stück verpackt.
. Die Beutel werden in Kisten zu je 100 Stück verpackt.
a Berechne die Wahrscheinlichkeit, dass der Durchschnitt der Gewichte der Beutel in einem Paket weniger als 495 g beträgt.
b Berechne die Wahrscheinlichkeit, dass eine Kiste mit 100 Beuteln mehr als 51 kg wiegt.
a Zur Beantwortung der ersten Frage muss man sich vergegenwärtigen, dass der Durchschnitt einer Stichprobe des Umfangs  näherungsweise einer Normalverteilung folgt (aufgrund des zentralen Grenzwertsatzes). Das heißt
näherungsweise einer Normalverteilung folgt (aufgrund des zentralen Grenzwertsatzes). Das heißt
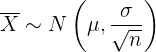
Die durchschnittliche Anzahl der Beutel in jeder Kiste folgt daher der folgenden Verteilung
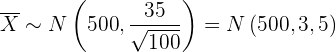
Wir berechnen also die Wahrscheinlichkeit wie folgt
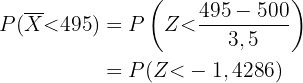 ,
,
wobei  eine Zufallsvariable mit Normalverteilung ist.
eine Zufallsvariable mit Normalverteilung ist.
Diese Wahrscheinlichkeit kann auf verschiedene Weise berechnet werden, zum Beispiel mit Excel oder einer Programmiersprache wie R.
Eine andere Möglichkeit, diese Wahrscheinlichkeit zu berechnen, ist die Verwendung einer Wahrscheinlichkeitstabelle der Normalverteilung, für die wir die Wahrscheinlichkeit wie folgt notieren müssen:
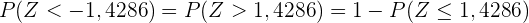
wir können nun 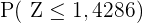 in der Tabelle suchen und erhalten
in der Tabelle suchen und erhalten 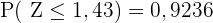 (ist der nächstliegende Wert, da er eine Genauigkeit von nur 2 Ziffern hat). Somit
(ist der nächstliegende Wert, da er eine Genauigkeit von nur 2 Ziffern hat). Somit
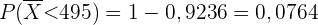
Bei Verwendung einer Programmiersprache ist das Ergebnis
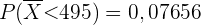 ,
,
was ziemlich ähnlich ist.
b Dieser Teilabschnitt ist ähnlich wie der vorherige. Der einzige Unterschied besteht darin, dass die Zufallsvariable jetzt die Summe der 100 Elemente der Stichprobe ist. In diesem Fall ergibt sich nach dem zentralen Grenzwertsatz
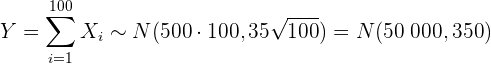 ,
,
wobei  das Gewicht einer jeden Kiste in Gramm ist. Somit liegt die gesuchte Wahrscheinlichkeit bei
das Gewicht einer jeden Kiste in Gramm ist. Somit liegt die gesuchte Wahrscheinlichkeit bei 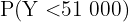 , da 51 kg 51.000 g entsprechen.
, da 51 kg 51.000 g entsprechen.
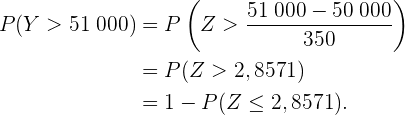
Wenn wir also eine Normalverteilungstabelle verwenden, ist das Ergebnis
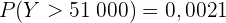
Wenn wir hingegen Excel oder eine Programmiersprache verwenden, lautet das Ergebnis
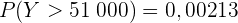
Wir denken daran, dass das mit einem Computer erzielte Ergebnis genauer ist.
Charakteristische Intervalle
Gegeben ist eine Zufallsvariable  . Das charakteristische Intervall
. Das charakteristische Intervall 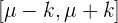 wird wie folgt berechnet:
wird wie folgt berechnet:
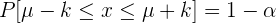
Diese Intervalle sind wichtig für die Erstellung von Schätzungen und Konfidenzintervallen. In diesem Zusammenhang werden üblicherweise die folgenden Begriffe verwendet:
1 Konfidenzintervall: 
2 Signifikanz oder Signifikanzniveau: 
3 Kritischer Wert: 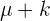 oder
oder  .
.
Man schreibt  zu
zu 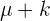 . Dies ist der Fall, wenn wir ein charakteristisches Intervall einer Standardnormalverteilung
. Dies ist der Fall, wenn wir ein charakteristisches Intervall einer Standardnormalverteilung  berechnen.
berechnen.
Beispiel: Finde das charakteristische Intervall einer Normalverteilung  , das einer Konfidenz von
, das einer Konfidenz von  entspricht.
entspricht.
Sieh dir folgende Abbildung an:
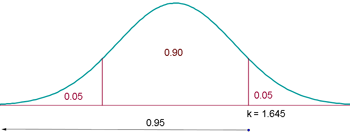
Wir stellen fest, dass 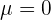 . Somit hat das Intervall die Form
. Somit hat das Intervall die Form 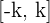 oder
oder 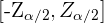 . An den Enden auf der linken und rechten Seiten beträgt die Wahrscheinlichkeit also 0,05 (d.h.
. An den Enden auf der linken und rechten Seiten beträgt die Wahrscheinlichkeit also 0,05 (d.h. 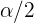 ). Es genügt somit, den Wert
). Es genügt somit, den Wert  zu bestimmen, so dass
zu bestimmen, so dass
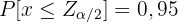
Dies kann auf verschiedene Weise geschehen: Man kann eine normale Tabelle verwenden, oder man kann den Befehl 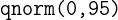 aus der Programmiersprache R verwenden.
aus der Programmiersprache R verwenden.
Unabhängig davon, welche Methode wir verwenden, würden wir 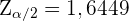 erhalten. Somit ist das charakteristische Intervall mit 90%-iger Sicherheit
erhalten. Somit ist das charakteristische Intervall mit 90%-iger Sicherheit
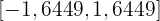
Tabelle der kritischen Werte
In der folgenden Tabelle sind die kritischen Werte für die Standardnormalverteilung  für gängige Konfidenzniveaus aufgeführt:
für gängige Konfidenzniveaus aufgeführt:
 | 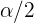 |  |
|---|---|---|
| 0,90 | 0,05 | 1,6448 |
| 0,95 | 0,025 | 1,9600 |
| 0,99 | 0,005 | 2,5758 |
Geht man von einer Normalverteilung 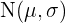 aus, so lassen sich die kritischen Intervalle aus den kritischen Werten der Verteilung
aus, so lassen sich die kritischen Intervalle aus den kritischen Werten der Verteilung  wie unten dargestellt berechnen:
wie unten dargestellt berechnen:
 | 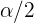 |  | Charakteristische Intervalle |
|---|---|---|---|
| 0,90 | 0,05 | 1,6449 | 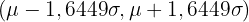 |
| 0,95 | 0,025 | 1,9600 | 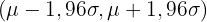 |
| 0,99 | 0,005 | 2,5758 | 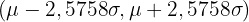 |
Mit KI zusammenfassen:












