Kapitel
Die Addition ist die mathematische Operation, bei der mehrere Zahlen zu einer einzigen zusammengefasst werden. Die Addition wird auch als Summenbildung bezeichnet. Die addierten Zahlen werden Summanden genannt, das Ergebnis Summe.
und 
sind die Summanden und das Ergebnis 
ist die Summe. Bei der Notation wird zwischen die Summanden das Zeichen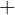 
geschrieben.
Beispiele:
Addition zweier einstelliger Zahlen
Die Summe zweier einstelliger Zahlen kann man im Kopf berechnen, sobald man sich die Additionstabelle eingeprägt hat:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
Addition einer einstelligen Zahl und einer beliebigen anderen Zahl
1 Die Einheiten der ersten Zahl werden zu denen der zweiten addiert.
2 Wenn die Summe größer als neun ist, wird eine Einheit zur Zahl hinzugefügt , die die Zehnerstelle angibt.
Addition mehrstelliger Zahlen
1 Die Zahlen werden untereinander geschrieben, sodass die Einer unter den Einern, die Zehner unter den Zehnern usw. stehen.
2 Die Einheiten der ersten Spalte werden addiert. Handelt es sich um eine einstellige Zahl, wird diese am Ende der Spalte geschrieben.
3 Wenn es mehr als eine Ziffer gibt, wird nur die Einerstelle am Ende der Spalte geschrieben, die Zehnerstelle wird in die nächste Spalte übertragen und dann ebenso fortgefahren.
Beziehung zwischen den Termen einer Summe
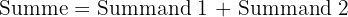
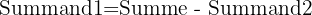
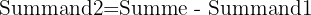
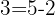
Regeln für die Addition natürlicher Zahlen
1 Interne Rechenoperation
Das Ergebnis der Addition zweier natürlicher Zahlen ist eine weitere natürliche Zahl.
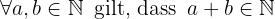
2 Assoziativ
Die Art und Weise, wie die Summanden angeordnet werden, hat keinen Einfluss auf das Ergebnis.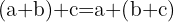
Beispiel:
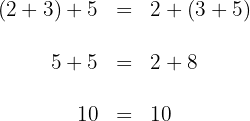
3 Kommutativ
Die Reihenfolge der Summanden ändert nichts an der Summe.
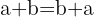
Beispiel:
4 Neutrales Element
Die 
ist das neutrale Element der Addition, da jede Zahl, die mit ihr addiert wird, dieselbe Zahl ergibt.
5 Die natürlichen Zahlen haben kein Gegenelement.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
