Kapitel
Die Teilbarkeit ist ein grundlegendes Konzept in der Mathematik, das es uns ermöglicht zu verstehen, wie sich Zahlen zueinander verhalten. Damit lässt sich feststellen, ob eine Zahl durch eine andere teilbar ist, ohne dass eine exakte Division erforderlich ist.
Durch Üben und Verstehen der Teilbarkeitsregeln wirst du die Fähigkeit entwickeln, Berechnungen zu vereinfachen, Zahlen zu faktorisieren und ein breites Spektrum an mathematischen Problemen zu lösen.
Primzahlen und zusammengesetzte Zahlen
Berechne alle Vielfachen von 17 zwischen 800 und 860.
Zuerst teilen wir 800 durch 17, was 47 ergibt, mit einem Rest von 1. Das bedeutet, dass 
kleiner ist als 800, aber 
ist größer als 800. Durch die Multiplikation erhalten wir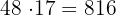 
Betrachtet man die auf 48 folgenden ganzen Zahlen, so ergibt sich
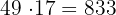
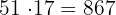
Wir stellen fest, dass 867 bereits größer ist als 860. Somit lautet das Ergebnis: 816, 833, 850
Gegeben sind die folgenden Zahlen: 179, 311, 848, 3566, 7287, welche sind Primzahlen und welche sind zusammengesetzte Zahlen?
Die Zahlen 848 und 3566 sind zusammengesetzte Zahlen, weil sie auf eine gerade Zahl enden und durch 2 teilbar sind.
Die Zahl 7287 ist ebenfalls eine zusammengesetzte Zahl, da sie durch 3 teilbar ist, da die Summe ihrer Ziffern durch 3 teilbar ist.
Die Zahl 179 ist eine Primzahl, da sie nicht durch 2, 3, 5, 7, 11 teilbar ist. Wir dividieren durch 13: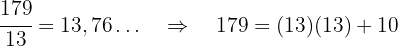 
Da die Division nicht genau aufgeht und der Quotient gleich dem Divisor ist, ist die Zahl eine Primzahl.
Die Zahl 311 ist eine Primzahl, weil sie nicht durch 2, 3, 5, 7, 11 teilbar ist. Wir dividieren durch 13: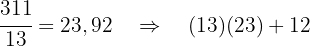
Wir fahren fort und sehen, dass die Division bis 311 nicht genau aufgeht. Es handelt sich also um eine Primzahl.
Berechne anhand einer Tabelle alle Primzahlen zwischen 400 und 450.
Wir müssen eine Tabelle wie die folgende konstruieren. Zuerst streichen wir alle geraden Zahlen, dann alle Vielfachen von 3, dann die Vielfachen von 5 und so weiter, bis wir 19 erreichen (die größte Primzahl, die sich faktorisieren lässt). Die Zahlen, die nicht durchgestrichen sind, sind Primzahlen
| 401 | 409 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 419 | |||||||||
| 421 | |||||||||
| 431 | 433 | 439 | |||||||
| 443 | 449 |
Primzahlen: 401, 409, 419, 421, 431, 433, 439, 443, 449
Faktorisieren
Zerlege die folgenden Faktoren in Faktoren:
216
360
432
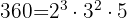
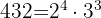
Faktorisiere die Zahl 342 und berechne ihre Anzahl der Teiler.
Zunächst zerlegen wir in Faktoren: 
Das heißt:
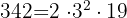
Wir addieren zu jedem der Exponenten der Faktoren von 342 eine Einheit und multiplizieren dann die erhaltenen Ergebnisse
Anzahl der Faktoren:
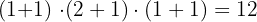
Zerlege die folgenden Zahlen in Faktoren:
2250
3500
2520
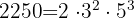
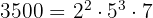
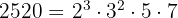
Größter gemeinsamer Teiler, kleinstes gemeinsames Vielfaches und euklidischer Algorithmus
Berechne den größten gemeinsamen Teiler (ggT) und das kleinste gemeinsame Vielfache (kgV) von:
- 428 und 376
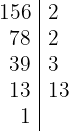
- 148 und 156
- 600 und 1 000
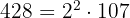und 
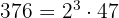. Um den ggT zu ermitteln, nehmen wir die gemeinsamen Faktoren des kleinsten Exponenten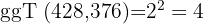 
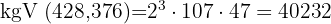
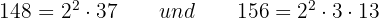
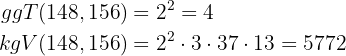
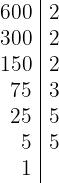
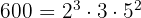und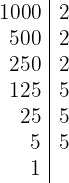 
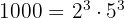. Mit den Faktoren erhalten wir den ggT: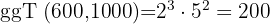 
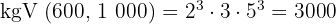
Berechne den ggT und das kgV von:
- 72, 108 und 60
- 1048, 786 und 3930
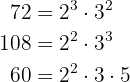
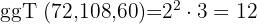
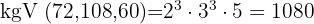
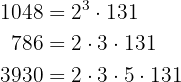
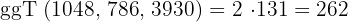
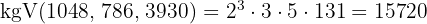
Berechne mithilfe des Euklidschen Algorithmus den ggT von:
- 72 und 16
- 656 und 848
- 1278 und 842
a 72 und 16: Zuerst teilen wir das größte (72) durch das kleinste (16). Wenn es keinen Rest gibt, ist 16 die größte gemeinsame Zahl. In diesem Fall erhalten wir
,
d.h. wir erhalten einen Rest von 8, also wiederholen wir den Vorgang und teilen den Divisor (16) durch den Rest (8). Wenn die Division genau aufgeht, dann ist 8 die größte gemeinsame Zahl:
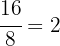
Somit ist 8 der ggT
b 656 und 848: Wenn wir den vorherigen Vorgang wiederholen, werden wir feststellen, dass die Division durch 848 und 656 nicht genau aufgeht. Wir teilen den Divisor (656) durch den erhaltenen Rest (192). Da auch diese Division nicht genau aufgeht, müssen wir den Divisor (80) durch den Rest (32) dividieren. Aber auch diese Division geht nicht genau auf. Nun dividieren wir den Divisor (32) durch den Rest (16)
Da die Division genau aufgeht, ist der ggT dieser letzten Division: 16.
c 1278 und 842: Zuerst teilen wir das größte (1278) durch das kleinste (842). Wenn es keinen Rest gibt, ist 842 die größte gemeinsame Zahl. In diesem Fall erhalten wir
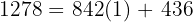
d.h. wir erhalten einen Rest von 436. Also wiederholen wir den Vorgang und teilen den Divisor (842) durch den Rest (436) und erhalten
Wir erhalten einen Rest von 406, also wiederholen wir den Vorgang und teilen den Divisor(436) durch den Rest(406), wobei wir einen Rest von 30 erhalten. Also ist es notwendig, den Vorgang zu wiederholen. Dieses Mal teilen wir 406 durch den Rest 30 und erneut geht die Division nicht genau auf
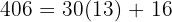
Der Rest ist 16 und wir wiederholen den Vorgang mit 30 und 16. Dieses Mal bleibt als Rest 14. Mit dem Divisor 16 und dem Rest 14 prüfen wir, ob die Division genau aufgeht, und wir prüfen, ob wir einen Rest von 2 erhalten. Das heißt, dass 14 nicht der ggT ist. Wir fahren mit 14 und 2 fort:
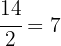
Die Division geht genau auf und wir erhalten den ggT (1278,842) = 2.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
