
Größter gemeinsamer Teiler
Der größte gemeinsame Teiler,  zweier oder mehr Zahlen ist die größte Zahl, durch die sich zwei ganze Zahlen ohne Rest teilen lassen.
zweier oder mehr Zahlen ist die größte Zahl, durch die sich zwei ganze Zahlen ohne Rest teilen lassen.
Berechnung des größten gemeinsamen Teilers
1Alle Zahlen werden in Primfaktoren zerlegt.
2Es werden die gemeinsamen Faktoren mit dem niedrigsten Exponenten genommen.
3Die gemeinsamen Faktoren mit dem niedrigsten Exponenten werden multipliziert.
Beispiel: Bestimme den  von:
von: 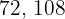 und
und 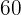 .
.
1Wir zerlegen die Zahlen in Primfaktoren

Die Zahlen werden also wie folgt geschrieben
2Die gemeinsamen Faktoren mit dem niedrigsten Exponenten sind 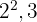
3Um den  zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
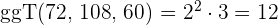
Wir beachten, dass wenn eine Zahl ein Teiler einer anderen Zahl ist, diese dann der  der beiden Zahlen ist
der beiden Zahlen ist
Beispiel: Die Zahl  ist ein Teiler von
ist ein Teiler von  , also
, also 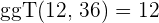
Kleinstes gemeinsames Vielfaches
Das kleinste gemeinsame Vielfache 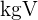 ist das kleinste gemeinsame Vielfache mehrerer Zahlen mit Ausnahme der Null.
ist das kleinste gemeinsame Vielfache mehrerer Zahlen mit Ausnahme der Null.
Berechnung des kleinsten gemeinsamen Vielfachen
1Wir zerlegen die Zahlen in Primfaktoren.
2Es werden die gemeinsamen Faktoren und die teilerfremden Faktoren mit dem höchsten Exponenten genommen.
3Es werden die gemeinsamen Faktoren und die teilerfremden Faktoren mit dem höchsten Exponenten multipliziert.
Beispiel: Bestimme das 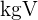 von:
von: 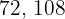 und
und 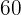 .
.
1Wir zerlegen die Zahlen in Primfaktoren

Die Zahlen werden also wie folgt geschrieben

2Die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten sind 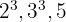
3Um das 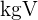 zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
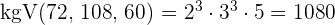
Somit ist 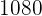 die kleinste Zahl die durch
die kleinste Zahl die durch 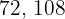 und
und 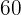 dividiert werden kann.
dividiert werden kann.
Beachte: Wenn eine Zahl ein Vielfaches einer anderen Zahl ist, ist diese das 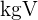 der beiden Zahlen.
der beiden Zahlen.
Beispiel: Die Zahl  ist ein Vielfaches von
ist ein Vielfaches von  , weshalb
, weshalb 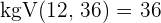
Beziehung zwischen dem größten gemeinsamen Teiler und dem kleinsten gemeinsamen Vielfachen
Da der größte gemeinsame Teiler und das kleinste gemeinsame Vielfache aus dem Produkt der gemeinsamen Faktoren mit dem niedrigsten Exponenten bzw. dem Produkt der gemeinsamen und der teilerfremden Faktoren mit dem höchsten Exponenten gebildet werden, gilt
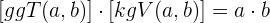
Übungen
Berechne den  und das
und das 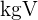 von
von  und
und 
1 Wir zerlegen die Zahlen in Primfaktoren

Die Zahlen werden also wie folgt geschrieben

2 Der Faktor mit dem niedrigsten Exponenten ist 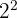
3 Um den  zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
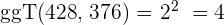
4 Die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten sind 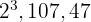
5 Um das 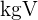 zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
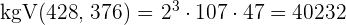
Berechne den  und das
und das 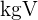 von
von  und
und 
1 Wir zerlegen die Zahlen in Primfaktoren

Die Zahlen werden also wie folgt geschrieben

2 Die gemeinsamen Faktoren mit dem niedrigsten Exponenten sind 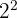
3 Um den  zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
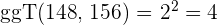
4 Die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten sind 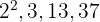
5 Um das 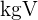 zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
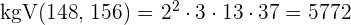
Berechne den  und das
und das 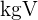 von
von  und
und 
1 Wir zerlegen die Zahlen in Primfaktoren
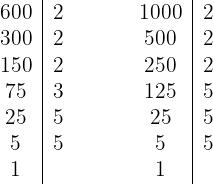
Die Zahlen werden also wie folgt geschrieben
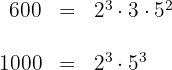
2 Die Faktoren mit dem niedrigsten Exponenten sind 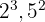
3 Um den  zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
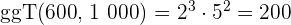
4 Die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten sind 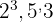
5 Um das 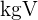 zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
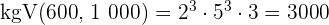
Berechne den  und das
und das 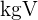 von
von  und
und 
1 Wir zerlegen die Zahlen in Primfaktoren
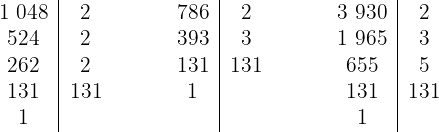
Die Zahlen werden also wie folgt geschrieben

2 Die Faktoren mit dem niedrigsten Exponenten sind 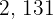
3 Um den  zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
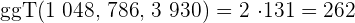
4 Die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten sind 
5 Um das 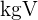 zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
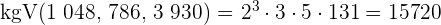
Berechne den  und das
und das 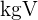 von
von 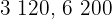 und
und 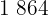
1 Wir zerlegen die Zahlen in Primfaktoren
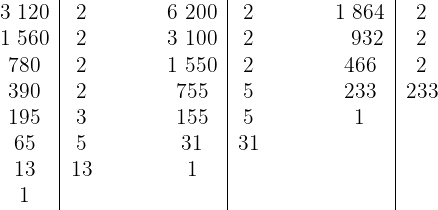
Die Zahlen werden also wie folgt geschrieben

2 Der Faktor mit dem niedrigsten Exponenten ist 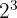
3 Um den  zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen Faktoren mit dem niedrigsten Exponenten
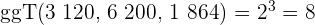
4 Die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten sind 
5 Um das 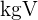 zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
zu berechnen, multiplizieren wir die gemeinsamen und teilerfremden Faktoren mit dem höchsten Exponenten
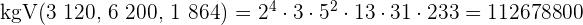
Ein Scheinwerfer schaltet sich alle  Sekunden ein, an anderer alle
Sekunden ein, an anderer alle  Sekunden und ein dritter jede Minute. Um
Sekunden und ein dritter jede Minute. Um 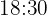 Uhr sind alle Scheinwerfer gleichzeitig eingeschaltet. Auf welche Uhrzeit trifft das noch zu?
Uhr sind alle Scheinwerfer gleichzeitig eingeschaltet. Auf welche Uhrzeit trifft das noch zu?
1 Wir zerlegen die Zahlen in Primfaktoren
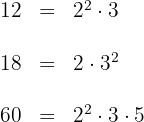
2 Wir berechnen das 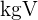 der drei Zahlen
der drei Zahlen
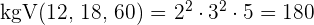
3 Die Scheinwerfer treffen alle 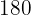 Sekunden zusammen, was
Sekunden zusammen, was  Minuten entspricht; Die Uhrzeit ist also
Minuten entspricht; Die Uhrzeit ist also 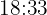 Uhr
Uhr
Ein Reisender fährt alle  Tage nach Barcelona, ein anderer alle
Tage nach Barcelona, ein anderer alle  Tage. Heute waren sie beide in Barcelona. In wie vielen Tagen werden wieder beide zur gleichen Zeit in Barcelona sein?
Tage. Heute waren sie beide in Barcelona. In wie vielen Tagen werden wieder beide zur gleichen Zeit in Barcelona sein?
1 Wir zerlegen die Zahlen in Primfaktoren
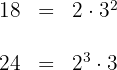
2 Wir berechnen das 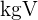 der zwei Zahlen
der zwei Zahlen
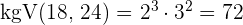
3 Die beiden Reisenden werden in  Tagen wieder gleichzeitig in Barcelona sein.
Tagen wieder gleichzeitig in Barcelona sein.
Wie lautet die kleinste Zahl, die bei separater Division durch  und
und 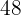 jeweils
jeweils  als Rest ergibt?
als Rest ergibt?
1 Wir zerlegen die Zahlen in Primfaktoren

2 Wir berechnen das 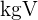 der vier Zahlen
der vier Zahlen
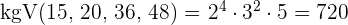
3 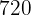 ist die kleinste Zahl, die durch die vier Zahlen teilbar ist. Wenn wir also durch die vier Zahlen dividieren wollen, um den Rest
ist die kleinste Zahl, die durch die vier Zahlen teilbar ist. Wenn wir also durch die vier Zahlen dividieren wollen, um den Rest  zu erhalten, muss die Zahl
zu erhalten, muss die Zahl 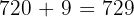 sein.
sein.
In einem Weinkeller gibt es  Weinfässer, die ein Fassungsvermögen von
Weinfässer, die ein Fassungsvermögen von 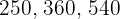 Litern haben. Der Inhalt soll in eine bestimmte Anzahl von gleich großen Korbflaschen abgefüllt werden. Berechne das maximale Fassungsvermögen dieser Behältnisse, so dass der in jedem der Fässer enthaltene Wein in sie gefüllt werden kann, und die Anzahl der erforderlichen Behältnisse.
Litern haben. Der Inhalt soll in eine bestimmte Anzahl von gleich großen Korbflaschen abgefüllt werden. Berechne das maximale Fassungsvermögen dieser Behältnisse, so dass der in jedem der Fässer enthaltene Wein in sie gefüllt werden kann, und die Anzahl der erforderlichen Behältnisse.
1 Wir zerlegen die Zahlen in Primfaktoren
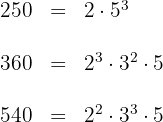
2 Wir berechnen den  der drei Zahlen
der drei Zahlen
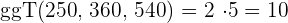
3 Das Fassungsvermögen jeder Flasche beträgt  Liter und die Anzahl der Flaschen ist
Liter und die Anzahl der Flaschen ist  .
.
Der Boden eines Zimmers soll geflieset werden. Die Länge des Zimmers beträgt 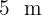 und die Breite
und die Breite 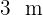 . Berechne die Seite in Dezimetern und die Anzahl der Fliesen so, dass die Anzahl der zu verlegenden Fliesen möglichst gering ist und keine Fliesen geschnitten werden müssen.
. Berechne die Seite in Dezimetern und die Anzahl der Fliesen so, dass die Anzahl der zu verlegenden Fliesen möglichst gering ist und keine Fliesen geschnitten werden müssen.
1 Der Boden des zu verfliesenden Raumes hat folgende Maße:  Länge und
Länge und 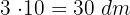 Breite.
Breite.
2 Wir berechnen den  der drei Zahlen
der drei Zahlen
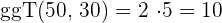
3 Die Seite jeder Fliese misst 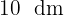 und es werden
und es werden  Fliesen in der Länge und
Fliesen in der Länge und in der Breite benötigt. Ingesamt also
in der Breite benötigt. Ingesamt also 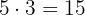 Fliesen.
Fliesen.
Ein Händler möchte 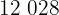 Äpfel und
Äpfel und 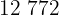 Orangen in Kisten verpacken, so dass jede Kiste die gleiche Anzahl von Äpfeln oder Orangen und so viele wie möglich enthält. Bestimme die Anzahl der Orangen in jeder Kiste und die Anzahl der benötigten Kisten.
Orangen in Kisten verpacken, so dass jede Kiste die gleiche Anzahl von Äpfeln oder Orangen und so viele wie möglich enthält. Bestimme die Anzahl der Orangen in jeder Kiste und die Anzahl der benötigten Kisten.
1 Wir berechnen den 
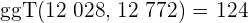
2 Wie berechnen die Anzahl der benötigten Kisten

Die Anzahl der benötigten Kisten lautet 
Welche Maße hat die größte quadratische Fliese, die genau gleich oft in einen Raum mit einer Länge von  und einer Breite von
und einer Breite von 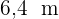 passt? Und wie viele Fliesen werden benötigt?
passt? Und wie viele Fliesen werden benötigt?
1 Der Boden des zu verfliesenden Raumes hat folgende Maße:  Länge und
Länge und 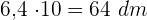 Breite
Breite
2 Wir berechnen den  der zwei Zahlen
der zwei Zahlen
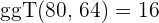
3 Die Seite jeder Fliese misst 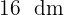 und es werden
und es werden 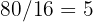 Fliesen in der Länge und
Fliesen in der Länge und 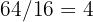 in der Breite benötigt. Insgesamt werden somit
in der Breite benötigt. Insgesamt werden somit  Fliesen benötigt.
Fliesen benötigt.
Mit KI zusammenfassen:













