Vervollständige:
| 1 |  |  |  |  | |
 |  |  |
Da beide Brüche denselben Nenner haben, bleibt der Nenner gleich und die Zähler werden addiert

| 2 |  |  |  |  | |
 |  |  |
Da beide Brüche denselben Nenner haben, bleibt der Nenner gleich und wir subtrahieren die Zähler

| 3 |  |  |  |  | |
 |  |  |
Die Brüche haben unterschiedliche Nenner und können nicht einfach addiert oder subtrahiert werden. In diesen Fällen berechnen wir das kleinste gemeinsame Vielfache der Nenner  und
und 
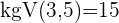
Hier berechnen wir mit dem kgV im Nenner


Wir addieren die Brüche mit demselben Nenner

| 4 |  |  |  |  | |
 |  |  |
Die Brüche haben unterschiedliche Nenner und können nicht einfach addiert oder subtrahiert werden. In diesen Fällen berechnen wir das kleinste gemeinsame Vielfache der Nenner von  und
und 
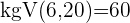
Hier berechnen wir mit dem kgV im Nenner


Wir addieren die Brüche mit demselben Nenner

| 5 |  |  |  |  | |
 |  |
Die Brüche haben unterschiedliche Nenner und somit können die Zähler nicht einfach addiert oder subtrahiert werden. In diesen Fällen berechnen wir das kleinste gemeinsame Vielfache der Nenner von  und
und 
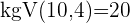
Hier berechnen wir mit dem kgV im Nenner


Wir addieren die Brüche mit demselben Nenner

| 6 |  |  |  |  | |
 |  |
Die Brüche haben unterschiedliche Nenner und somit können die Zähler nicht einfach addiert oder subtrahiert werden. In diesen Fällen berechnen wir das kleinste gemeinsame Vielfache der Nenner von  und
und 
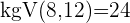
Hier berechnen wir mit dem kgV im Nenner


Wir subtrahieren die Brüche mit demselben Nenner

| 7 |  |  |  |  |  |  | |
 |  |  |  |
Da alle drei Brüche denselben Nenner haben, bleibt der Nenner gleich und die Zähler werden addiert

| 8 |  |  |  |  |  |  | |
 |  |  |  |
Da alle drei Brüche denselben Nenner haben, bleibt der Nenner gleich und die Zähler werden subtrahiert

| 9 |  |  |  |  |  |  | |
 |  |  |
Da alle drei Brüche denselben Nenner haben, bleibt der Nenner erhalten und die Berechnungen werden mit den Zählern durchgeführt

| 10 |  |  |  |  |  |  | |
 |  |  |
Da alle drei Brüche denselben Nenner haben, bleibt der Nenner gleich und die Berechnungen werden mit den Zählern durchgeführt

Wir stellen fest, dass im vorherigen Ergebnis der Zähler und der Nenner Vielfache von 3 sind, sodass wir vereinfachen

| 11 |  |  |  |  |  |  | |
 |  |  |
Die Brüche haben unterschiedliche Nenner und somit können die Zähler nicht einfach addiert oder subtrahiert werden. In diesen Fällen berechnen wir das kleinste gemeinsame Vielfache der Nenner von  und
und 
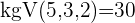
Hier berechnen wir mit dem kgV im Nenner



Wir addieren die Brüche mit demselben Nenner

| 12 |  |  |  |  |  |  | |
 |  |  |
Die Brüche haben unterschiedliche Nenner und somit können die Zähler nicht einfach addiert oder subtrahiert werden. In diesen Fällen berechnen wir das kleinste gemeinsame Vielfache der Nenner von  und
und 
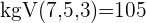
Hier berechnen wir mit dem kgV im Nenner



Wir subtrahieren die Brüche mit demselben Nenner
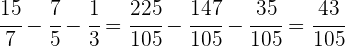
| 13 |  |  |  |  |  |  | |
 |  |  |
Die Brüche haben unterschiedliche Nenner und somit können die Zähler nicht einfach addiert oder subtrahiert werden. In diesen Fällen berechnen wir das kleinste gemeinsame Vielfache der Nenner von  und
und 
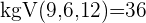



Wir addieren und subtrahieren die Brüche mit demselben Nenner

| 14 |  |  |  |  |  |  | |
 |  |  |
Die Brüche haben unterschiedliche Nenner und somit können die Zähler nicht einfach addiert oder subtrahiert werden. In diesen Fällen berechnen wir das kleinste gemeinsame Vielfache der Nenner von  und
und 
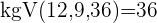
Hier berechnen wir mit dem kgV im Nenner



Wir addieren und subtrahieren die Brüche mit demselben Nenner

| 15 |  |  |  |  |  |  | |
 |  |  |
Die Brüche haben unterschiedliche Nenner und somit können die Zähler nicht einfach addiert oder subtrahiert werden. In diesen Fällen berechnen wir das kleinste gemeinsame Vielfache der Nenner von  und
und 
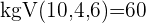
Hier berechnen wir mit dem kgV im Nenner



Wir addieren die Brüche mit demselben Nenner

Mit KI zusammenfassen:


