Eine umgekehrt proportionale Verteilung bedeutet, dass wir bei gegebenen Größen derselben Art und einer Gesamtgröße eine Verteilung vornehmen müssen, die direkt proportional zu den Kehrwerten der Größen ist.

Beispiel für eine umgekehrt proportionale Verteilung
Während der Testamentseröffnung verlas der Anwalt von Herrn Müller den folgenden Absatz über das Erbe, das er seinen Kindern hinterlassen wollte: “… An meine Kinder Henri, Patrick und Luis möchte ich den Betrag von 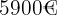 vererben. Die Aufteilung muss so erfolgen, dass sie einen Betrag erhalten, der umgekehrt proportional zu ihrem Alter zum Zeitpunkt meines Todes ist...” Wenn Henri, Patrick und Luis jeweils
vererben. Die Aufteilung muss so erfolgen, dass sie einen Betrag erhalten, der umgekehrt proportional zu ihrem Alter zum Zeitpunkt meines Todes ist...” Wenn Henri, Patrick und Luis jeweils 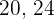 und
und  Jahre alt sind, wie viel erhält dann jeder von Ihnen?
Jahre alt sind, wie viel erhält dann jeder von Ihnen?
Schritte zur Ermittlung der Lösung
Da die Verteilung umgekehrt proportional erfolgt, erhält das jüngere Kind einen größeren Anteil des Erbes, während das ältere Kind einen geringeren Anteil erhält. Dies lässt sich lösen, indem man die Kehrwerte der Altersangaben ermittelt und eine direkt proportionale Verteilung zwischen diesen und dem Gesamtbetrag vornimmt.
1 Wir ermitteln die Kehrwerte des jeweiligen Alters
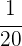

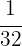
2 Wir bringen die Brüche auf einen gemeinsamen Nenner (denke daran, dass du das kgV anwenden kannst)
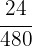
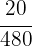
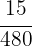
3 Wir nehmen eine direkt proportionale Verteilung der Zähler vor.:  und
und  .
.
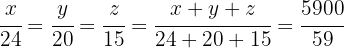
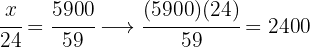
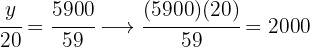
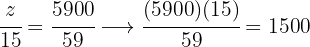
Henri erhält also 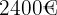 , Patrick
, Patrick 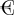 und Luis
und Luis 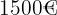 .
.
Mit KI zusammenfassen:












