Kapitel
Fläche eines Dreiecks
Gegeben seien die beiden Vektoren 
und 
, die ein Dreieck bilden. Anhand der grafischen Darstellung ist zu erkennen, welche beiden Seiten des Dreiecks durch die Vektoren festgelegt sind. Folgende Formel lässt sich zur Berechnung der Dreiecksfläche ableiten:
Beispiel:
Bestimme die Fläche des Dreiecks mit den Scheitelpunkten 
, 
und 
Das Dreieck setzt sich aus folgenden Vektoren zusammen
Berechne das Vektorprodukt
Man erhält als Ergebnisvektor
Um die Fläche zu erhalten, verwendet man folgende Formel
Fläche eines Parallelogramms
Geometrisch gesehen ist das Vektorprodukt zweier Vektoren die Flächenmaßzahl des Parallelogramms, das durch die beiden Vektoren aufgespannt wird.
Beispiel:
Ermittle das Flächenmaß des Parallelogramms, dessen Seiten durch die Vektoren 
y 
festgelegt sind.
Berechne zuerst das Vektorprodukt
Man erhält (wie bei der Formel für die Fläche) den Ergebnisvektor
Volumen eines Tetraeders
Das Volumen eines Tetraeders lässt sich mithilfe des Spatprodukts berechnen.
Beispiel:
Ermittle das Volumen des Tetraeders mit den Scheitelpunkten 
, 
, 
und 
.
Das Tetraeder wird von folgenden Vektoren aufgespannt
Verwende die Formel für Volumina
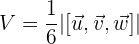
Berechne das Spatprodukt
Das Volumen ist
Volumen eines Parallelepipeds
Geometrisch gesehen repräsentiert der Wert des Spatprodukts das Volumen des Parallelepipeds dessen Kanten aus drei Vektoren aufgespannt werden, die alle demselben Scheitelpunkt entspringen
Beispiel:
Ermittle das Volumen des Parallelepipeds, das durch die folgenen drei Vektoren aufgespannt wird:
Berechne das Spatprodukt
Abstand zwischen parallelen Ebenen
Um den Abstand zwischen zwei parallelen Ebenen zu bestimmen, gibt es zwei unterschiedliche Rechenwege, je nach dem, welche Daten zur Berechnung vorliegen:
1 Die Gleichung einer der Ebenen und ein Punkt auf der anderen Ebene sind bekannt:
Um den Abstand zwischen den beiden parallelen Ebenen zu finden, berechnet man den Abstand von einem beliebigen Punkt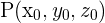 
von einer der Ebenen zur anderen Ebene 
mithilfe der folgenden Formel:
2 Die Gleichung der beiden Ebenen sind bekannt:
Alternativ kann dieser Rechenweg herangezogen werden
Wenn die Ebenen parallel zueinander sind, besitzen ihre Gleichungen diese Form:
und ihr Abstand ist wie folgt
Gleichermaßen gilt für den gegenteiligen Fall, dass die Gleichungen nicht der genannten Form entsprechen
Damit beide Ebenen parallel zueinander sind, muss Folgendes erfüllt sein
Eine der beiden Gleichungen muss so multipliziert werden, dass beide Ebenen den selben Normalvektor in ihren Gleichungen aufweisen. Das heißt, beide müssen folgender Form entsprechen:
Nun kann die Abstandsformel angewandt werden
Beispiel:
Berechne den Abstand zwischen den beiden Ebenen:
.
Prüfe zuerst ihre Parallelität. Nimm hierfür zuerst den Quotienten des Koeffizienten von 
und 
durch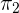 
. Dieser muss gleich dem Quotienten des Koeffizienten von 
und von 
sein. Jedoch muss er ungleich dem Qutienten der konstanten Glieder sein, da die Ebenen dann nicht parallel, sondern identisch wären.
Die beiden Ebenen sind parallel.
Schreibe die Gleichung der zweiten Ebene um, sodass beide Ebenen denselben Normalvektor aufweisen
Verwende die Abstandsformel für zwei Ebenen
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
