Kapitel

Winkel zwischen zwei Geraden
Der Winkel, der zwischen zwei Geraden entsteht, entspricht dem spitzen Winkel, der sich aus den Richtungsvektoren der Geraden ergibt.
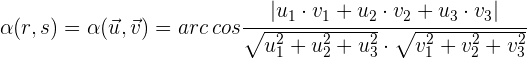
Zwei Geraden sind zueinander senkrecht, wenn die Richtungsvektoren orthogonal sind, das heisst, wenn 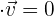
Aufgaben zum Winkel zwischen zwei Geraden
Bestimme den Winkel, den die Geraden bilden:

1 Wir erhalten den Richtungsvektor  der Geraden
der Geraden 
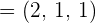
2 Wir erhalten den Richtungsvektor  der Geraden
der Geraden 
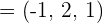
3 Wir setzen in die Formel zur Bestimmung des Winkels zwischen zwei Geraden ein und lösen
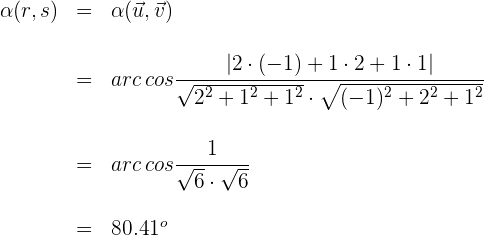
Der Winkel, den die zwei Geraden bilden ist also 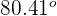
Bestimme den Winkel, den die Geraden bilden:

1 Wir erhalten den Richtungsvektor  der Geraden
der Geraden  . Da
. Da  den Bereich darstellt, indem sich zwei zueinander senkrechte Ebenen schneiden, wenden wir die Formel zur Bestimmung des Richtungsvektors an. Hierbei kommen die Koeffizienten der Ebenen zur Anwendung
den Bereich darstellt, indem sich zwei zueinander senkrechte Ebenen schneiden, wenden wir die Formel zur Bestimmung des Richtungsvektors an. Hierbei kommen die Koeffizienten der Ebenen zur Anwendung
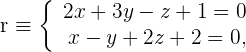

Der Richtungsvektor ist
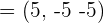
2 Wir erhalten den Richtungsvektor  der Geraden
der Geraden 

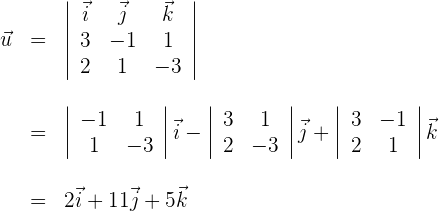
Der Richtungsvektor ist

3Wir setzen in die Formel zur Bestimmung des Winkels zwischen zwei Geraden ein und lösen
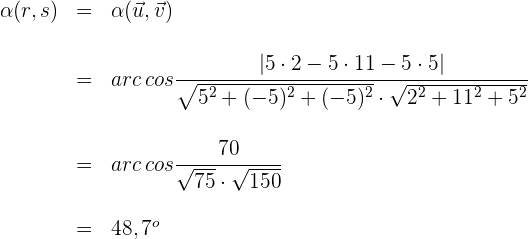
Der Winkel, der durch die zwei Geraden gebildet wird, ist also 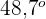
Bestimme den Winkel, den die Geraden bilden:
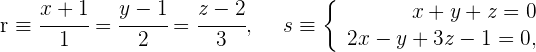
1 Wir erhalten den Richtungsvektor  der Geraden
der Geraden  .
.
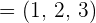
2 Wir erhalten den Richtungsvektor  der Geraden
der Geraden  . Da
. Da  die Überschneidung zweier zueinander senkrechten Ebenen darstellt, wenden wir die Formel zur Bestimmung des Richtungsvektor an. Hierbei kommen die Koeffizienten der zueinander senkrechten Ebenen zur Anwendung.
die Überschneidung zweier zueinander senkrechten Ebenen darstellt, wenden wir die Formel zur Bestimmung des Richtungsvektor an. Hierbei kommen die Koeffizienten der zueinander senkrechten Ebenen zur Anwendung.
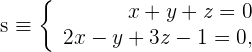
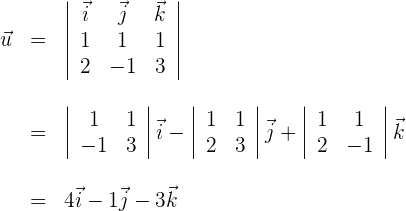
Der Richtungsvektor ist

3 Wir setzen in die Formel zur Bestimmung des Winkels zwischen zwei Geraden ein und lösen
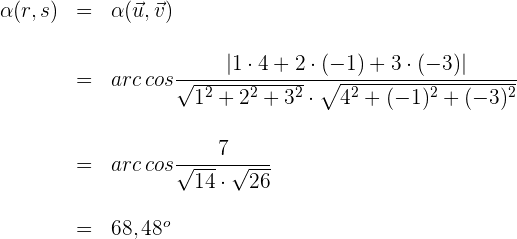
Der von den zwei Geraden gebildete Winkel ist also 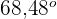
Winkel zwischen zwei Ebenen
Der von zwei Ebenen gebildete Winkel ist gleich dem spitzen Winkel, der durch die Normalenvektoren 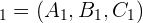 und
und 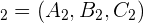 der besagten Ebenen entstehen.
der besagten Ebenen entstehen.

Zwei Ebenen sind senkrecht zueinander 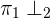 , wenn ihre Normalenvektoren orthogonal sind. Das heisst, wenn
, wenn ihre Normalenvektoren orthogonal sind. Das heisst, wenn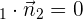
Aufgaben zum Winkel zwischen zwei Ebenen
Winkel zwischen Gerade und Ebene
Der Winkel, den eine Gerade  und eine Ebene
und eine Ebene  bilden, ist der Winkel, der durch
bilden, ist der Winkel, der durch  mit seiner orthogonalen Abbildung auf
mit seiner orthogonalen Abbildung auf  entsteht.
entsteht.

Der Winkel zwischen einer Geraden und einer Ebene ist der Komplementärwinkel des spitzen Winkels zwischen dem Richtungsvektor 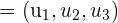 der Geraden und dem Normalenvektor
der Geraden und dem Normalenvektor 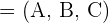 der Ebene.
der Ebene.

Wenn die Gerade  und die Ebene
und die Ebene  senkrecht sind, haben der Richtungsvektor der Geraden und der Normalenvektor der Ebene dieselbe Richtung. Ihre Komponenten sind also proportional
senkrecht sind, haben der Richtungsvektor der Geraden und der Normalenvektor der Ebene dieselbe Richtung. Ihre Komponenten sind also proportional
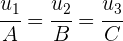
Aufgabe zum Winkel zwischen einer Geraden und einer Ebene
Bestimme den Winkel, den Gerade und Ebene bilden:
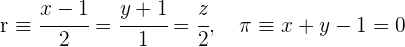
1 Wir erhalten den Richtungsvektor  der Geraden
der Geraden 
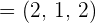
2 Wir erhalten den Normalenvektor 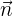 der Ebene
der Ebene  . Dieser ist durch die Koeffizienten der Gleichung der Ebene gegeben
. Dieser ist durch die Koeffizienten der Gleichung der Ebene gegeben
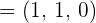
3 Wir setzen in die Formel zur Bestimmung des Winkels zwischen einer Geraden und einer Ebene ein und lösen
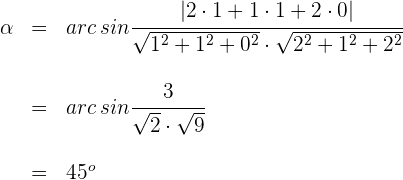
Der Winkel zwischen Gerade und Ebene ist also 
Bestimme den Winkel, den Gerade und Ebene bilden:
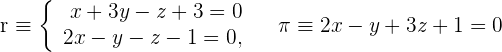
1 Wir erhalten den Richtungsvektor der Geraden
der Geraden  . Da
. Da  den Bereich darstellt, an dem sich zwei zueinander senkrechte Ebenen schneiden, wenden wir die Formel zur Bestimmung des Richtungsvektors an. Hierbei kommen die Koeffizienten der Ebenen zur Anwendung.
den Bereich darstellt, an dem sich zwei zueinander senkrechte Ebenen schneiden, wenden wir die Formel zur Bestimmung des Richtungsvektors an. Hierbei kommen die Koeffizienten der Ebenen zur Anwendung.
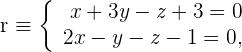

Der Richtungsvektor ist

2 Wir erhalten den Normalenvektor 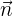 der Ebene
der Ebene  . Dieser ist durch die Koeffizienten der Gleichung der Ebene gegeben
. Dieser ist durch die Koeffizienten der Gleichung der Ebene gegeben

3 Wir setzen in die Formel zur Bestimmung des Winkels zwischen einer Geraden und einer Ebene ein und lösen
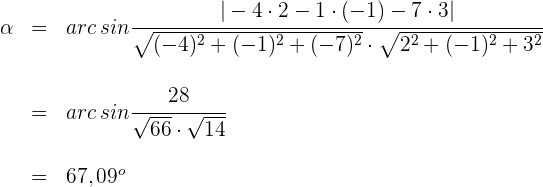
Der Winkel zwischen Gerade und Ebene ist also 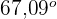
Bestimme den Winkel, den die Gerade und die Ebene bilden:
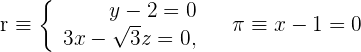
1 Wir erhalten den Richtungsvektor  der Geraden
der Geraden  . Da
. Da  den Bereich darstellt, in dem sich zwei zueinander senkrechte Ebenen schneiden, wenden wir die Formel zur Bestimmung des Richtungsvektors an. Hierbei kommen die Koeffizienten der Ebenen zur Anwendung.
den Bereich darstellt, in dem sich zwei zueinander senkrechte Ebenen schneiden, wenden wir die Formel zur Bestimmung des Richtungsvektors an. Hierbei kommen die Koeffizienten der Ebenen zur Anwendung.
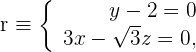
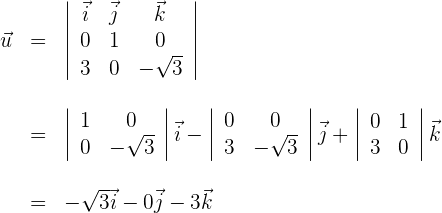
Der Richtungsvektor ist

2 Wir erhalten den Normalenvektor 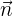 einer Ebene
einer Ebene  . Dieser ist durch die Koeffizienten der Gleichung der Ebene gegeben.
. Dieser ist durch die Koeffizienten der Gleichung der Ebene gegeben.
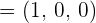
3 Wir setzen in die Formel zur Bestimmung des Winkels zwischen einer Geraden und einer Ebene ein und lösen
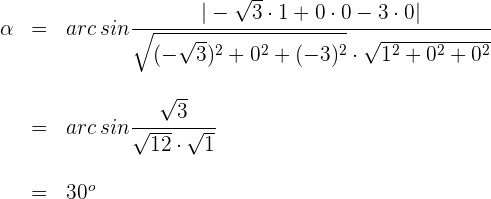
Der gesuchte Winkel zwischen Gerade und Ebene ist also 













