Ermittle den unbekannten Term und gib seine Bezeichnung in den folgenden Operationen an:
a 
b 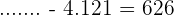
c 
d 
a 
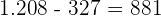

Ein Summand ist gleich der Summe minus dem anderen Summanden
b 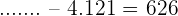


Der Minuend ist gleich der Differenz + Subtrahend
c 
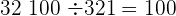

Ein Faktor ist gleich dem Produkt geteilt durch den anderen Faktor
d 


Der Divisor ist gleich dem Dividenden geteilt durch den Quotienten
Finde den unbekannten Term in den folgenden Operationen:
a 
b 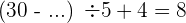
c 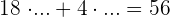
d 
Finde den unbekannten Term in den folgenden Operationen:
Lösung:
a 
Ein Faktor ist gleich dem Produkt geteilt durch den anderen Faktor
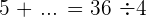

Ein Summand ist gleich der Summe minus dem anderen Summanden

b 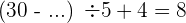
Ein Summand ist gleich der Summe minus dem anderen Summanden
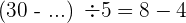
Wir subtrahieren
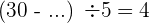
Dividend ist gleich Divisor mal Quotient
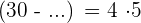
Wir multiplizieren

Subtrahend ist gleich Minuend minus Differenz
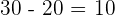
c 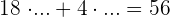
Wir klammern den gemeinsamen Faktor  aus dem ersten Term aus
aus dem ersten Term aus
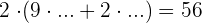
Ein Faktor ist gleich dem Produkt geteilt durch den anderen Faktor

Wir dividieren


d 
Subtrahend ist gleich Minuend minus Differenz
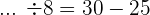
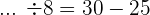
Wir subtrahieren
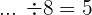
Dividend ist gleich Divisor geteilt durch Quotient

Berechne die folgenden Operationen auf zwei verschiedene Arten:
a 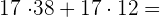
b 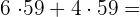
c 
Berechne die folgenden Operationen auf zwei verschiedene Arten:
Lösung:
a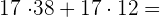
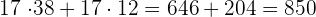
Wir klammern den gemeinsamen Faktor aus
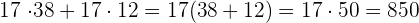
b 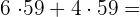
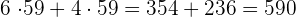
Wir klammern den gemeinsamen Faktor aus
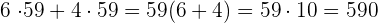
c 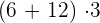

Wir wenden das Distributivgesetz an

Gemeinsamen Faktor ausklammern:
a 
b 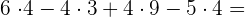
c 
Gemeinsamen Faktor ausklammern:
Lösung:
a 
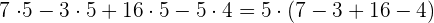
b 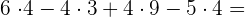
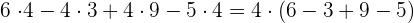
c 

Drücke als Potenzen aus:
a 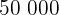
b 
c 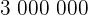
Drücke in Potenzen aus: Lösung:Wir nehmen die Zahl ohne die Nullen und multiplizieren sie mit  hoch die Anzahl der Nullen.
hoch die Anzahl der Nullen.
a 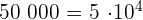
b 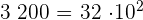
c 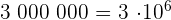
Schreibe als eine Potenz:
a 
b 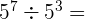
c 
d 
e 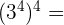
f 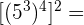
g 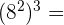
h 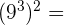
i 
j 
k 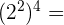
l 
m 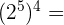
n 
o 
p 
Schreibe als eine Potenz:
Lösung:
a 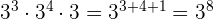
b 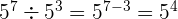
c 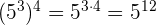
e 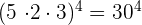
e 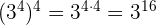
f 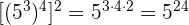
g 
h 
i 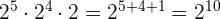
j 
k 
l 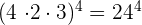
m 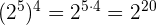
n 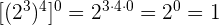
o
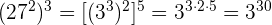
p 
Verwende Potenzen, um die Polynomzerlegung dieser Zahlen durchzuführen:
a 
b 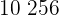
c 
Verwende Potenzen, um die Polynomzerlegung dieser Zahlen durchzuführen:
Lösung:
a 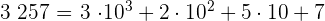
b 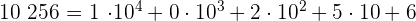
c 
Berechne die Wurzeln:
a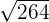
b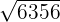
c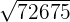
Berechne die Wurzeln: Lösung:a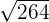
Wir unterteilen die Zahlen in zwei Gruppen, beginnend auf der rechten Seite
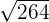
Mit der ersten Ziffer  berechnen wir die Zahl, die nach dem Quadrat der vorgegebenen Zahl am nächsten kommt
berechnen wir die Zahl, die nach dem Quadrat der vorgegebenen Zahl am nächsten kommt
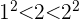 , weshalb wir
, weshalb wir  nehmen
nehmen
Diese Zahl  schreiben wir in das Kästchen. Sie wird die 1. Ziffer der Wurzel sein
schreiben wir in das Kästchen. Sie wird die 1. Ziffer der Wurzel sein
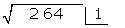
Das Quadrat der erhaltenen Zahl 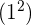 wird von der 1. Ziffer subtrahiert
wird von der 1. Ziffer subtrahiert
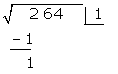
Hinter den Rest setzen wir die nächste Zifferngruppe des Radikanden  , trennen die Zahl der 1. Ziffer nach rechts ab
, trennen die Zahl der 1. Ziffer nach rechts ab  und teilen den Rest
und teilen den Rest  durch das Doppelte der Zahl, die wir im Kästchen haben
durch das Doppelte der Zahl, die wir im Kästchen haben 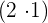
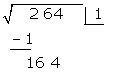
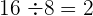
Unter das Kästchen kommt ein weiteres Kästchen mit dem erhaltenen Doppelten 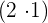 , gefolgt vom Quotienten der Division
, gefolgt vom Quotienten der Division 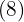 und die gebildete Zahl wird mit dem erhaltenen Quotienten
und die gebildete Zahl wird mit dem erhaltenen Quotienten 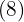 multipliziert
multipliziert
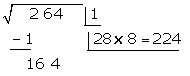
Da diese Zahl größer ist als der Rest  , müssen wir es mit kleineren Zahlen versuchen, bis das Produkt kleiner ist als der Rest
, müssen wir es mit kleineren Zahlen versuchen, bis das Produkt kleiner ist als der Rest
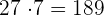
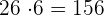
Mit  ist das erhaltene Ergebnis kleiner als der Rest, also setzen wir
ist das erhaltene Ergebnis kleiner als der Rest, also setzen wir  als zweite Ziffer der Wurzel ein
als zweite Ziffer der Wurzel ein
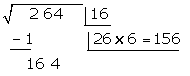
Wir subtrahieren das erhaltene Produkt 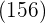 vom Rest
vom Rest 
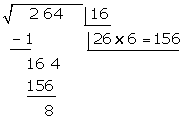
 ist die Wurzel und
ist die Wurzel und  ist der Rest
ist der Rest
Wir überprüfen das Ergebnis, indem wir die Probe machen
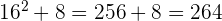
b 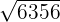
Wir unterteilen die Zahlen in zwei Gruppen, beginnend auf der rechten Seite
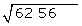
Mit den ersten beiden Ziffern 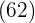 berechnen wir die Zahl, die zum Quadrat am nächsten kommt
berechnen wir die Zahl, die zum Quadrat am nächsten kommt
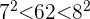 , weshalb wir
, weshalb wir  nehmen
nehmen
Diese Zahl  schreiben wir in das Kästchen. Sie wird die 1. Ziffer unter der Wurzel sein
schreiben wir in das Kästchen. Sie wird die 1. Ziffer unter der Wurzel sein
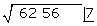
Das Quadrat der erhaltenen Zahl 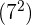 wird von der Gruppe der ersten zwei Ziffern subtrahiert
wird von der Gruppe der ersten zwei Ziffern subtrahiert
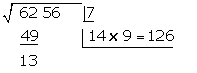
Hinter den Rest setzen wir die nächste Zifferngruppe des Radikanden  , trennen die von der ersten Ziffer gebildete Zahl nach rechts
, trennen die von der ersten Ziffer gebildete Zahl nach rechts  und teilen den Rest
und teilen den Rest 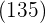 durch das Doppelte der Zahl, die wir im Kästchen haben
durch das Doppelte der Zahl, die wir im Kästchen haben 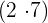
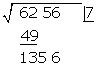
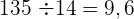 . Wir probieren mit
. Wir probieren mit 
Unter das Kästchen kommt ein weiteres Kästchen mit dem erhaltenen Doppelten 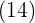 , gefolgt vom Quotienten der Division
, gefolgt vom Quotienten der Division 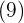 und die gebildete Zahl wird mit dem erhaltenen Quotienten
und die gebildete Zahl wird mit dem erhaltenen Quotienten 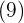 multipliziert
multipliziert
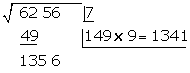
Wir subtrahieren das erhaltene Produkt 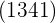 vom Rest
vom Rest 
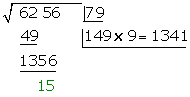
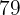 ist die Wurzel und
ist die Wurzel und  ist der Rest
ist der Rest
Wir überprüfen das Ergebnis, indem wir die Probe machen

c 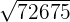
Wir unterteilen die Zahlen in zwei Gruppen, beginnend auf der rechten Seite
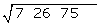
Mit der ersten Ziffer  berechnen wir die Zahl, die zum Quadrat der vorgegebenen Zahl am nächsten kommt
berechnen wir die Zahl, die zum Quadrat der vorgegebenen Zahl am nächsten kommt
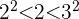 , weshalb wir
, weshalb wir  nehmen
nehmen
Diese Zahl  schreiben wir in das Kästchen. Sie wird die erste Ziffer der Wurzel sein
schreiben wir in das Kästchen. Sie wird die erste Ziffer der Wurzel sein
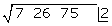
Das Quadrat der erhaltenen Zahl 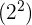 subtrahieren wir von der 1. Ziffer
subtrahieren wir von der 1. Ziffer
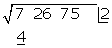
Hinter den Rest schreiben wir die nächste Zifferngruppe des Radikanden  und trennen die 1. Ziffer von der Zahl
und trennen die 1. Ziffer von der Zahl  ab. Wir dividieren den Rest
ab. Wir dividieren den Rest  durch das Doppelte der Zahl, die in unserem Kästchen steht
durch das Doppelte der Zahl, die in unserem Kästchen steht 
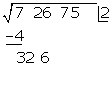
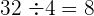
Unter das Kästchen kommt ein weiteres Kästchen mit dem erhaltenen Doppelten  , gefolgt vom Quotienten der Division
, gefolgt vom Quotienten der Division 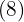 und die gebildete Zahl wird mit dem erhaltenen Quotienten
und die gebildete Zahl wird mit dem erhaltenen Quotienten 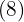 multipliziert
multipliziert
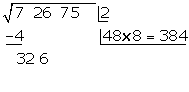
Da diese Zahl größer ist als der Rest 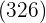 , müssen wir kleinere Zahlen ausprobieren, bis das Produkt kleiner ist als der Rest
, müssen wir kleinere Zahlen ausprobieren, bis das Produkt kleiner ist als der Rest
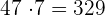
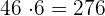
Mit  ist das erhaltene Ergebnis kleiner als der Rest, also stellen wir
ist das erhaltene Ergebnis kleiner als der Rest, also stellen wir  an die 2. Stelle der Wurzel
an die 2. Stelle der Wurzel
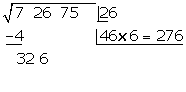
Wir subtrahieren das erhaltene Produkt 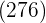 vom Rest
vom Rest 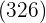
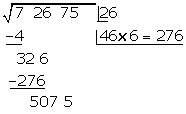
Hinter den Rest schreiben wir die nächste Zifferngruppe des Radikanden  und trennen die 1. Ziffer von der Zahl
und trennen die 1. Ziffer von der Zahl  ab. Wir dividieren den Rest
ab. Wir dividieren den Rest 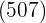 durch das Doppelte der Zahl, die in unserem Kästchen steht
durch das Doppelte der Zahl, die in unserem Kästchen steht 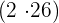
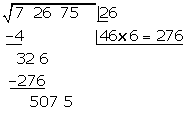
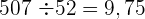 Wir probieren mit
Wir probieren mit 
Unter das Kästchen kommt ein weiteres Kästchen mit dem erhaltenen Doppelten  , gefolgt vom Quotienten der Division
, gefolgt vom Quotienten der Division 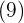 und die gebildete Zahl wird mit dem erhaltenen Quotienten
und die gebildete Zahl wird mit dem erhaltenen Quotienten 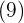 multipliziert
multipliziert
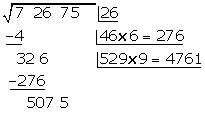
Da  kleiner ist als der Rest, stellen wir
kleiner ist als der Rest, stellen wir  an die 3. Stelle der Wurzel
an die 3. Stelle der Wurzel
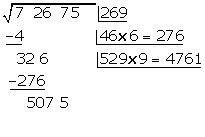
Wir subtrahieren das erhaltene Produkt 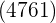 vom Rest
vom Rest 
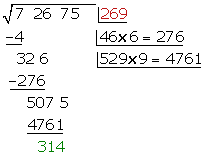
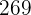 ist die Wurzel und
ist die Wurzel und 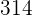 ist der Rest
ist der Rest
Wir überprüfen das Ergebnis, indem wir die Probe machen

Führe die folgenden kombinierten Rechenoperationen unter Berücksichtigung ihrer Rangfolge durch:
a 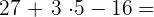
b
c 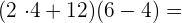
d 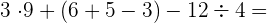
e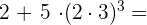
f 
g 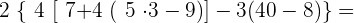
h 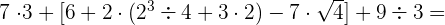
Führe die folgenden kombinierten Vorgänge unter Berücksichtigung ihrer Rangfolge durch:Lösung: a 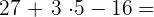
Wir multiplizieren
= 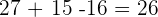
b 
Wir führen die Division durch
= 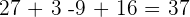
c 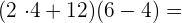
Wir führen das Produkt in der 1. Klammer und die Subtraktion in der 2. Klammer aus.
= 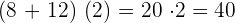
d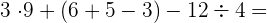
Wir führen das Produkt aus, rechnen innerhalb der Klammer und dividieren
= 
e 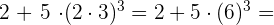
Wir multiplizieren innerhalb der Klammer und nehmen das Ergebnis hoch 3
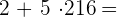
Wir führen das Produkt aus
= 
f 
Wir führen die Berechnungen innerhalb der Klammer aus
= 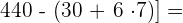
Wir multiplizieren
= 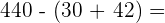
Wir rechnen innerhalb der Klammer
= 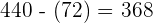
g 
Wir multiplizieren in der 1. Klammer und subtrahieren davon  .
.
Und nun die 2. Klammer
= 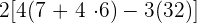 =
=
Wir multiplizieren
= 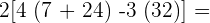
Wir addieren in der 1. Klammer
= 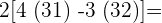
Wir führen die beiden Multiplikationen der eckigen Klammern durch
= 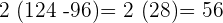
h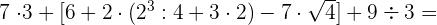
Wir führen die angegebenen Multiplikationen und Divisionen durch
Im Falle der Potenz müssen wir zur 3. Potenz erheben und dann durch  dividieren
dividieren
Wir lösen die Wurzel und multiplizieren mit 
= 
Wir addieren in der Klammer
= 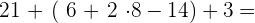
Wir multipizieren
= 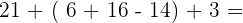
Wir berechnen innerhalb der Klammer
= 


