Kapitel
- Definition und Klassifizierung von ganzen Zahlen
- Betrag einer ganzen Zahl
- Hierarchie der Rechenoperationen
- Addition von ganzen Zahlen und Rechenregeln
- Subtraktion von ganzen Zahlen und Rechenregeln
- Multiplikation von ganzen Zahlen und Rechenregeln
- Division von ganzen Zahlen und Rechenregeln
- Potenzen ganzer Zahlen und Rechenregeln
- Aufgaben mit Potenzen
- Aufgaben mit Lösungen zu ganzen Zahlen

Definition und Klassifizierung von ganzen Zahlen
Die Menge ganzer Zahlen wird gebildet durch:

Das heißt, die natürlichen Zahlen, ihre Gegenzahlen (negative Zahlen) und die Null.
Sie werden in drei Teile eingeteilt:
- ganze positive Zahlen oder natürliche Zahlen
- ganze negative Zahlen
- Null
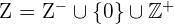
Da die ganzen Zahlen die positiven ganzen Zahlen enthalten, werden die natürlichen Zahlen als eine Teilmenge der ganzen Zahlen betrachtet:  .
.
Wie nachstehend dargestellt,
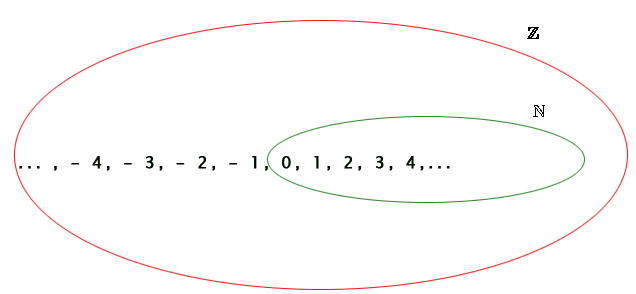
Betrag einer ganzen Zahl
Der Betrag einer ganzen Zahl ist die natürliche Zahl, die sich ergibt, wenn ihr Vorzeichen wegfällt, d. h,
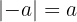
und
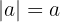
El valor absoluto de un número se puede considerar como su distancia desde cero.
Hierarchie der Rechenoperationen
1 Wir führen die Berechnungen innerhalb runder, eckiger und geschweifter Klammern durch.
2 Wir berechnen Potenzen und Wurzeln.
3 Wir multiplizieren und dividieren.
4 Wir addieren und subtrahieren.
Addition von ganzen Zahlen und Rechenregeln
Im Folgenden wird die Addition ganzer Zahlen anhand ihrer Eigenschaften veranschaulicht:
1Intern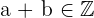
Beispiel:

2Assoziativ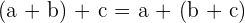
Beispiel:
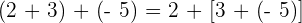

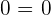
3Kommutativ
Beispiel:
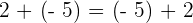
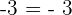
4Neutrales Element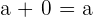
Beispiel:

5Gegenelement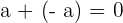
Beispiel:

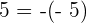
Beispiele für Probleme mit ganzen Zahlen
1 Wenn die zu addierenden Zahlen das gleiche Vorzeichen haben, werden die Beträge addiert und das gemeinsame Vorzeichen wird zum Ergebnis hinzugefügt.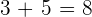

2 Wenn die Summanden unterschiedliche Vorzeichen haben, werden die Beträge subtrahiert (der größere Wert wird vom kleineren subtrahiert) und das Ergebnis erhält das Vorzeichen der größeren Zahl.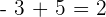
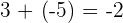
Subtraktion von ganzen Zahlen und Rechenregeln
Subtraktion ganzer Zahlen
Die Differenz der ganzen Zahlen erhält man, indem man das Gegenteil des Subtrahenden zum Minuenden addiert.
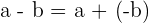
Beispiel:
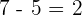

Rechenregeln für ganze Zahlen
1Intern
Beispiel:
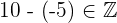
2Nicht kommutativ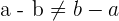
Beispiel:
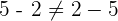
Multiplikation von ganzen Zahlen und Rechenregeln
Multiplikation von ganzen Zahlen
Die Multiplikation mehrerer ganzer Zahlen ergibt eine weitere ganze Zahl, die als Betrag das Produkt der Beträge und als Vorzeichen das Vorzeichen hat, das sich aus der Anwendung der Vorzeichenregel ergibt.
Vorzeichenregel
Bei der Multiplikation müssen die folgenden Vorzeichenregeln beachtet werden:
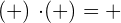

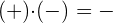

Beispiel: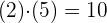
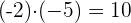

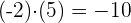
Eigenschaften der Multiplikation ganzer Zahlen
1Intern
Beispiel:
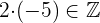
2Assoziativ
Beispiel:

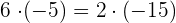
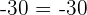
3Kommutativ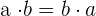
Beispiel:

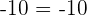
4Neutrales Element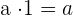
Beispiel:

5Distributiv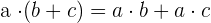
Beispiel:
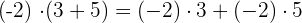
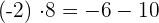
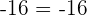
6Gemeinsamen Faktor ausklammern
Beispiel:

Division von ganzen Zahlen und Rechenregeln
Division von ganzen Zahlen
Die Division zweier ganzer Zahlen ergibt eine weitere ganze Zahl, die als Betrag den Quotienten der beiden Beträge und als Vorzeichen das durch Anwendung der Vorzeichenregel erhaltene Vorzeichen hat.

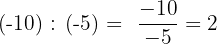
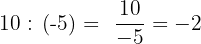
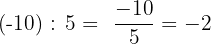
Eigenschaften der Division ganzer Zahlen
1Es handelt sich nicht um eine interne Rechenoperation
Beispiel:
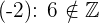
2Nicht kommutativ
Beispiel:
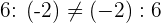
Potenzen ganzer Zahlen und Rechenregeln
Potenzen ganzer Zahlen
Die Potenz des natürlichen Exponenten einer ganzen Zahl ergibt eine weitere ganze Zahl, deren Betrag dem Betrag der Potenz entspricht und deren Vorzeichen dasjenige ist, das sich aus der Anwendung der folgenden Regeln ergibt:
1Potenzen mit geradem Exponenten sind immer positiv.
2 Potenzen mit ungeradem Exponenten haben dasselbe Vorzeichen wie die Basis.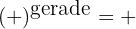
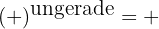
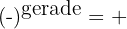
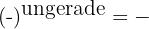
Eigenschaften von Potenzen ganzer Zahlen
1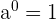
2 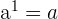
3 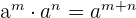
Beispiel: 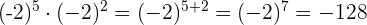
4 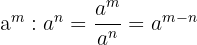
Beispiel: 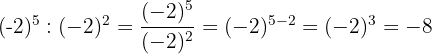
5 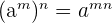
Beispiel: 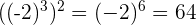
6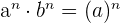
Beispiel: 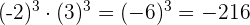
7
Beispiel: 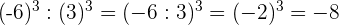
8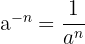 si
si 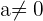
Beispiel: 
Aufgaben mit Potenzen





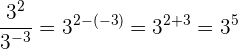
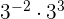


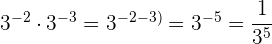
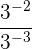

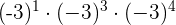
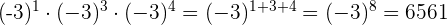
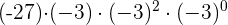

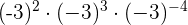

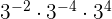
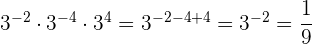


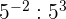
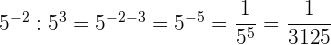
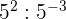


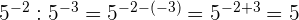
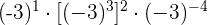

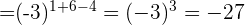
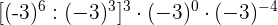
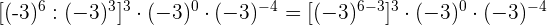
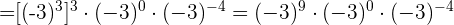

Aufgaben mit Lösungen zu ganzen Zahlen
Führe die folgenden Operationen mit ganzen Zahlen durch
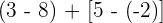
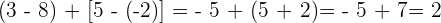
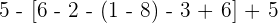
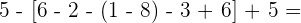
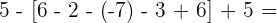
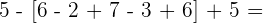
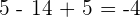
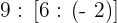

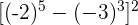

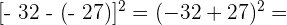

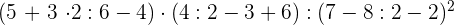
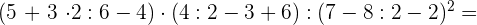


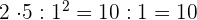
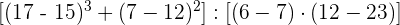

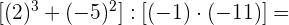




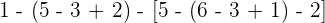
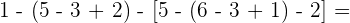
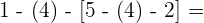

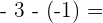
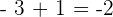
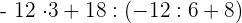

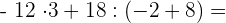

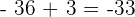
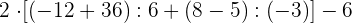
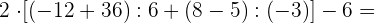

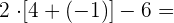
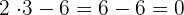

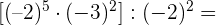
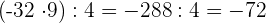
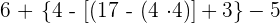
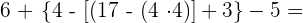
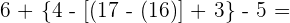

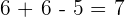
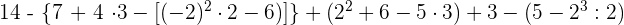
Zuerst führen wir die Potenzen, Produkte und Quotienten aus den Klammern aus. 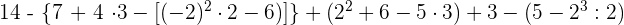

Wir rechnen mit den Produkten und Quotienten der Klammern.
Wir rechnen die Summen und Differenzen der Klammern aus.
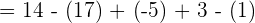
Die Beseitigung von Klammern muss unter Berücksichtigung folgender Tatsache erfolgen:
Wenn der Klammer das Zeichen + vorangestellt ist, werden die darin enthaltenen Terme unter Beibehaltung ihres Vorzeichens entfernt. Steht vor der Klammer das Zeichen - , so muss das Vorzeichen aller Terme in der Klammer geändert werden, wenn die Klammer entfernt wird.
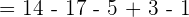

Mit KI zusammenfassen:












