Kapitel
Die ganzen Zahlen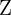 
sind die Menge der Zahlen, die aus den natürlichen Zahlen (auch positive ganze Zahlen genannt), ihren Gegenzahlen (negative ganze Zahlen) und der Null bestehen. Die ganzen Zahlen sehen wie folgt aus:
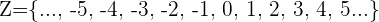
Ordnung der ganzen Zahlen
Die ganzen Zahlen sind in aufsteigender Reihenfolge geordnet. Die Kriterien zur Bestimmung der Reihenfolge einer Teilmenge von ganzen Zahlen sind wie folgt:
1 Jede negative Zahl ist kleiner als 0. Das heißt: Wenn 
eine negative ganze Zahl ist, ist 
.
2 Jede positive Zahl ist größer als 0. Das heißt: Wenn eine positive ganze Zahl ist, ist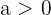 
.
3 Von zwei positiven ganzen Zahlen ist diejenige mit dem größeren Betrag größer. Das heißt: Wenn und 
positive ganze Zahlen sind, die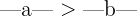 
erfüllen, ist 
.
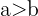Zum Beispiel: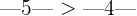 
bedeutet, dass 
.
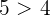4 Von zwei negativen ganzen Zahlen ist diejenige mit dem kleineren Betrag größer. Das heißt: Wenn und negative ganze Zahlen sind, die 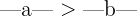erfüllen, ist 
.
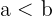Zum Beispiel: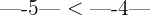 
bedeutet, dass 
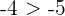. Je weiter rechts sich also eine Zahl auf der Zahlengeraden befindet, desto größer ist sie.
Addition von ganzen Zahlen
1 Wenn die Summanden das gleiche Vorzeichen haben, werden die Beträge addiert und das Ergebnis erhält das gemeinsame Vorzeichen.
Zum Beispiel: 
und 
haben das gleiche Vorzeichen. Es wird also die Summe der Beträge berechnet und das Vorzeichend der beiden Zahlen zugewiesen, d. h.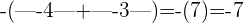 
.
2 Wenn die Summanden unterschiedliche Vorzeichen haben, werden die Beträge subtrahiert (der größere Wert wird vom kleineren subtrahiert), und das Ergebnis erhält das Vorzeichen der Zahl mit dem größeren Betrag.
Zum Beispiel: und 
haben unterschiedliche Vorzeichen. Es wird also die Differenz der Beträge berechnet und das Vorzeichen der Zahl mit dem größeren Betrag zugewiesen, d. h. 
.
Regeln für die Addition
Wenn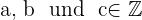 
, gelten folgende Regeln:
1. Intern:
2. Assoziativ:
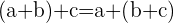
3. Kommutativ:
4. Neutrales Element:
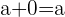
5. Addition mit Gegenzahl
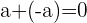
Subtraktion von ganzen Zahlen
Die Differenz von ganzen Zahlen erhält man, indem man den Minuenden mit der Gegenzahl des Subtrahenden addiert.
Regeln für die Subtraktion
1. Intern:
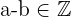
2. Nicht kommutativ:
Wir stellen fest, dass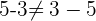 
Multiplikation von ganzen Zahlen
Das Produkt aus mehreren ganzen Zahlen ist eine weitere ganze Zahl, die als Betrag das Produkt der Beträge und als Vorzeichen das durch Anwendung der Vorzeichenregel erhaltene Vorzeichen hat.
Vorzeichenregel
- Das Produkt der Multiplikation zweier Zahlen mit gleichem Vorzeichen ist immer positiv:
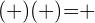
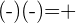
- Das Produkt der Multiplikation zweier Zahlen mit unterschiedlichen Vorzeichen ist immer negativ:
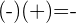
Regeln für die Multiplikation
1. Intern:
2. Assoziativ:
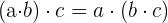
3. Kommutativ:
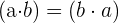
4. Multiplikation mit neutralem Element
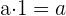
5. Distributiv:
6. Gemeinsamen Faktor ausklammern:
Dies ist die Umkehrung des Distributivgesetzes.
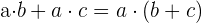
Division von ganzen Zahlen
Der Quotient zweier ganzer Zahlen ist eine weitere Zahl, die als Betrag den Quotienten der Beträge und als Vorzeichen das Vorzeichen hat, das sich aus der Anwendung der Vorzeichenregel ergibt.
Regeln für die Division
1. Nicht intern:
Wir stellen fest, dass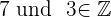 
. Jedoch ist 
keine ganze Zahl.
2. Nicht kommutativ.
Potenzen mit ganzzahligem Exponenten
Si Wenn der Exponent eine natürliche Zahl 
ist, dann gibt dies an, wie oft die Basis mit sich selbst multipliziert wird. Zum Beispiel:
Vorzeichenregel für Potenzen
- Ganze Zahlen zu einer beliebigen Potenz sind immer positiv:
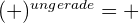
- Wenn eine negative Zahl auf eine Potenz erhöht wird, hängt das Vorzeichen des resultierenden Wertes davon ab, ob die Potenz eine gerade oder eine ungerade Zahl ist:
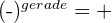
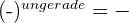
Regeln für Potenzen
1. Zahlen zur Potenz 0:
·
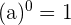2. Zahlen zur Potenz 1:
·
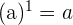3. Produkt aus Potenzen mit gleicher Basis:
.
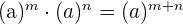4. Division von Potenzen mit gleicher Basis:
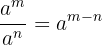
5. Potenz einer Potenz:
.
6. Produkt aus Potenzen mit gleichem Exponenten:
.
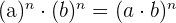7. Division von Potenzen mit gleichem Exponenten:
.
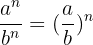8. Potenzen mit negativem ganzzahligen Exponenten
Potenzen mit negativem Exponenten werden wie folgt dargestellt:
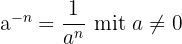
Potenzen mit negativen Exponenten ergeben im Allgemeinen keine ganze Zahl.
Wurzeln
Eine Wurzel ist ein Ausdruck der Form 
, wobei 
und 
. Außerdem ist der Radikand und der Wurzelexponent. Damit die Rechenoperation innerhalb der reellen Zahlen gültig ist, wenn negativ ist, muss ungerade sein. Im Allgemeinen ist die Wurzel aus einer natürlichen Zahl keine ganze Zahl.
Quadratwurzel
Die Quadratwurzel ist die Umkehrung des Quadrierens. Die Quadratwurzel einer natürlichen Zahl ist exakt, vorausgesetzt, der Radikand ist ein perfektes Quadrat (eine Zahl ist ein perfektes Quadrat, wenn bei der Zerlegung in ihre Primfaktoren jeder der Terme auf eine gerade Potenz erhöht wird).
Einige Beispiele:
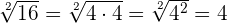
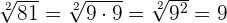
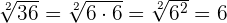
Reihenfolge von Rechenoperationen
Bei der Durchführung einer Reihe von mehreren Rechenoperationen muss die unten dargestellte Reihenfolge der Rechenoperationen beachtet werden:
1 Berechnungen innerhalb von runden, eckigen und geschweiften Klammern durchführen.
2 Potenzen und Wurzeln berechnen.
3 Multiplizieren und dividieren.
4 Addieren und subtrahieren.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
