Kapitel

Definition der natürlichen Zahlen
Die Menge der natürlichen Zahlen wird wie folgt gebildet:

Mit den natürlichen Zahlen zählen wir die Elemente einer Menge (Kardinalzahl). Oder wir drücken die Position oder Reihenfolge aus, die ein Element in einer Menge einnimmt (Ordnungszahl).
Die natürlichen Zahlen sind geordnet, so dass man zwei natürliche Zahlen vergleichen kann:
 ; 5 ist größer als 3.
; 5 ist größer als 3.
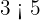 ; 3 ist kleiner als 5.
; 3 ist kleiner als 5.
Natürliche Zahlen sind unendlich. Wenn wir 1 zu einer natürlichen Zahl addieren, erhalten wir eine weitere natürliche Zahl.
Addition natürlicher Zahlen
a + b = c
Die Terme der Summe, a und b, werden als Summanden bezeichnet und das Ergebnis, c, als Summe.
Regeln für die Addition
1 Intern: 
Die Summe gehört zu den natürlichen Zahlen
2 Assoziativ: 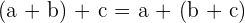
Die Summe aus zwei ersten Zahlen plus einer dritten ist gleich der Summe aus einer ersten Zahl plus der Summe der beiden letzten.
Beispiel
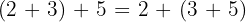
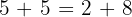
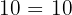
3 Kommutativ: 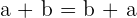
Die Reihenfolge der Addition hat keinen Einfluss auf das Ergebnis
Beispiel

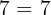
4 Neutrales Element: 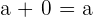
Das neutrale Element der Summe ergibt die gleiche Zahl, in diesem Fall 0.
Beispiel
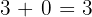
a - b = c
Die Terme, die an einer Subtraktion beteiligt sind, heißen: a, der Minuend, und b, der Subtrahend. Das Ergebnis, c, wird als Differenz bezeichnet.
Regeln für die Subtraktion
1Es handelt sich nicht um eine interne Rechenoperation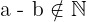
Die Subtraktion gehört nicht zu den natürlichen Zahlen, da das Ergebnis eine negative Zahl sein kann.
Beispiel
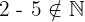
2Nicht kommutativ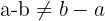
Die Reihenfolge, in der die Subtraktion durchgeführt wird, verändert das Ergebnis
Beispiel
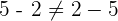
Multiplikation natürlicher Zahlen
a · b = c
Die Terme a und b werden als Faktoren bezeichnet, das Ergebnis, c, als Produkt.
Regeln für die Multiplikation
1 Intern: 
Das Produkt gehört zu den natürlichen Zahlen
2Assoziativ: 
Die Multiplikation der ersten beiden und dann einer dritten ist dasselbe wie die Multiplikation der ersten und dann der letzten beiden
Beispiel
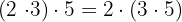
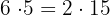
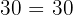
3Kommutativ: 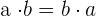
Die Reihenfolge, in der wir die Multiplikation durchführen, ändert nichts am Ergebnis
Beispiel

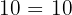
4Neutrales Element: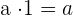
Das neutrale Element der Multiplikation ist die 1, denn es ist dasjenige, das den Ausgangswert liefert
Beispiel

5Distributiv: 
Die Multiplikation einer Zahl mit einer Summe wird aufgeteilt, d. h. die Zahl wird mit jedem Element der Summe multipliziert
Beispiel
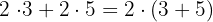
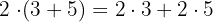
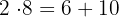

6Gemeinsamen Faktor ausklammern: 
Wenn es einen gemeinsamen Term in den Elementen der Summe gibt, kann er ausgeklammert werden
Beispiel
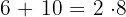

Division natürlicher Zahlen
D : d = c
Die an einer Division beteiligten Terme werden D, der Dividend und d, der Divisor genannt. Das Ergebnis, c, wird Quotient genannt.
Regeln für die Division
1Division ohne Rest
Die Division ist exakt, wenn der Rest bei der Durchführung der Rechenoperation gleich 0 ist.
Beispiel
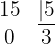

2Division mit Rest
Bei dieser Art von Division bleibt ein Rest
Beispiel

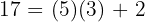
3Nicht intern
Die Division gehört nicht zu den natürlichen Zahlen, da wir Dezimalzahlen erhalten könnten.
Beispiel

4Nicht kommutativ: 
Die Reihenfolge der Rechenoperation verändert das Ergebnis.
Beispiel

50 geteilt durch eine beliebige Zahl ergibt 0.
Beispiel
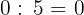
6Es kann nicht durch 0 dividiert werden.
Regeln für Potenzen
1 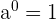
Eine Zahl hoch 0 ist 1.
2 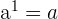
Eine Zahl hoch 1 ergibt dieselbe Zahl.
3 Produkt aus Potenzen mit gleicher Basis: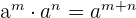
Bei einem Produkt mit gleicher Basis werden die Exponenten addiert.
Beispiel

4 Quotient aus Potenzen mit gleicher Basis :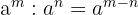
Bei einem Quotienten mit gleicher Basis werden die Exponenten subtrahiert.
Beispiel

5 Potenz einer Potenz:
Bei der Potenz einer Potenz werden die Exponenten multipliziert.
Beispiel

6 Produkt aus Potenzen mit gleichem Exponenten: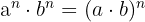
Das Produkt verschiedener Basen, die aber alle denselben Exponenten haben, ist gleich dem Produkt der Basen, das auf den Exponenten erhöht wird.
Beispiel
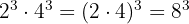
7 Quotient aus Potenzen mit gleichem Exponenten: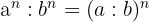
Der Quotient verschiedener Basen, die aber alle denselben Exponenten haben, ist gleich dem Quotienten der Basen, der auf den Exponenten erhöht wird.
Beispiel
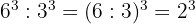
Aufgaben zu Potenzen
1 
2 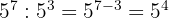
3 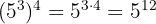
4 
5 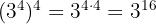
6 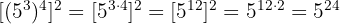
7 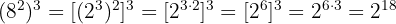
8 
9 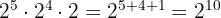
10 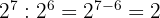
11 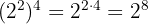
12 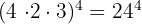
13 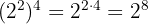
14 
15 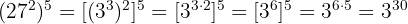
16 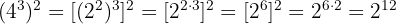
Eigenschaften von Wurzeln
1 Exakte Wurzel: Radikand= 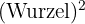
Von einer exakten Wurzel spricht man, wenn man eine Zahl findet, die mit sich selbst multipliziert den Radikanden ergibt.
Beispiel
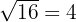

2 Nicht exakte Wurzel: <Radikand= (Wurzel)2 + Rest
Von einer ganzzahligen Wurzel spricht man, wenn eine Zahl gefunden werden kann, die, wenn sie mit sich selbst plus einer ganzen Zahl multipliziert wird, den Radikanden ergibt.
Beispiel
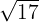

Reihenfolge von Rechenoperationen
1 Wir führen die Berechnungen innerhalb der operaciones entre runden, eckigen und geschweiften Klammern durch.
2 Potenzen und Wurzeln berechnen.
3 Multiplikation und Subtraktion.
4 Addition und Subtraktion.
Kombinierte Rechenoperationen ohne Klammern
1.1Kombination aus Addition und Subtraktion.
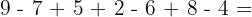
Von links beginnend, führen wir die Operationen aus, wie sie erscheinen.
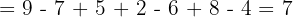
1.2 Kombination aus Addition, Subtraktion und Multiplikation.

Wir führen zuerst die Multiplikation durch, da sie die höchste Priorität hat.

Wir addieren und subtrahieren.
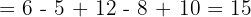
1.3 Kombination aus Addition, Subtraktion, Multiplikation und Division.

Wir führen die Multiplikation und die Division in der Reihenfolge aus, in der wir sie vorfinden, da die beiden Operationen die gleiche Priorität haben.
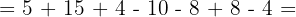
Wir addieren und subtrahieren.
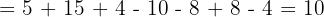
1.4 Kombination aus Addition, Subtraktion, Multiplikation, Division und Potenzen.
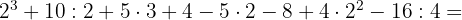
Wir führen die Potenzen zuerst aus, da sie die höchste Priorität haben.
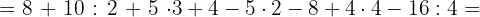
Wir multiplizieren und dividieren.

Wir addieren und subtrahieren.

Kombinierte Rechenoperationen mit Klammern
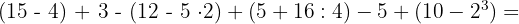
Wir führen zunächst die in den Klammern enthaltenen Rechenoperationen durch.
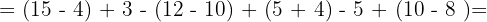
Wir eliminieren die Klammern, indem wir die entsprechenden Berechnungen durchführen.

Kombinierte Rechenoperationen mit Klammern
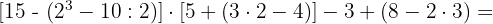
Zunächst rechnen wir mit den Potenzen, Produkten und Quotienten der Klammern.

Wir addieren und subtrahieren innerhalb der Klammern.

Anstelle von eckigen Klammern setzen wir direkt runde Klammern:

Wir rechnen innerhalb der Klammern.

Wir multiplizieren.

Wir addieren und subtrahieren.
= 83
Aufgaben und Problemstellungen mit Lösungen zu natürlichen Zahlen
1 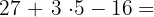
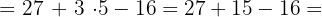 26
26
2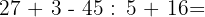
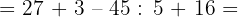 37
37
3 
 40
40
4 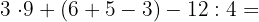
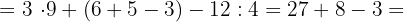 32
32
5 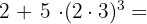
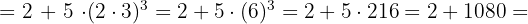 1082
1082
6 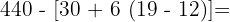
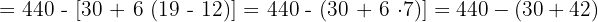
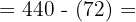 368
368
7 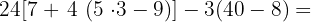
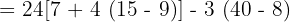
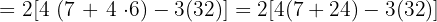
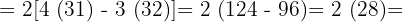 56
56
8 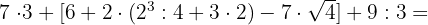
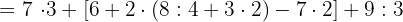
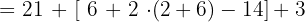
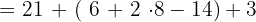

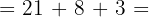 32
32
Mit KI zusammenfassen:












